Antécédent (mathématiques) - Définition

Définition

En mathématiques, étant donnés deux ensembles non vides E, F et une application , on appelle antécédent (par f) d'un élément y de F tout élément x de E tel que .

Un antécédent est donc, par définition, un élément de l'image réciproque .

Exemples

• Soient la fonction 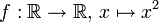et y un réel.

Si y > 0, y admet deux antécédents, qui son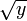t et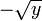

Si y = 0, y admet un seul antécédent, qui est 0

Si y < 0, y n'admet aucun antécédent

• Soient E un ensemble non vide, et une application 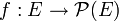, où 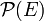désigne l'ensemble des parties de E. On définit  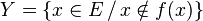: Y est une partie de E, autrement dit un élément de l'ensemble .
  

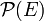Cet élément n'admet aucun antécédent par f. En effet, supposons qu'un tel antécédent 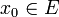existe. On a donc .

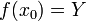Deux cas sont possibles :

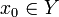, ce qui veut dire (par définition de Y) que 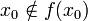, ou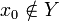

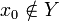, ce qui veut dire (par définition de Y) que 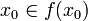, ou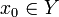

Dans les deux cas, on aboutit à une contradiction, ce qui prouve par l'absurde que Y n'a pas d'antécédent (cf. l'argument de la diagonale de Cantor).

Image d'un ensemble par une application

Soient une application et A un sous-ensemble de E. On appelle image de A par f l'ensemble des éléments y de F qui admettent au moins un antécédent appartenant à A ; on la note :

.

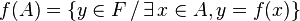En particulier, l'image de E par f, appelée image de f, est l'ensemble des éléments y de F qui admettent au moins un antécédent :

.

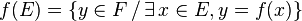Injections, surjections, bijections

Soit une application .

• On dit que f est injective, ou que c'est une injection, si tout élément de F admet au plus un antécédent.
• On dit que f est surjective, ou que c'est une surjection, si tout élément de F admet au moins un antécédent, c'est-à-dire si

.

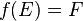• On dit que f est bijective, ou que c'est une bijection, si tout élément de F admet un antécédent et un seul, c'est-à-dire si f est à la fois injective et surjective.

Dans ce cas, on peut définir l'application 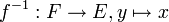, où x est l'unique antécédent de y par f. C'est aussi une bijection, dite réciproque de f.

(l'exemple vu plus haut montre qu'il n'existe aucune application surjective ).