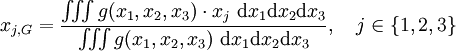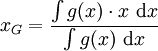Le barycentre (Le barycentre est un point (Graphie) mathématique (géométrie analytique) construit à partir d'un ensemble (En théorie des ensembles, un ensemble, désigne intuitivement une collection d’objets (que l'on appelle éléments...) d'autres. Il correspond) est un point mathématique (Les mathématiques désignent la science du vrai et du faux en général. C'est-à-dire qu'elle ne s'attache pas à dire ce...) (géométrie analytique) construit à partir d'un ensemble d'autres. Il correspond

• en statistiques à la notion de moyenne (Il y a plusieurs façon de calculer une moyenne d'un ensemble de nombres. Celle qu'il convient de retenir dépend de la...) (ou espérance),
• en physique (La physique (du grec φυσικη) est étymologiquement la science de la nature. Son champ...) (cinématique, mécanique (Dans le langage courant, la mécanique est le domaine des machines, moteurs, véhicules, organes (engrenages, poulies,...) du point) à la notion de centre d'inertie (L'inertie d'un corps découle de la nécessité d'exercer une force (Le mot force peut désigner un pouvoir mécanique sur les choses, et aussi, métaphoriquement, un pouvoir de la volonté ou...) sur celui-ci pour modifier sa vitesse (La vitesse est une grandeur physique qui permet d'évaluer l'évolution d'une quantité en fonction du temps.) (vectorielle)....) (ou centre de masse (La masse est une propriété fondamentale de la matière qui se manifeste à la fois par l'inertie des corps et leur...)) ou de centre de gravité (La gravitation est une des quatre interactions fondamentales de la physique.),
• et en mécanique du solide à la notion de moment (moment d'inertie, moment cinétique),
• en analyse spatiale au point moyen ou point central.

On utilise également ce concept pour la construction de courbes de Bézier.

Un peu d'histoire

En physique

Le barycentre de barus (poids) et centre est initialement le centre des poids (Le poids d'un corps nu ou force de pesanteur est la force exercée sur un corps (de masse m) immobile dans le...). C'est donc une notion physique et mécanique. Le premier à avoir étudié le barycentre en tant que centre des poids (ce qu'on appelle de nos jours (Le jour ou la journée est l'intervalle qui sépare le lever du coucher du Soleil ; c'est la période entre deux...) le centre de gravité) est le mathématicien et physicien Archimède. Il est un des premiers à comprendre et expliciter le principe des moments, le principe des leviers et le principe du barycentre. Il écrit dans son traité Sur le centre de gravité de surface (Il existe de nombreuses acceptions au mot surface, parfois objet géométrique, parfois frontière physique, souvent...) plane (La plane est un outil pour le travail du bois. Elle est composée d'une lame semblable à celle d'un couteau, munie de...):

« Tout corps pesant a un centre de gravité bien défini en lequel tout le poids du corps peut être considéré comme concentré. » 

Son principe des moments et des leviers lui permet de construire assez simplement le barycentre O de deux points de masses m₁ et m₂ différentes.

Pour que la balance soit en équilibre, il faut que les moments et soient égaux. Si par exemple la masse m₁ est 4 fois plus importante que la masse m₂, il faudra que la longueur (La longueur d’un objet représente la distance entre deux de ses extrémités, les plus éloignées possibles. Lorsque...) OA soit 4 fois plus petite que la longueur OB. Cette condition se traduit de nos jours par l'égalité vectorielle

C'est le premier à avoir cherché des centres de gravité de surface comme des demi-disques, des paraboles. Il procède par approximations successives et a pu prouver que la recherche (La recherche scientifique désigne en premier lieu l’ensemble des actions entreprises en vue de produire et de...) d'un centre de gravité utilise des méthodes analogues à celle du calcul d'aire. Son travail est prolongé par celui de Paul Guldin (1635/1640) dans son traité Centrobaryca et celui de Leibniz à qui l'on doit la fonction vectorielle de Leibniz.

La notion de centre d'inertie G pour un système non solide est une notion dégagée par Christiaan Huygens (1654), lors de l'établissement de sa théorie des chocs : même s'il sait que P = P₀, il n'est pas évident pour lui que G ira à vitesse constante. En particulier au moment de la percussion, où des forces quasi-infinies entrent en jeu, avec éventuellement bris de la cible, G n'en continue pas moins imperturbé son mouvement : cela paraît mirifique à Huygens, qui ne connaît pas encore le calcul différentiel (Un différentiel est un système mécanique qui a pour fonction de distribuer une vitesse de rotation de façon adaptative...). C'est alors qu'il énonce le principe de mécanique :

« Le barycentre d'un système matériel se meut comme si toute la masse du système y était transportée, les forces extérieures du système agissant toutes sur ce barycentre. » 

On peut remarquer le glissement subtil entre barycentre, centre des poids (= centre de gravité) comme le voyait Archimède et barycentre, centre des masses (= centre d'inertie).

Autres champs d'application

Le barycentre, créé dans le cadre de la physique et de la mécanique, s'est vite révélé très utile dans bien d'autres domaines.

En géométrie (Selon la définition donnée par Euclide dans ses Éléments, la géométrie serait la science mathématique des figures dans...), il permet de repérer des points par rapport à d'autres points : ce sont les coordonnées barycentriques. C'est l'outil (Un outil est un objet finalisé utilisé par un être vivant dans le but d'augmenter son efficacité naturelle dans...) privilégié pour démontrer des alignements et des concours. On peut dire que la géométrie vectorielle (Cet article ou cette section doit être recyclé. Sa qualité devrait être largement améliorée en le réorganisant et en le...) est la géométrie des vecteurs et des combinaisons linéaires alors que la géométrie affine (La géométrie affine est la géométrie des espaces affines : il s'agit grossièrement d'ensembles de points définis...) est celle des points et des barycentres.

En statistique (La statistique (Une statistique (par opposition à la statistique) est, au premier abord, un nombre calculé à propos d'une population....) (par opposition à une statistique) est l'ensemble des instruments et de recherches mathématiques...), il permet le calcul et la représentation des moyennes pondérées. En probabilité (Probabilité vient du latin probare (prouver, ou tester). Le mot probable signifie « qui peut se produire »...), on le retrouve dans l'espérance mathématique (L'espérance mathématique est une valeur numérique permettant de mesurer le degré d'équité d'un jeu de hasard. Elle est...).

En logistique (La logistique est une activité de services qui a pour objet de gérer les flux de matières en mettant à disposition et...), c'est un outil puissant de décision.

En chimie (La chimie est la science qui étudie la composition et les réactions de la matière.), il permet de calculer la polarité d'une molécule.

Développement mathématique

Les mathématiques généralisent la construction d'Archimède du point d'équilibre de deux points affectés de deux masses positives progressivement à des ensembles plus complexes. Les coefficients peuvent être négatifs : Le barycentre des points A et B affectés des masses a et b (a + b non nul) est l'unique point G tel que

.

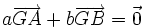Les coordonnées de G sont alors

Le nombre de points peut passer à trois points, quatre points et se généraliser à n points. Si la somme des masses a_i est non nulle, le barycentre du système est le point G tel que

.

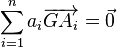Les coordonnées sont données (Dans les technologies de l'information (TI), une donnée est une description élémentaire, souvent codée, d'une chose,...) par les formules, pour j variant de 1 à la dimension (Dans le sens commun, la notion de dimension renvoie à la taille ; les dimensions d'une pièce sont sa longueur, sa...) de l'espace

C'est sous cette forme qu'il devient un outil puissant en géométrie affine.

Le nombre de points peut même devenir infini, permettant de trouver le barycentre d'une courbe (En géométrie, le mot courbe, ou ligne courbe désigne certains sous-ensembles du plan, de l'espace usuels. Par exemple,...) ou d'une surface.

Si l'ensemble constitue un domaine D continu, à chaque point M du domaine on affecte une densité (La densité est un nombre sans dimension, égal au rapport d'une masse d'une substance homogène à la masse du même volume...) g(M) où g est une fonction continue (un champ (Un champ correspond à une notion d'espace défini:) scalaire). Le barycentre est alors le point G tel que

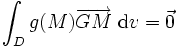dans l'espace ou 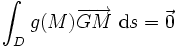dans le plan .

Si les points M ont pour coordonnées (x₁;x₂,x₃) la fonction de densité s'écrit g(x₁,x₂,x₃) et les coordonnées de G s'écrivent

Si l'on se ramène à une dimension, ou bien si l'on considère chaque coordonnée séparément, on retrouve la formule de la moyenne pondérée :

Développements physiques

Centre d'inertie

En mécanique, le centre d'inertie d'un corps correspond au barycentre des particules qui composent le corps en question ; chaque particule étant pondérée par sa masse propre. C'est donc le point par rapport auquel la masse est uniformément répartie.

Dans le cas d'un corps continu , on emploie comme fonction de pondération la masse volumique ρ du corps. Dans ce cas, la position du centre d'inertie G est défini par la relation suivante (O étant un point quelconque de l'espace) :

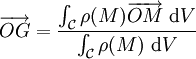ou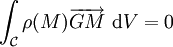

Le centre d'inertie ne dépend donc que de la masse volumique et de la forme du corps. C'est une caractéristique intrinsèque.

Une propriété étonnante du centre d'inertie est que son mouvement est parfaitement déterminé par les lois du mouvement, quoi qu'il arrive à ses composants aussi longtemps que ceux-ci ne subissent pas eux-mêmes de force nouvelle. Ainsi par exemple si un obus éclate en vol, le centre d'inertie de ses fragments continue à suivre imperturbablement une parabole (La parabole est l'intersection d'un plan avec un cône lorsque le plan est parallèle à l'une des génératrices du cône....) comme si de rien n'était (aux effets de résistance de l'air près) avant, pendant et après l'explosion (Une explosion est la transformation rapide d'une matière en une autre matière ayant un volume plus grand, généralement...). Attention : ceci ne s'applique évidemment pas à un obus balistique ou un astéroïde (Un astéroïde est un objet céleste dont la taille varie de quelques dizaines de mètres à plusieurs kilomètres de...), précisément parce que la force sur chaque éclat d'obus varie.

Centre de gravité

Le centre de gravité d'un corps correspond au barycentre des particules qui composent le corps en question ; chaque particule étant pondérée par son poids propre.

la position du centre de gravité G_g est défini par la relation suivante ( étant le champ de gravité au point M):

Il est à noter que le centre de gravité est fondamentalement lié au champ de gravité dans lequel le corps est plongé. Il n'existe pas forcément !

Très souvent en mécanique, la dimension des corps étant faible devant la rotondité de la terre (La Terre, foyer de l'humanité, est surnommée la planète bleue. C'est la troisième planète du système solaire en partant...), on considère un champ de gravité uniforme. Sous cette hypothèse, le centre de gravité et le centre d'inertie sont confondus.

Astronomie (Avec plus de 6 000 ans d'Histoire, l'astronomie est probablement la plus ancienne des sciences naturelles, ses origines...)

Animation (L'animation consiste à donner l'illusion du mouvement à l'aide d'une suite d'images. Ces images peuvent être dessinées,...) impliquant 2 corps de faible différence de masse. Le barycentre se trouve à l'extérieur du corps principal comme dans le cas du couple Pluton/Charon.

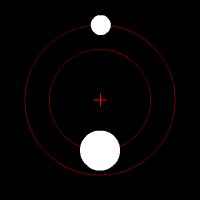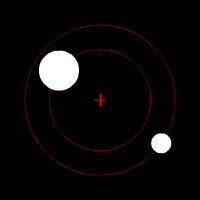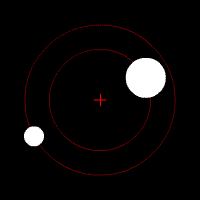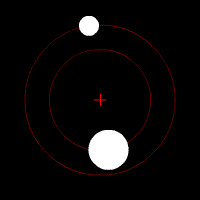
On parle de barycentre en ce qui concerne le couple formé par un corps stellaire possédant un satellite (Satellite peut faire référence à :). Le barycentre est le point autour duquel l'objet secondaire gravite. Si la plupart des couples connus possède leur barycentre à l'intérieur de l'objet principal, il existe des exceptions notables :

• Le cas du couple Pluton/Charon : la différence de masse entre ces deux corps est relativement faible, le barycentre se trouve donc à l'extérieur de Pluton (Pluton, dont la désignation officielle est (134340) Pluton, est la deuxième plus grande planète naine connue du système...). Pour certains astronomes, plutot que de parler de planètes et de satellites, il conviendrait dans ce cas précis de retenir la notion de « planète double ».
• Plusieurs astéroïdes reproduisent le cas de figure ci-dessus.
• Le barycentre du couple Jupiter/Soleil se trouve à l'extérieur de ce dernier à environ un rayon solaire (En astrophysique, le rayon solaire est l'unité de longueur conventionnellement utilisée pour exprimer la taille des...) de distance.
• On retrouve aussi cette particularité chez certaines étoiles doubles