Quantité de mouvement - Définition
En physique, la quantité de mouvement est la grandeur physique associée à la vitesse et la masse d'un objet. La quantité de mouvement d'un système fait partie, avec l'énergie, des valeurs qui se conservent lors des interactions entre éléments du système. Cette loi, d'abord empirique, a été expliquée par le théorème de Noether et est liée à la symétrie des équations de la physique par translation dans l'espace. Le terme anglais est momentum, et parfois on emploie le terme moment (ainsi le 4-moment en mécanique relativiste).
Quantité de mouvement en mécanique classique
En mécanique classique, la quantité de mouvement d'un point matériel de masse ![]() animé d'une vitesse
animé d'une vitesse ![]() , est définie comme produit de la masse et de la vitesse :
, est définie comme produit de la masse et de la vitesse :
![]()
C'est donc, comme la vitesse, une grandeur vectorielle.
L'unité SI de la quantité de mouvement est le kg . m . s-1.
Impulsion
La quantité de mouvement ne doit pas être confondue avec l'impulsion (faux-ami anglosaxon).
Une impulsion I modifie la quantité de mouvement. Une impulsion est calculée comme étant l'intégrale de la force en fonction de la durée.
ce qui, en utilisant la définition de la force, donne:
Quantité de mouvement d'un système : théorème du centre d'inertie
En mécanique classique, l'application des lois de Newton permet de démontrer le théorème du centre d'inertie qui apparaît comme la généralisation de la seconde loi de Newton pour un système quelconque (solide ou ensemble de points matériels, ensemble de solides) :
Si ![]() désigne la masse totale du système et G son centre d'inertie, alors, la quantité de mouvement du système est :
désigne la masse totale du système et G son centre d'inertie, alors, la quantité de mouvement du système est : ![]()
![]() désignant donc la vitesse du centre d'inertie du système et M la masse totale du système.
désignant donc la vitesse du centre d'inertie du système et M la masse totale du système.
Le théorème s'énonce alors ainsi : la variation de la quantité de mouvement du système est égale à la somme des forces extérieures s'exerçant sur le système : ![]()
Cette relation est évidemment fondamentale : c'est elle qui permet d'étudier le mouvement d'un solide sans avoir besoin de connaître les forces de liaison interatomique ! On peut ainsi aussi bien étudier la chute d'une pomme que le mouvement de la Lune autour de la Terre...
Un cas particulier important : si l'on imagine le choc de deux objets (ou particules) pour lequel les forces extérieures (au système constitué de ces 2 objets) est nulle (ou négligeable) alors la quantité de mouvement totale se conserve : elle est la même après le choc qu'avant le choc, et ce en dépit des interactions qui ont eu lieu pendant le choc. C'est d'ailleurs l'étude des chocs qui a conduit Descartes à penser qu'une certaine quantité du mouvement était nécessairement conservée...
En mécanique lagrangienne
En mécanique lagrangienne, si l'on note L(q,q') le lagrangien du système avec q la position et q' la vitesse du système, on a :
Quantité de mouvement en mécanique relativiste
Un aspect important de la quantité de mouvement est que l'on s'attend à ce qu'elle soit une grandeur conservée lors de transformations de translation. En effet, dans le cas contraire, cela impliquerait une modification sans cause de la position du centre de gravité d'un système de deux corps élastiques qui se percutent.
Aussi, lorsqu'Albert Einstein formula sa théorie de la relativité restreinte, il adapta la définition de la quantité de mouvement afin que celle-ci soit également conservée lors de transformations relativistes. La grandeur ainsi obtenue s'appele un 4-moment, c'est une grandeur vectorielle à quatre dimensions qui combine la quantité de mouvement classique et l'énergie et est définie de la façon suivante:
où:
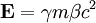 est l'énergie totale
est l'énergie totale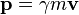 est la quantité de mouvement relativiste
est la quantité de mouvement relativiste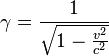 est un facteur appelé gamma relativiste
est un facteur appelé gamma relativiste- c est la vitesse de la lumière
La " LONGUEUR " de ce vecteur est la grandeur qui reste invariante lors de translation et est définie ainsi:
Les objets de masse nulle, tels que les photons, possèdent aussi un 4-moment la pseudo-norme de p est nulle : ![]()
Quantité de mouvement en mécanique quantique
En mécanique quantique, la quantité de mouvement est définie en tant qu'opérateur agissant sur la fonction d'onde. Le principe d'incertitude d'Heisenberg impose une limite sur la précision avec laquelle la quantité de mouvement et la position d'un système observable simple peuvent être simultanément connus.