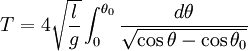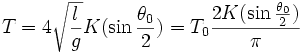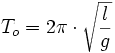Pendule pesant - Définition
On appelle pendule pesant tout solide mobile autour d'un axe (en principe horizontal) ne passant pas par son centre de gravité et placé dans un champ de pesanteur. Déplacé de sa position d'équilibre (stable) dans laquelle le centre de gravité est à la verticale de l'axe, le solide se met à osciller de part et d'autre de cette position dite d'équilibre. Un balancier d'horloge, une balançoire, etc, constituent des pendules pesants.
Le cas le plus simple est le pendule constitué d'un petit objet pesant accroché à un fil (ou une tige) de masse négligeable devant celle de l'objet. Un tel pendule est appelé pendule pesant simple.
Le pendule pesant simple a une importance historique du fait que Galilée l'a étudié de façon détaillée et scientifique.
Étude théorique du modèle du pendule pesant simple
On peut établir l'équation différentielle du mouvement d'oscillation simplement à partir de la conservation de l'énergie mécanique. En négligeant les frottements, l'énergie mécanique du pendule est constante: elle est la somme de l'énergie cinétique et de l'énergie potentielle.
Dans le cas du modèle du pendule pesant simple, on considère que l'objet se ramène à une masse ponctuelle m, qui se déplace à la distance l de l'axe (longueur du fil ou de la tige, considérée inextensible et sans masse). On en déduit :
où :
- g est l'accélération de la pesanteur, et vaut en moyenne 9,81 m·s-2 en France.
- θ est l'angle que fait le pendule, à une date t, avec la verticale
- θ0 est l'angle maximal.
L'énergie mécanique étant constante dans le temps, sa dérivée est nulle. En dérivant la relation ci-dessus par rapport au temps on obtient après simplification :
Cette équation est celle d'un oscillateur non harmonique, c’est-à-dire non sinusoïdal.
La période T des oscillations dépend de l'amplitude du mouvement.
Par contre, la période ne dépend pas de la masse.
Expression exacte de la période des oscillations
En séparant les variables dans :
-
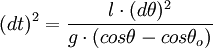 et en prenant la racine de cette dernière expression::
et en prenant la racine de cette dernière expression::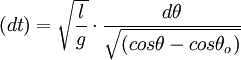
on obtient l'expression exacte de la période d'oscillations d'amplitude θo qui est :
Cette expression se déduit facilement en constatant que T= 4 fois le temps mis pour aller de 0 à θo
où K est une intégrale elliptique complète de première espèce qui vaut en première approximation ![]() et où
et où 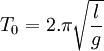 .
.
L'expression ![]() est connue sous le nom de formule de Borda.
est connue sous le nom de formule de Borda.
On peut également exprimer T sous forme de série. Si on pose 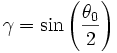 , alors :
, alors :
-
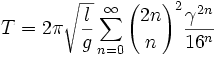 , où
, où 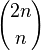 est un coefficient binomial.
est un coefficient binomial.
Si on développe γ en fonction de θ0, on obtient :
-
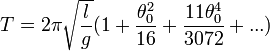 .
.
le tableau ci dessous donne les angles en degré, puis en radian dans les deux premières colonnes
ainsi que les valeurs de ![]() ,
, ![]() , et enfin
, et enfin ![]() :
:
| 10 | 0,175 | 1,00 | 1,00 | 1,00 |
| 20 | 0,349 | 1,01 | 1,01 | 1,01 |
| 30 | 0,524 | 1,02 | 1,02 | 1,02 |
| 40 | 0,698 | 1,03 | 1,03 | 1,03 |
| 50 | 0,873 | 1,05 | 1,05 | 1,05 |
| 60 | 1,047 | 1,07 | 1,07 | 1,07 |
| 70 | 1,222 | 1,09 | 1,10 | 1,10 |
| 80 | 1,396 | 1,12 | 1,14 | 1,14 |
| 90 | 1,571 | 1,15 | 1,18 | 1,18 |
| 100 | 1,745 | 1,19 | 1,22 | 1,23 |
| 110 | 1,920 | 1,23 | 1,28 | 1,30 |
| 120 | 2,094 | 1,27 | 1,34 | 1,37 |
| 130 | 2,269 | 1,32 | 1,42 | 1,47 |
| 140 | 2,443 | 1,37 | 1,50 | 1,60 |
| 150 | 2,618 | 1,43 | 1,60 | 1,76 |
| 160 | 2,793 | 1,49 | 1,71 | 2,01 |
| 170 | 2,967 | 1,55 | 1,83 | 2,44 |
| 180 | 3,142 | 1,62 | 1,96 |
On peut retenir que à un angle de θo de 50° la période est 5% plus grande que celle donnée par la formule simple :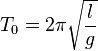 et que la correction due au second terme n'est perceptible qu'à des angles supérieurs à 70°
et que la correction due au second terme n'est perceptible qu'à des angles supérieurs à 70°
Expression approchée de la période de petites oscillations
Pour de faibles oscillations, l'équation différentielle peut approximativement s'écrire :
On voit donc que, pour de faibles amplitudes permettant d'approcher le sinus à son angle, le pendule se comporte comme un oscillateur harmonique. La période est alors indépendante de l'amplitude. On appelle ceci l'isochronisme des petites oscillations. Cette période s'exprime alors simplement par :
conformément à la limite de l'expression de Borda.
Période du pendule pesant composé
Pour un pendule pesant quelconque, l'effet de l'inertie sur la rotation ne peut pas être ramenée à une masse ponctuelle placée au centre de gravité. C'est l'ensemble du solide qui tourne, et son inertie est caractérisée par son moment d'inertie noté J et la distance l du centre de gravité à l'axe.
Aux faibles amplitudes, l'isochronisme des oscillations est aussi vérifié et la période correspondante s'exprime en fonction de J par :
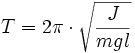 ; (pour le pendule simple J= M.l²)
; (pour le pendule simple J= M.l²)
Texte de Galilée concernant le pendule
(...) Quant aux temps d'oscillation de mobiles suspendus à des fils de différentes longueurs, ils ont entre eux même proportion que les racines carrées des temps ; si bien que pour obtenir un pendule dont le temps d'oscillation soit double de celui d'un autre pendule, il convient de donner au premier une longueur quadruple de celle du second ; de la même manière si un pendule a une longueur neuf fois supérieure à celle d'un autre pendule, celui-ci effectuera trois oscillations pendant que celui-là en accomplira une seule ; d'où il résulte que les longueurs des cordes sont inversement proportionnelles aux carrés du nombre des oscillations accomplies dans le même temps.
Sagredo : Si j'ai bien compris, je pourrai donc aisément connaître la longueur d'une corde attachée à une hauteur quelconque, quand bien même son point de suspension serait invisible et que l'on apercevrait seulement son extrémité inférieure. Si en effet j'attache en cette partie de la corde un poids fort lourd, auquel je communique un mouvement de va et vient, et si un ami compte le nombre de ces oscillations pendant que moi-même je compte les oscillations effectuées par un autre pendule suspendu à un fil mesurant exactement une coudée, alors grâce au nombre des oscillations de ces deux pendules durant un même temps, je trouverai la longueur de la corde ; supposons par exemple que mon ami ait compté vingt oscillations de la grande corde, dans le même temps où j'en comptais deux cent quarante pour mon fil long d'une coudée ; prenant les carrés des deux nombres vingt et deux cent quarante, c’est-à-dire 400 et 57 600, je dirai que la grande corde contient 57 600 des unités dont mon petit pendule contient 400, mais celui-ci mesure une seule coudée : je diviserai donc 57 600 par 400, ce qui donne 144, et je dirai que ma corde a une longueur de 144 coudées.
Salviati : Vous ne vous tromperiez même pas d'une palme surtout si vous prenez un grand nombre d'oscillations.
Sagredo : Vous me donnez à bien des reprises l'occasion d'admirer la richesse et aussi l'extrême libéralité de la nature, quand de choses si communes, et je dirais même d'une certaine façon triviales, vous faites surgir des connaissances aussi étonnantes que nouvelles, et souvent imprévues pour l'imagination. Il m'est bien arrivé mille fois de prêter attention à des oscillations, et notamment à celles de ces lampes d'église, suspendues à de longues cordes, et que quelqu'un par inadvertance avait mises en mouvement ; mais le plus que j'aie su tirer de telles observations est l'improbabilité de l'opinion selon laquelle semblables mouvements seraient entretenus par le milieu, c'est-à-dire par l'air, qui vraiment devrait avoir une grande sagacité, et en même temps peu de choses à faire, pour passer ainsi des heures et des heures à maintenir avec une telle régularité le balancement d'un poids. Quant à conclure que ce même mobile, suspendu à une corde de cent coudées, puis écarté de son point le plus bas tantôt de quatre vingt dix degrés, tantôt d'un degré ou d'un demi-degré seulement, ait besoin du même temps pour franchir le plus petit et le plus grand de ces arcs, cela, je crois, ne me serait jamais venu à l' esprit, et maintenant encore me semble tenir de l'impossible.
(...) En fin de compte j'ai pris deux boules, l'une en plomb et l'autre en liège, celle-là au moins cent fois plus lourde que celle-ci, puis j'ai attaché chacune d'elles à deux fils très fins, longs tous deux de quatre ou cinq coudées ; les écartant alors de la position perpendiculaire, je les lâchai en même temps et celle-ci, suivant les circonférences des cercles ayant les fils égaux pour rayons, dépassaient la perpendiculaire pour remonter de l'autre côté, par la même voie ; une bonne centaine d'allées et venues, accomplies par les boules elles-mêmes, m'ont clairement montré qu'entre la période du corps pesant et celle du corps léger, la coïncidence est telle que sur mille vibrations comme sur cent, le premier n'acquiert sur le second aucune avance, fût-ce la plus minime, mais que tous deux ont un rythme de mouvement rigoureusement identique. On observe également l'action du milieu qui, en gênant le mouvement, ralentit bien davantage les vibrations du liège que celles du plomb, sans toutefois modifier leur fréquence ; même si les arcs décrits par le liège n'ont plus que cinq ou six degrés, contre cinquante ou soixante pour le plomb, ils sont en effet traversés en des temps égaux.
Commentaire sur le texte :
en italiques sont indiquées les lois du pendule selon Galilée. Notez qu'il s'est trompé sur la deuxième n'ayant pas la précision voulue dans ses mesures pour observer la dépendance de la période en fonction de l'amplitude.
Applications
La première définition de la seconde fut la demi-période d'un pendule de un mètre de long. (La seconde n'est plus définie mécaniquement, mais par un nombre bien défini de périodes d'une transition dans un atome de Césium).
Soit L0 la longueur d'un pendule ayant une période de T0 = 2 secondes :
- un pendule de L0/4 aura une période de 1s
- un pendule de longueur L aura une période telle que:
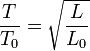
En élevant au carré le rapport des périodes, on obtient le rapport des longueurs des pendules.
Les horloges franc-comtoises, ou pendules (nom féminin), utilisent un balancier qui est un pendule pesant. On règle la période d'oscillation en faisant bouger une masse le long du balancier.