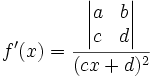Fonction homographique - Définition
On appelle fonction homographique toute fonction d'un corps commutatif ![]() dans lui-même définie par
dans lui-même définie par
où a, b, c et d sont des éléments de ![]() , c étant non nul et (a , b) étant non proportionnel à (c , d)
, c étant non nul et (a , b) étant non proportionnel à (c , d)
Cette fonction détermine une bijection de ![]() dans
dans ![]() .
.
Sa réciproque est
Le nom provient de ce que si on rajoute à ![]() un point à l'infini
un point à l'infini ![]() de sorte à en faire une droite projective, et si l'on prolonge
de sorte à en faire une droite projective, et si l'on prolonge ![]() par
par ![]() , et
, et ![]() , on obtient une homographie de
, on obtient une homographie de ![]() . Et les homographies (plus celles du plan que celles de la droite il est vrai) transforment un graphique en un graphique ayant des homologies avec celui de départ...
. Et les homographies (plus celles du plan que celles de la droite il est vrai) transforment un graphique en un graphique ayant des homologies avec celui de départ...
Dans le cas réel ou complexe, Sa dérivée est
où 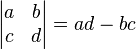 est le déterminant de
est le déterminant de ![]()
Sa représentation graphique dans le cas réel est une hyperbole qui se déduit de l'hyperbole d'équation y = 1/x par une translation et une affinité.
Dans le plan complexe
A chaque fonction homographique complexe, on peut associer une fonction ponctuelle F qui, au point M d'affixe z, associe le point M' d'affixe f(z).
On peut distinguer les cas suivants
- si c = 0 alors F est une similitude directe
- si c est non nul, on peut prouver que F est la composée d'une inversion et de similitudes
La fonction F conserve le birapport de 4 points distincts non alignés.
Propriété géométriques des coniques
Une fonction homographique peut servir à tracer une conique. Pour cela il suffit de prendre deux tangentes à cette conique, sur la première tangente prendre un point X de coordonnée x, de faire une transformation homographique y=f(x) avec les paramètres (a, b c et d) judicieusement choisis de placer sur la deuxième tangente le point Y de coordonnée y. La droite (XY) sera tangente à la conique, mais on ignore la position du point de contact sur cette droite. Exemple: Construction d'une parabole tangente par tangente. De même on peut tracer une conique point à point en faisant subir une fonction homographique aux coordonnées de deux faisceaux de droites. Exemple: Construction d'un cercle point par point.
Propriétés algébriques
Les fonctions homographiques se composent comme des matrices : si ![]() alors
alors ![]() où
où ![]() .
.
Plus précisément on a ainsi une représentation du groupe ![]() dans celui des fonctions homographiques (à un problème de définition près au point
dans celui des fonctions homographiques (à un problème de définition près au point ![]() ), dont le noyau est le centre de
), dont le noyau est le centre de ![]() .
.
Voir plus généralement la page sur les homographies.