Distance de Hamming - Définition
La distance de Hamming, définie par Richard Hamming, est utilisée en informatique, en traitement du signal et dans les télécommunications. Elle joue un rôle important en théorie algébrique des codes correcteurs. Elle permet de quantifier la différence entre deux séquences de symboles.
La distance de Hamming est une distance au sens mathématique du terme. À deux suites de symboles de même longueur, elle associe l'entier désignant le cardinal de l'ensemble des symboles de la première suite qui différent de la deuxième.
Le poids de Hamming correspond au nombre d'éléments différents de zéro dans une chaine d'éléments d'un corps fini.
Intérêt du concept
Histoire et domaine d'applications
La distance de Hamming doit son nom à Richard Hamming (1915 1998). Elle est décrite dans un article[1] fondateur pour la théorie des codes. Elle est utilisée en télécommunication pour compter le nombre de bits altérés dans la transmission d'un message d'une longueur donnée. Le poids de Hamming correspond au nombre de bits différents de zéro, il est utilisé dans plusieurs disciplines comme la théorie de l'information, la théorie des codes et la cryptographie. Néanmoins, pour comparer des séquences de longueurs variables, ou des chaines de caractères pouvant subir non seulement des substitutions, mais aussi des insertions ou des effacements, des métriques plus sophistiquées comme la distance de Levenshtein sont plus adaptées.
Motivation
Les codes correcteurs ont leur source dans un problème de la transmission de données. Parfois, une transmission de données se fait en utilisant une voie de communication non entièrement fiable. L'objectif d'un code correcteur est l'apport d'une redondance de l'information de telle manière à ce que l'erreur puisse être détectée voir corrigée.
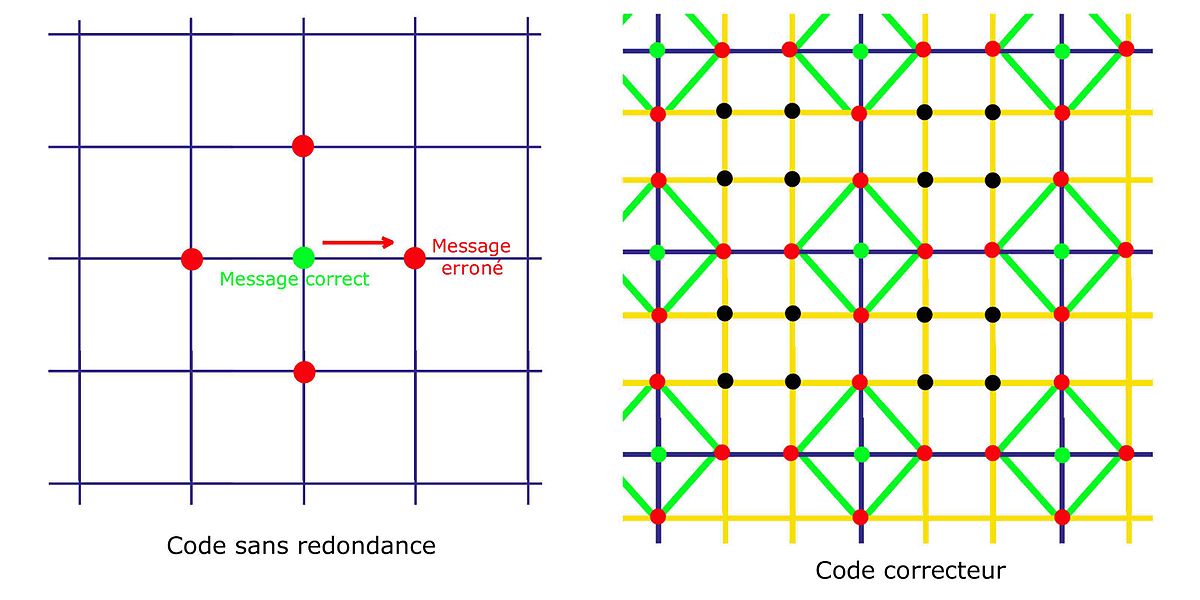
Un message est un élément d'un ensemble E constitué de suites finies de lettres choisies dans un alphabet A. L'apport de la redondance est le résultat d'une application injective φ de E dans un ensemble F constitué aussi de suite finies de lettres d'un alphabet A'. Les suites de l'ensemble F sont choisies a priori plus longues que celle de E. L'ensemble φ(E) est appelé code et un élément de cet ensemble φ(m) mot du code. L'intérêt de transmettre φ(m) à la place de m est illustré par la figure à droite :
Le cas d'un code sans redondance est illustré à gauche sur la figure. F est alors égal à E et φ est l'identité. Si un message en vert subit, lors de sa transmission, une altération, un nouveau message en rouge est transmis. Aucune information ne laisse supposer qu'une erreur a été commise.
Pour pallier cet état, l'objectif est d'entourer les mots du code, correspondant, sur la figure de droite aux points verts, par des messages connus pour contenir des erreurs. Ces redondances sont illustrées par les intersections du quadrillage orange. Si une unique erreur se produit, alors le message transmis correspond à un point rouge. Si la redondance a été habilement construite, il n'existe qu'un point vert proche du point rouge reçu, l'erreur est corrigible.
La distance de Hamming correspond sur la figure au plus petit nombre de segments du quadrillage à traverser pour joindre deux points.
Définition et exemples
Définitions
- Soit A un alphabet et F l'ensemble des suites de longueur n à valeur dans A. La distance de Hamming entre deux éléments a et b de F est le cardinal de l'ensemble des images de a qui diffèrent de celle de b.
Formellement, si d(.,.) désigne la distance de Hamming :
![\forall a,b \in F \quad a = (a_i)_{i\in [0, n-1]} \; et \; b = (b_i)_{i\in [0, n-1]} \quad d(a,b) = \#\{ i : a_i\neq b_i \}](https://static.techno-science.net/illustration/Definitions/autres/7/71699525f9403e3b1588348a97f277d7_a10d9819dd394a9a9bd35c66f9487ed7.png){kind=small}
La notation #E désigne le cardinal de l'ensemble E.
Un cas important dans la pratique est celui des symboles binaires. Autrement dit A= {0,1}, On peut alors écrire, si ⊕ désigne le ou exclusif.
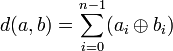
Dans le cas, fréquent, où l'alphabet est un corps fini, F possède une structure d'espace vectoriel de dimension n. La distance dérive alors d'une pseudo-norme :
- Soit K est un corps fini et F l'ensemble des suites de longueur n à valeur dans K. Le poids de Hamming p(a) d'un élément a de F est le cardinal de l'ensemble des images de a non nulles.
L'alphabet est souvent F2 le corps à deux éléments {0,1}. Le poids de Hamming est une pseudo-norme car :
Néanmoins, si l'alphabet est un corps fini, alors la distance dérive du poids de Hamming, en effet:
Exemples
Considérons les suites binaires suivantes :
La distance entre a et b est égale à 3 car 3 bits diffèrent.
- La distance de Hamming entre 1011101 et 1001001 est 2.
- La distance de Hamming entre 2143896 et 2233796 est 3.
- La distance de Hamming entre "ramer" et "cases" est 3.
Cas binaire
Un cas important est celui ou l'alphabet est le corps à deux éléments {0,1}. Une lettre est alors appelée bit. Il est largement utilisé en informatique et en télécommunication.
Il est possible d'illustrer graphiquement le code et les distances entre les différents mot.
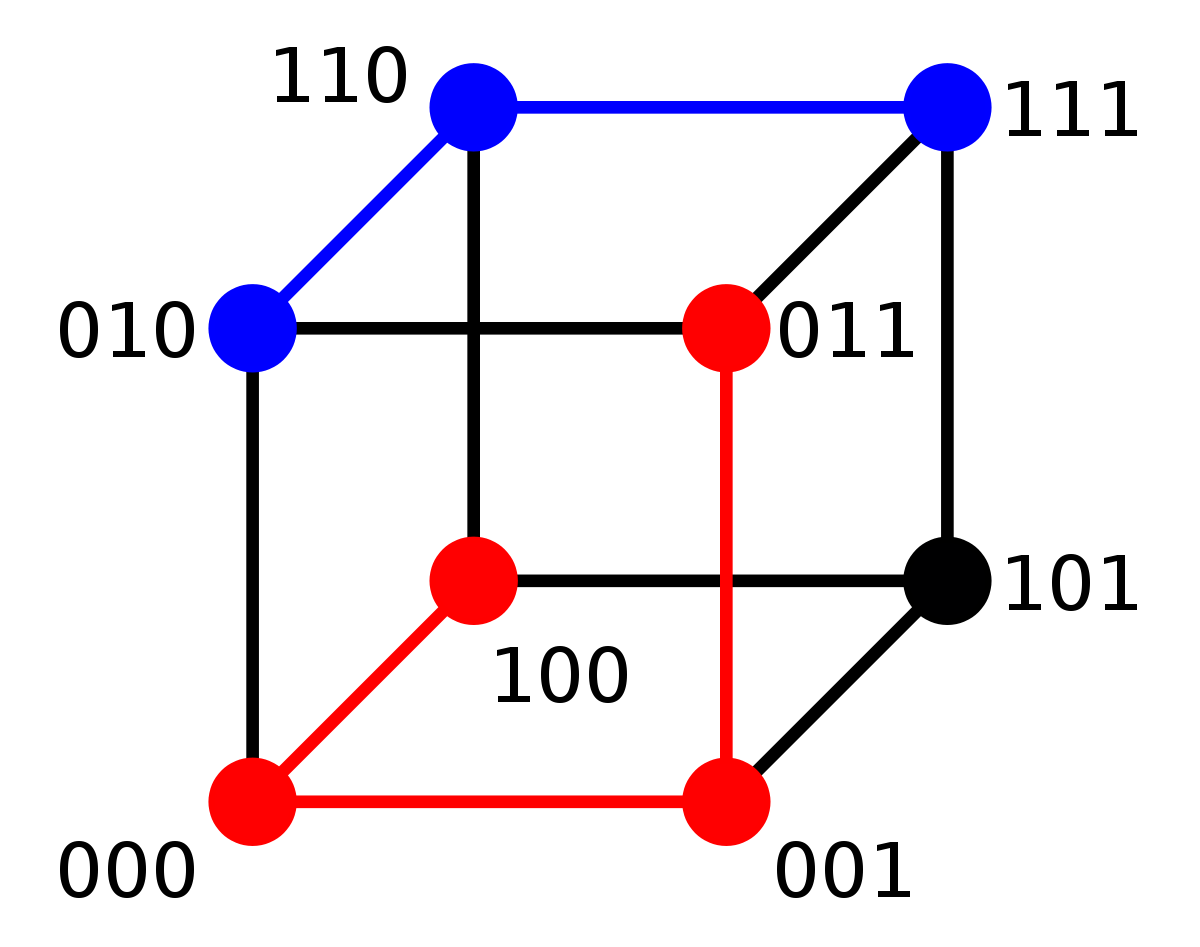
Le cas ou un mot comporte trois lettres est illustré sur la figure de gauche. La distance entre 010 et 111 est égale à deux car il est nécessaire de parcourir deux segments pour joindre les deux points. La distance pour joindre les points 100 et 011 est égale à trois.
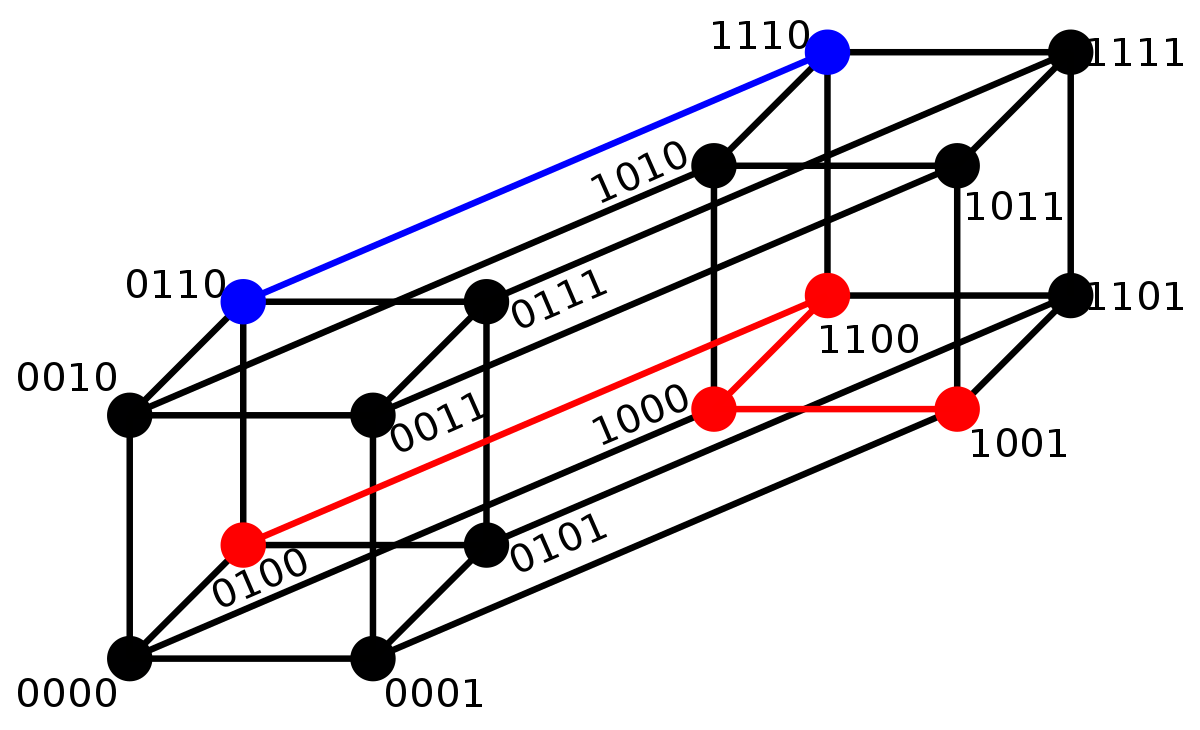
La figure de droite illustre un hyper-cube binaire de dimension quatre. La distance entre 0110 et 1110 est égale à un, alors que la distance entre 0100 et 1001 est égal à trois.
Le poids de Hamming d'un élément a correspond à la distance entre le mot zéro n'ayant que des coordonnées nulles et a.
Propriété
Distance
La distance de Hamming est une distance au sens mathématique du terme :
 |
(symétrie) |
 |
(séparation) |
 |
(inégalité triangulaire) |
La troisième propriété se démontre par une récurrence sur n.
Capacité de correction et distance minimale
La distance minimale δ est le minimum de distance entre deux mots du codes. Elle permet de déterminer le nombre maximal d'erreurs t corrigeables de manière certaine. La valeur de t est en effet celle du plus grand entier strictement inférieur à δ/2.
Si M désigne le nombre de mot du code, q le nombre de lettres de l'alphabet A de F et Vt le cardinal d'une boule fermée de rayon t, alors la majoration suivante est vérifiée:
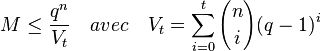
Cette majoration porte le nom de Borne de Hamming.
Dans le cas d'un code linéaire, et si k désigne la longueur des mots du codes, il existe une autre majoration, dite du borne du singleton :
Applications
Somme de contrôle
| Données sur 7 bits | avec bit de parité |
|---|---|
| 0000000 | 00000000 |
| 1010001 | 11010001 |
| 1101001 | 01101001 |
| 1111111 | 11111111 |
La somme de contrôle est un exemple simple d'utilisation de la distance de Hamming. La distance minimale entre deux mots du code est égale à deux. En conséquence, si une unique erreur se produit elle est détectée. En revanche, elle n'est pas corrigeable sans retransmission. En effet, il existe a priori plusieurs mots de code à distance de un du message erroné.
L'exemple le plus simple est celui du bit de parité. Il correspond à une somme de contrôle dans le cas où le corps est binaire, c'est-à-dire qu'il contient deux éléments zéro et un.
Supposons que l'objectif soit la transmission de sept bits. Un bit de parité est défini comme étant égal à zéro si la somme des autres bits est paire et à un dans le cas contraire. Les huit bits transmis sont d'abord le bit de parité puis les sept bits du message. Il correspond au bit de parité pair, c'est-à-dire la deuxième colonne du tableau de droite. Les messages envoyés sur huit bits ont toujours la parité zéro, ainsi si une erreur se produit, un zéro devient un un, ou l'inverse; le recepteur sait qu'une altération a eu lieu. En effet la somme des bits devient impaire ce qui n'est pas possible sans erreur de transmission.
Code de Hamming
Le code de Hamming est un exemple un peu plus complexe que le précédent. La distance minimale entre deux mots du code est égale à trois. Si une unique altération se produit, alors le message reçu est à une distance de un d'un unique point du code. Il est ainsi possible de corriger automatiquement une erreur, si l'on sait que l'erreur est unique.
Code linéaire
Les codes linéaires forment une famille contenant les deux exemples précédents. L'alphabet est un corps fini, les ensembles E et F sont des espaces vectoriels et l'application φ est linéaire. La distance de Hamming dérive de la pseudo-norme : le poids de Hamming. Ce contexte est très généralement celui qu'utilise l'industrie.
Code cyclique
Cette famille de codes correspond à un cas particulier de code linéaire. Les structures E et F sont enrichies d'une structure d'anneau leur conférant le statut d'algèbre. Cette structure, se fondant sur la théorie polynômes sur les extensions de corps finis permet de construire des distances minimales aussi élevées qu'on le souhaite.
De nombreux codes sont construits sur cette théorie. Le code de Hamming apparait comme un cas particulier de ceux là. On peut citer aussi les codes BCH ou les codes de Reed-Solomon utilisés par exemple pour les disques compacts.
Notes et références
| Articles de Théorie des codes en rapport avec les codes correcteurs |
| Code correcteur | Code de répétition | Somme de contrôle | Distance de Hamming | Code parfait et code MDS | Code de Hamming | Code de Hamming (7,4) | Code linéaire | Matrice génératrice | Matrice de contrôle | Décodage par syndrome | Identité de Mac Williams | Code cyclique |