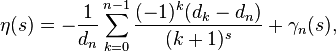Fonction eta de Dirichlet - Définition

La fonction eta de Dirichlet peut être définie par

où est la fonction zeta de Riemann. Néanmoins, elle peut aussi être utilisée pour définir la fonction zeta. Elle possède une expression en série de Dirichlet, valide pour tout nombre complexe s avec une partie réelle positive, donnée par

.

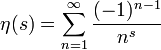Tandis que ceci est convergent seulement pour s avec une partie réelle positive, elle est sommable au sens d'Abel pour tout nombre complexe, qui servent à définir la fonction eta comme une fonction entière, et montre que la fonction zeta est méromorphe avec un pôle singulier en s = 1.

De manière équivalente, nous pouvons commencer par définir

qui est aussi définie dans la région de la partie réelle positive. Ceci présente la fonction eta comme une transformation de Mellin.

Hardy a donné une démonstration simple de l'équation fonctionnelle pour la fonction eta, qui est

.

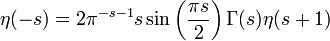A partir de cela, on a immédiatement l'équation fonctionnelle de la fonction zeta également, cela nécessite d'étendre la définition de la fonction eta au plan complexe entier.

Méthode de Borwein

Peter Borwein a utilisé des approximations impliquant les polynômes de Tchebychev pour concevoir une méthode pour une évaluation efficace de la fonction eta. Si 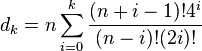alors

où le terme erroné est borné par

où .

Publications

Borwein, P., An Efficient Algorithm for the Riemann Zeta Function, Constructive experimental and nonlinear analysis, CMS Conference Proc. 27 (2000), 29-34 ou http://www.cecm.sfu.ca/~pborwein/