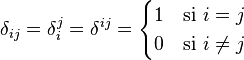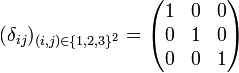Symbole de Kronecker - Définition
En mathématiques, le symbole de Kronecker est une fonction de deux variables qui est égale à 1 si celles-ci sont égales, et 0 sinon. Il est symbolisé par la lettre δ (delta minuscule) de l'alphabet grec, et est considéré comme une convention d'écriture plutôt que comme une fonction.
Ou, en notation tensorielle :
où δi et δj sont des vecteurs unitaires tels que seule la i-ème (respectivement la j-ème) coordonnée soit non nulle (et vaille donc 1).
Ce symbole a été nommé en l'honneur du mathématicien Léopold Kronecker (1823 - 1891).
Il est utilisé dans de nombreux domaines mathématiques. Par exemple en algèbre linéaire, la matrice identité d'ordre 3 peut s'écrire :
Symbole de Kronecker et sommations
Lors de sommation, le symbole de Kronecker provoque de spectaculaires simplifications :