Dodécaèdre - Définition
 |
|
| Type | Polyèdre régulier |
|---|---|
| Faces | Pentagone |
| Éléments : · Faces · Arêtes · Sommets · Caractéristique |
12 30 20 2 |
| Faces par sommet | 3 |
| Sommets par face | 5 |
| Isométries | Ih |
| Dual | Icosaèdre |
| Propriétés | Deltaèdre régulier et convexe |
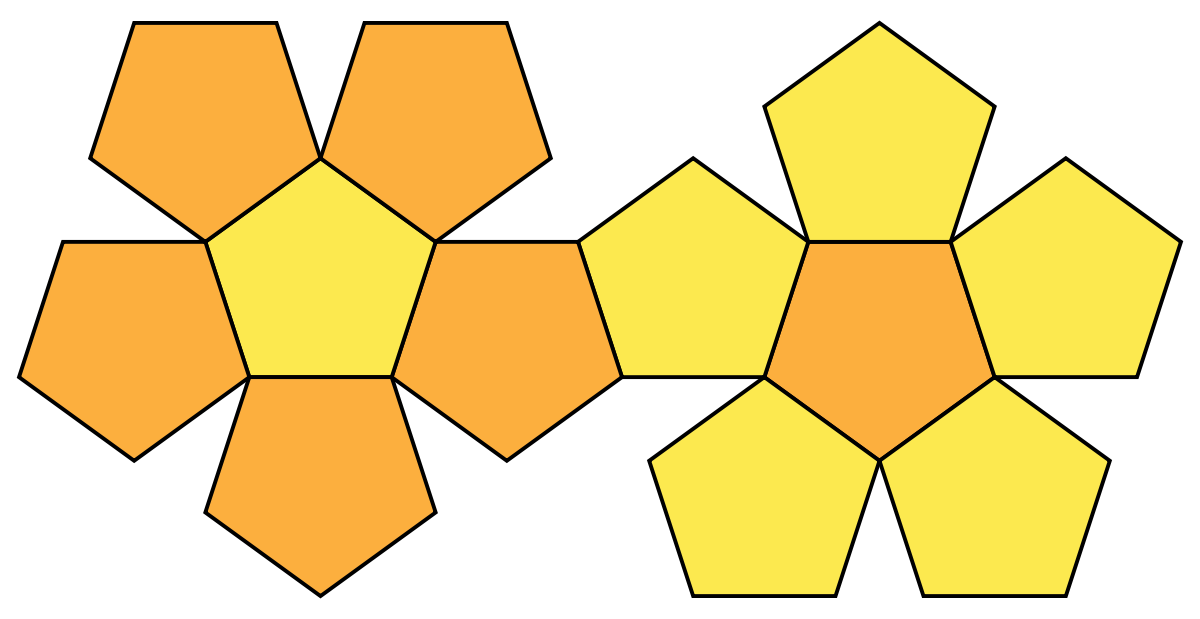
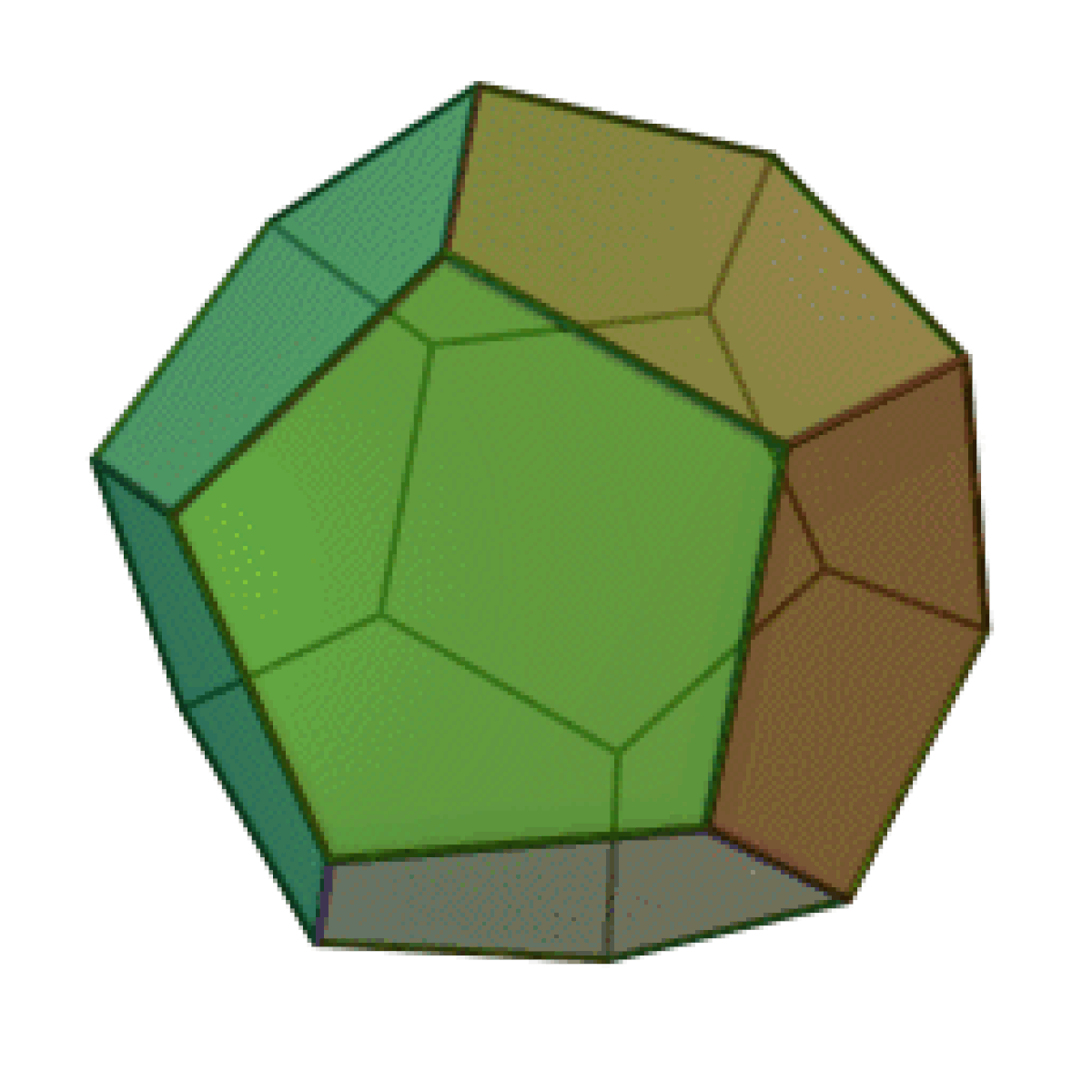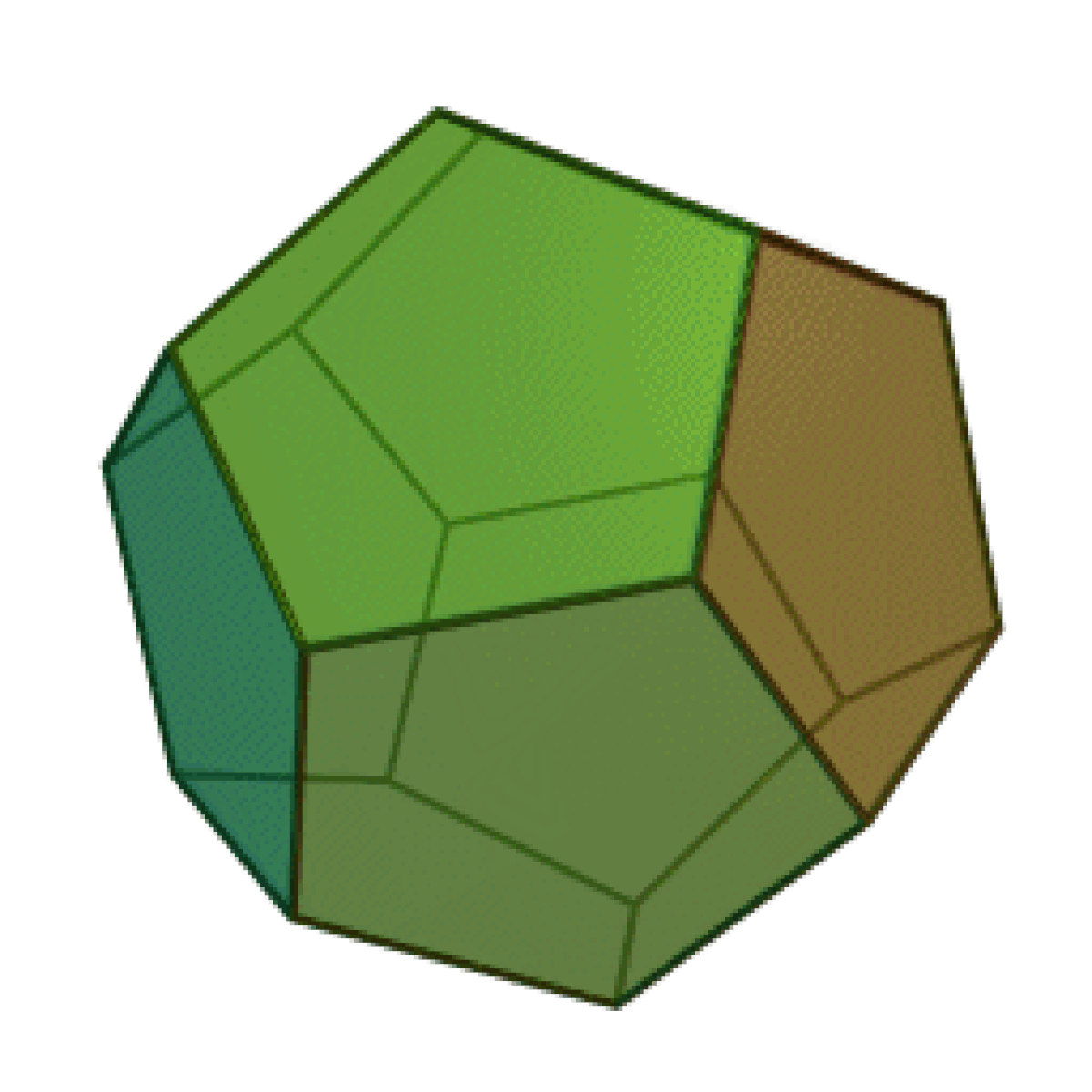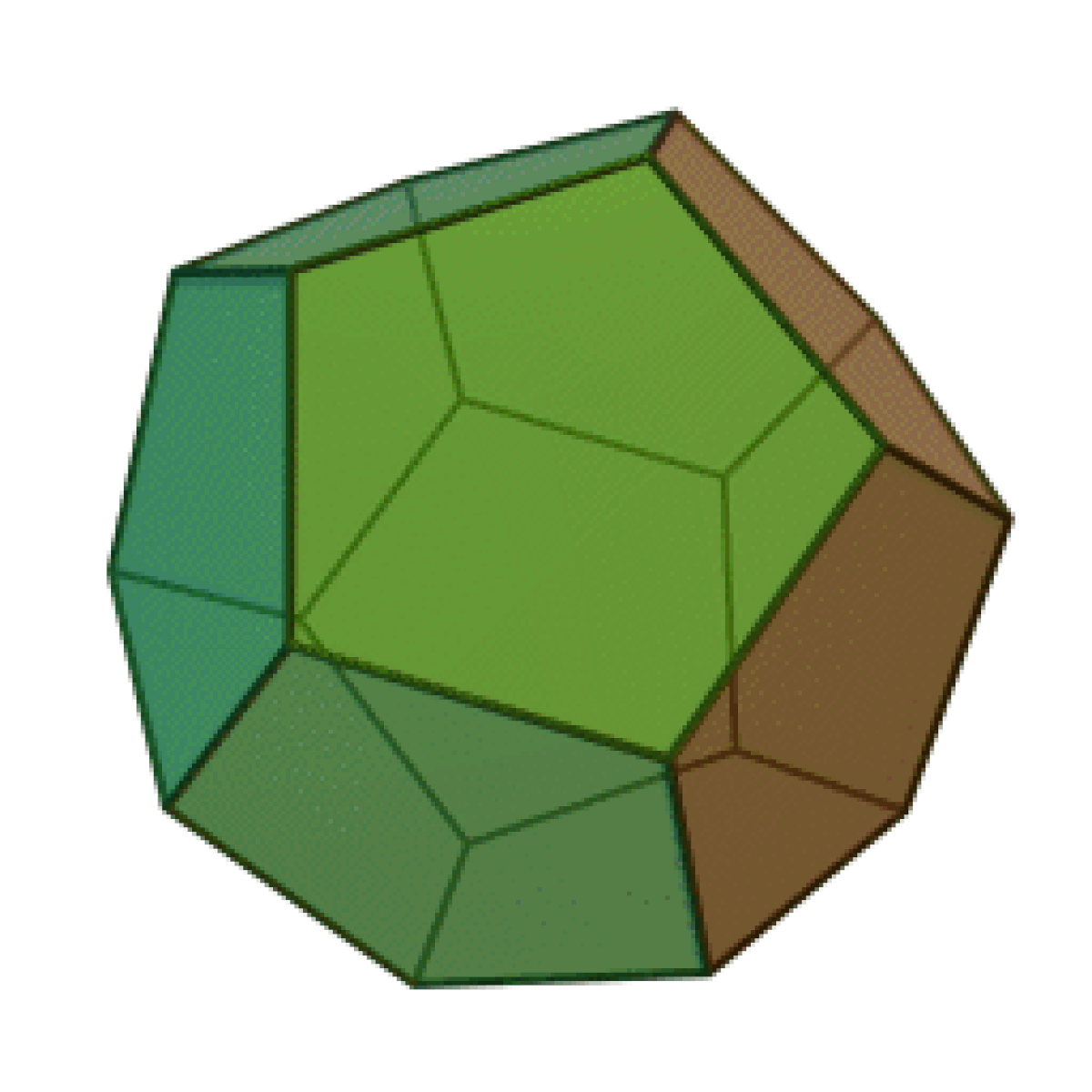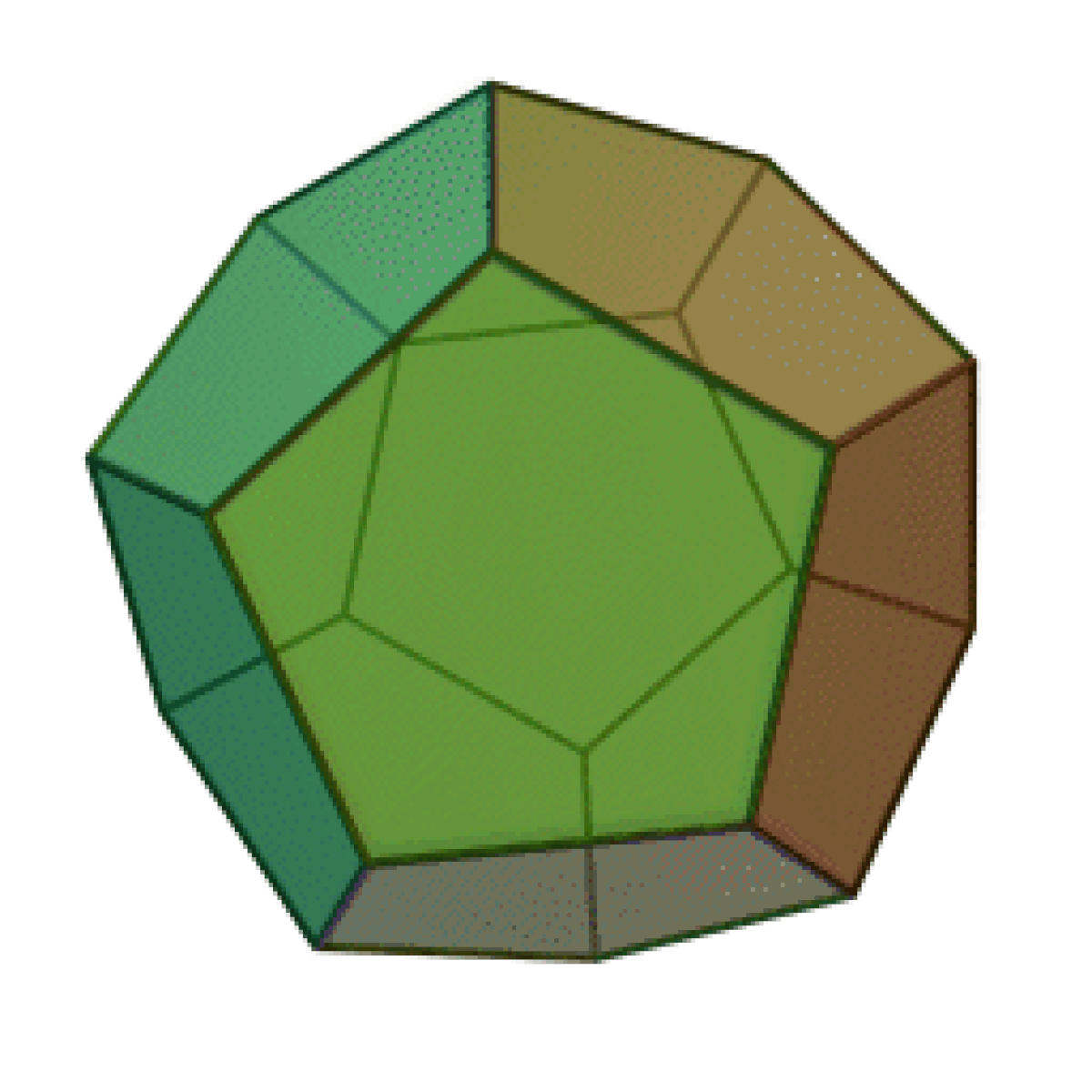
Un dodécaèdre est un solide composé de 12 faces. Le préfixe dodéca-, d'origine grecque, fait référence au nombre de faces.
Dodécaèdre régulier
Un dodécaèdre régulier est un solide de Platon composé de faces pentagonales, dont 3 se rejoignent à chaque sommet.
Les coordonnées canoniques pour un dodécaèdre centré sur l'origine :
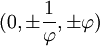 ,
,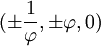 ,
,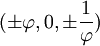 ,
,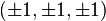 ,
,
où ![]() est le nombre d'or.
est le nombre d'or.
Si a est la longueur d'une arête :
- La surface est égale à :
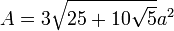
et le volume à :
L'angle dièdre entre deux faces vaut :
soit environ 116°5650512.
| Les solides géométriques | ||||
| Les solides de Platon | ||||
| Tétraèdre - Cube - Octaèdre - Icosaèdre - Dodécaèdre | ||||
| Les solides d'Archimède | ||||
| Tétraèdre tronqué - Cube tronqué - Octaèdre tronqué - Dodécaèdre tronqué - Icosaèdre tronqué - Cuboctaèdre - Cube adouci - Icosidodécaèdre - Dodécaèdre adouci - Petit rhombicuboctaèdre - Grand rhombicuboctaèdre - Petit rhombicosidodécaèdre - Grand rhombicosidodécaèdre | ||||
| Les solides de Kepler-Poinsot | ||||
| Petit dodécaèdre étoilé - Grand dodécaèdre étoilé - Grand dodécaèdre - Grand icosaèdre | ||||
| Les solides de Catalan | ||||
| Triakioctaèdre - Tétrakihexaèdre - Triakitétraèdre - Pentakidodécaèdre - Triaki-icosaèdre - Dodécaèdre rhombique - Icositétraèdre pentagonal - Triacontaèdre rhombique - Hexacontaèdre pentagonal - Icositétraèdre trapézoïdal - Hexakioctaèdre - Hexacontaèdre trapézoïdal - Hexaki icosaèdre | ||||
| Les solides de Johnson | ||||
| Les solides de révolution | ||||
| Sphère - Cylindre de révolution - Cône de révolution - Tore - Paraboloïde de révolution |
Populaires