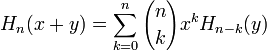Polynôme d'Hermite - Définition
En mathématiques, les polynômes d'Hermite sont une suite de polynômes qui ont été nommés ainsi en l'honneur de Charles Hermite. Ils sont définis comme suit :
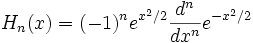(forme dite probabiliste)
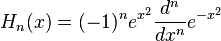(forme dite physique)
Les deux définitions ne sont pas tout à fait équivalentes ; les polynômes d'une définition sont en " compression " ou en " expansion " par rapport à l'autre définition.
On peut effectuer le passage d'une forme à l'autre grâce à la relation suivante: 
.
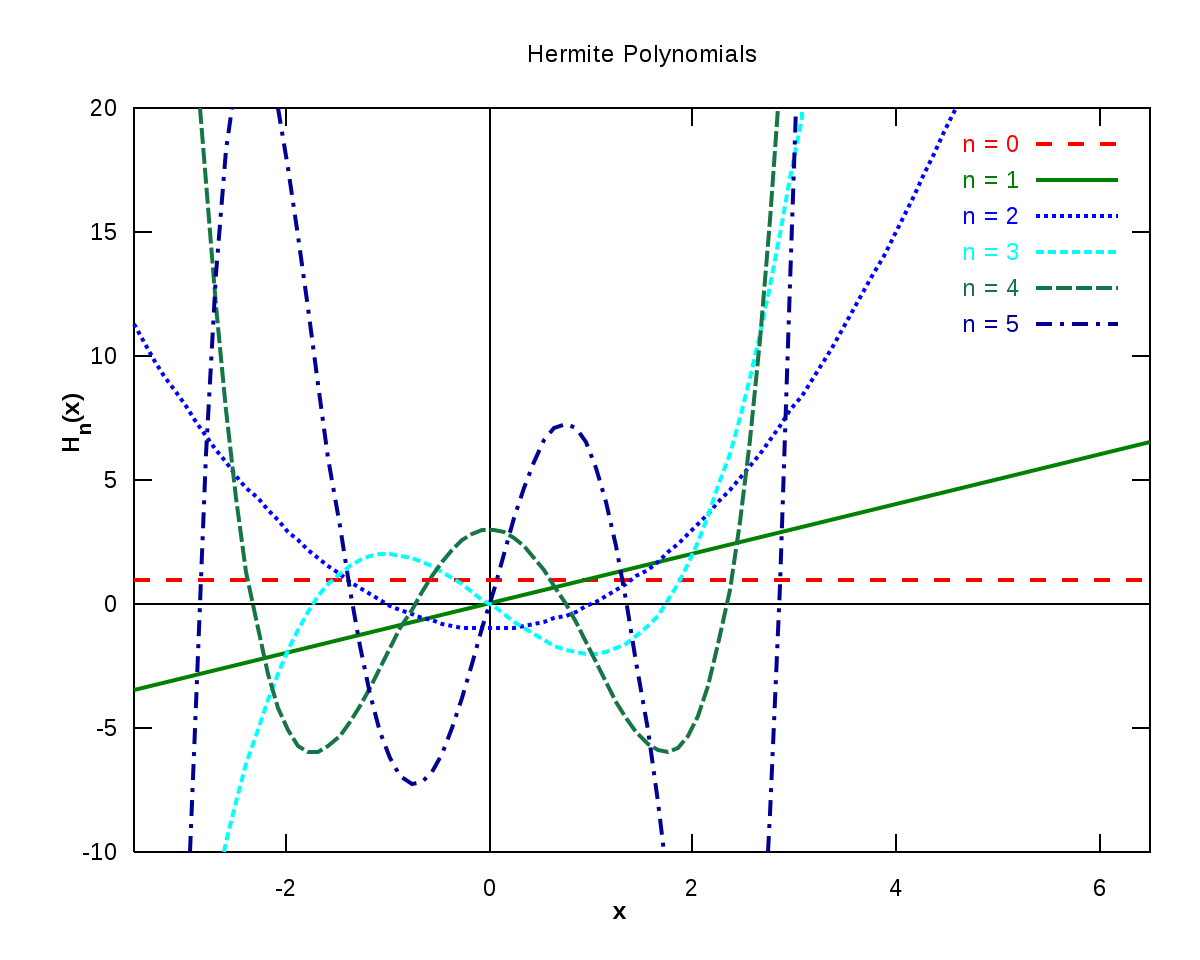
Les premiers polynômes d'Hermite sont les suivants (forme "probabiliste") :
on peut en réalité démontrer que le coefficient 
de 
vaut -p(p-1)/4 et que bien sûr le coefficient 
de est toujours nul.
Sous leur forme "physique", les premiers polynômes sont:
Orthogonalité
La n-ième fonction de la suite est un polynôme de degré n. Ces polynômes sont orthogonaux pour la mesure
c'est-à-dire que :
où δn m est le symbole de Kronecker, qui vaut 1 quand n = m et 0 sinon. Ces fonctions forment une base orthogonale d'un espace de Hilbert où les fonctions satisfont la propriété suivante :
dans laquelle le produit scalaire est donné par l'intégrale
Diverses propriétés
Le n-ième polynôme d'Hermite satisfait l'équation différentielle suivante :
On a aussi la suite récurrente suivante :
Les polynômes satisfont la propriété
que l'on peut écrire ainsi
