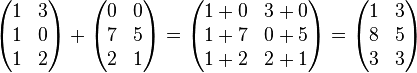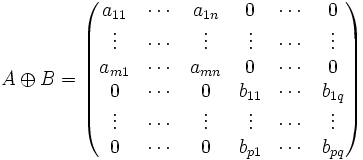Addition matricielle - Définition
L'addition des matrices est définie pour deux matrices de même type. La somme de deux matrices de type (m, n), A = (aij) et B = (bij), notée A + B, est à nouveau une matrice (cij) de type (m, n) obtenue en additionnant les éléments correspondants, i.e.,
- pour tous i, j,
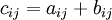
Par exemple:
L'ensemble des matrices de type (m, n) avec la loi d'addition forment un groupe abélien.
Cette notion d'addition des matrices provient de celle des applications linéaires; si A et B sont interprétées comme des matrices d'applications linéaires relativement à des bases données, alors la matrice somme A+B représente la matrice de la somme des deux applications linéaires par rapport à ces mêmes bases.
Pour toutes matrices quelconques A (de taille m × n) et B (de taille p × q), il existe la somme directe de A et B, notée ![]() et définie par :
et définie par :
Par exemple :
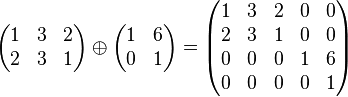
| Articles de mathématiques en rapport avec l'algèbre linéaire |
| Espace vectoriel | Base | Dimension | Matrice | Application linéaire | Déterminant | Trace | Rang | Théorème des facteurs invariants | Réduction d'endomorphisme | Réduction de Jordan | Décomposition de Dunford | Valeur propre | Polynôme caractéristique | Forme linéaire | Espace dual | Orthogonalité | Produit scalaire | Produit vectoriel | Polynôme d'endomorphisme | Polynôme minimal | Tenseur | Pseudovecteur | Covecteur | Algèbre multilinéaire |