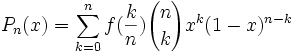Continuité uniforme - Définition
En topologie, la continuité uniforme est une définition plus contraignante que la continuité, et se définit dans les espaces métriques ou les espaces uniformes. Contrairement à la continuité, la continuité uniforme n'est pas une notion " purement topologique " c'est-à-dire ne faisant intervenir que des ouverts : sa définition dépend de la distance ou de la structure uniforme.
Continuité uniforme dans un espace métrique
Définition
Soient ![]() et
et ![]() deux espaces métriques, et
deux espaces métriques, et ![]() une application de
une application de ![]() vers
vers ![]() .
.
On dira que ![]() est uniformément continue si et seulement si :
est uniformément continue si et seulement si :
NB: La continuité " simple " de ![]() s'écrit par comparaison :
s'écrit par comparaison :
On comprend alors le sens du mot " uniforme " : le choix de ![]() en fonction de
en fonction de ![]() ne dépend pas du point considéré, il est uniforme sur
ne dépend pas du point considéré, il est uniforme sur ![]() .
.
- Cas des fonctions d'une variable réelle et à valeurs réelles
Dans le cas où l'espace de départ ![]() et l'espace d'arrivée
et l'espace d'arrivée ![]() sont des intervalles de
sont des intervalles de ![]() munis de la norme valeur absolue, la définition s'écrit :
munis de la norme valeur absolue, la définition s'écrit :
Exemples
Exemple 1 : ![]()
![]() est uniformément continue ; en effet :
est uniformément continue ; en effet :
Soit ![]() 0 \,\!" />. Comme la fonction
0 \,\!" />. Comme la fonction ![]() est concave on a pour tous
est concave on a pour tous ![]() :
:
![]() .
.
Posons alors ![]() ; si
; si ![]() vérifient
vérifient ![]() alors :
alors :
![]() , ce qu'il fallait démontrer.
, ce qu'il fallait démontrer.
Exemple 2 : ![]()
![]() n'est pas uniformément continue ; en effet, montrons que :
n'est pas uniformément continue ; en effet, montrons que :
![]() 0,\ \forall \eta > 0,\ \exists (x,y) \in \R_+ \times \R_+ \ , |x-y| \leq \eta \ et \ |f_2(x)-f_2(y)|>\varepsilon \,\!" />.
0,\ \forall \eta > 0,\ \exists (x,y) \in \R_+ \times \R_+ \ , |x-y| \leq \eta \ et \ |f_2(x)-f_2(y)|>\varepsilon \,\!" />.
En fait ![]() convient. Pour n'importe quel
convient. Pour n'importe quel ![]() 0 \,\!" /> on choisit
0 \,\!" /> on choisit ![]() et
et ![]() . Alors
. Alors ![]() et
et ![]() \varepsilon \,\!" />, ce qu'il fallait démontrer.
\varepsilon \,\!" />, ce qu'il fallait démontrer.
Résultats importants
Fonctions lipschitziennes
Soit ![]() un intervalle quelconque de
un intervalle quelconque de ![]() . Toute fonction lipschitzienne
. Toute fonction lipschitzienne ![]() est uniformément continue.
est uniformément continue.
En particulier, si ![]() est dérivable et de dérivée bornée sur
est dérivable et de dérivée bornée sur ![]() , alors
, alors ![]() est uniformément continue.
est uniformément continue.
Théorème de Heine
Soient ![]() et
et ![]() deux espaces métriques, et une application continue
deux espaces métriques, et une application continue ![]() .
.
Si ![]() est compact, alors
est compact, alors ![]() est uniformément continue.
est uniformément continue.
En particulier, toute fonction ![]() continue sur le segment
continue sur le segment ![]() de
de ![]() est uniformément continue.
est uniformément continue.
Prolongement par continuité
Toute fonction uniformément continue à valeurs réelles se prolonge par continuité sur l' adhérence de son espace de départ. Cette propriété est utilisée parfois pour définir des fonctions importantes comme l'intégrale ou l'exponentielle.
Intérêt de la notion d'uniforme continuité
Approximation uniforme des fonctions continues par les fonctions en escalier
Soit f une fonction continue sur un segment [a,b] et soit ![]() 0" />. Alors il existe une fonction en escalier
0" />. Alors il existe une fonction en escalier ![]() sur [a,b], telle que :
sur [a,b], telle que :
On utilise pour cela le fait que f est en fait uniformément continue (théorème de Heine), et on découpe l'intervalle [a,b] en n sous-intervalles de longueur ![]() inférieure au η intervenant dans la définition de l'uniforme continuité. On montre alors que la fonction
inférieure au η intervenant dans la définition de l'uniforme continuité. On montre alors que la fonction ![]() valant f(a + k(b − a) / n) sur l'intervalle [a + k(b − a) / n,a + (k + 1)(b − a) / n] convient.
valant f(a + k(b − a) / n) sur l'intervalle [a + k(b − a) / n,a + (k + 1)(b − a) / n] convient.
Définition de l'intégrale de Riemann
Soit E l'espace vectoriel des fonctions bornées sur l'intervalle [a,b], muni de la norme de la convergence uniforme. Soit F le sous-espace des fonctions en escalier sur [a,b]. Il est aisé de définir l'intégrale ![]() d'une telle fonction en escalier
d'une telle fonction en escalier ![]() , au moyen d'une somme finie
, au moyen d'une somme finie 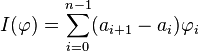 si
si ![]() est constante égale à
est constante égale à ![]() sur l'intervalle ]ai,ai + 1[, les ai constituant une subdivision de [a,b]. On montre alors que I est une fonction lipschitzienne sur F, donc uniformément continue, donc se prolonge à l'adhérence de F dans E. Cette adhérence constitue l'espace des fonctions réglées, et contient les fonctions continues. On a défini ainsi l'intégrale de Riemann des fonctions réglées.
sur l'intervalle ]ai,ai + 1[, les ai constituant une subdivision de [a,b]. On montre alors que I est une fonction lipschitzienne sur F, donc uniformément continue, donc se prolonge à l'adhérence de F dans E. Cette adhérence constitue l'espace des fonctions réglées, et contient les fonctions continues. On a défini ainsi l'intégrale de Riemann des fonctions réglées.
Approximation des fonctions continues par les polynômes
Soit f une fonction bornée sur [0,1]. Considérons la suite de polynômes :
Si f est continue en x, on montre que la suite (Pn(x)) converge vers f(x). Mais si f est continue sur [0,1] et donc uniformément continue, on montre que la suite (Pn) converge uniformément vers f sur [0,1]. Ce résultat constitue une version constructive du théorème de Weierstrass.
Image d'une suite de Cauchy
Soient E et F deux espaces métriques, et ![]() une application de
une application de ![]() vers
vers ![]() .
.
Si f est continue, alors l'image par f d'une suite convergente de E est une suite convergente de F.
Mais si f est uniformément continue, alors l'image par f d'une suite de Cauchy de E est une suite de Cauchy de F. Cette propriété est cruciale pour le théorème de prolongement des fonctions uniformément continues cité plus haut, et permet de le généraliser aux fonctions uniformément continues à valeurs dans un espace complet