Norme d'opérateur - Définition

En mathématiques, une norme d'opérateur ou norme subordonnée est une norme définie sur l'espace des opérateurs bornés entre deux espaces vectoriels normés.

Soient E et F deux espaces vectoriels normés, respectivement munis des normes et .

Soit f une application linéaire de E dans F.

Considérons

.

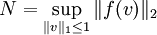Si , on dit que N est la norme de l'opérateur f, subordonnée à et .

Propriétés 

• Si 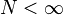, alors f est N-lipschitzienne et par conséquent continue. Réciproquement, si f est continue, alors  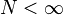: il existe ε > 0 tel que

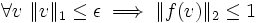
et par conséquent .

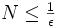• L'espace L(E,F) des fonctions linéaires continues de E dans F peut donc être muni de la norme subordonnée. Alors, pour tout v, 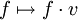est continue.
• Si E est de dimension finie, toute application linéaire de E dans un autre espace est continue.

Analyse approfondie

En analyse fonctionnelle, un opérateur linéaire borné est une application linéaire L entre espaces normés pour lesquels le rapport entre la norme L(v) et celle de v est borné lorsque v parcourt l'ensemble des vecteurs non nuls. Cela équivaut à la continuité de L pour les topologies induites par ces normes.

Dans le cas d'une matrice A représentant une application linéaire de R^m dans Rⁿ, ou de C^m dans Cⁿ, il est possible de montrer directement que A doit être bornée. En fait, la fonction

f(v) = ||A(v)||

est continue en tant que fonction de v, pour toute norme ||.|| et l'ensemble des vecteurs v de norme 1 est compact, comme partie fermée et bornée. La norme matricielle de A est par définition la borne supérieure de f. Dans ce cas, elle est atteinte pour des raisons de compacité.

Une norme d'opérateur satisfait les axiomes d'une norme (mathématiques), de sorte que l'ensemble des opérateurs linéaires bornés de V dans W est lui-même un espace normé. Il est complet si W est complet.

Il faut noter que deux normes distinctes interviennent ici : celle sur V et celle sur W. Même si V = W, il est possible de considérer deux normes distinctes sur ces espaces. En fait, pour deux normes ||.|| and |||.||| sur V, l'opérateur identité sur V a une norme d'opérateur, en passant de V muni de ||.|| à |||.|||, si et seulement s'il existe une constante C telle que, pour tout v :

|||v||| < C.||v||

Lorsque V est de dimension finie, cette propriété est garantie : par exemple, dans le cas de la dimension 2, les conditions ||v|| = 1 et |||v||| = 1 peuvent définir respectivement un rectangle et une ellipse, centrés en 0. Quelles que soient leurs proportions et orientations, on peut agrandir le rectangle en sorte que l'ellipse tienne à l'intérieur du rectangle agrandi et vice versa. Cependant, il s'agit d'un phénomène lié à la dimension finie car en dimension finie, toutes les normes sont équivalentes, c'est-à-dire sont majorées par un multiple constant de toute autre norme. Ceci entraîne entre autre leur équivalence topologique : toutes les normes définissent la même topologie, les mêmes ouverts. Mais en dimension infinie, ceci ne se vérifie pas. On peut le constater en considérant, par exemple, l'opérateur de dérivation D des polynômes trigonométriques. On peut prendre la racine carrée de la moyenne du carré comme norme : puisque D(e^inx) = ine^inx, les normes de D appliquée à des espaces de dimension finie de l'espace de Hilbert ne sont pas bornées. Un opérateur aussi simple que D peut ne pas avoir de norme d'opérateur.

Un théorème de base utilise le théorème de Baire pour montrer que si A a pour domaine et pour image un espace de Banach, alors A est borné. Pour l'exemple qui vient d'être donné, D ne peut pas être défini pour toutes les séries de Fourier de carré intégrable. En effet, nous savons, qu'elles peuvent représenter des fonctions continues mais nulle-part différentiables. L'intuition est que si A augmente les normes de certains vecteurs autant que ce qu'on veut, il est possible de condenser les singularités - choisir un vecteur v qui est la somme des autres et pour lequel ||L(v)|| ne pourrait pas être fini - ce qui montre que le domaine de A ne peut pas être V.

Norme d'un endomorphisme

Dans le cas où E = F, on choisit usuellement (même si ce n'est pas obligatoire) . Pour les normes usuelles, on dispose de formules pratiques : Prenons , notons un vecteur quelconque de et . On note A = (a_ij) la matrice de f dans la base canonique. On a alors :

• Si 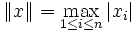, (norme infinie), alors la norme de f vaut :

• Si 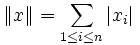, (norme indice 1), alors la norme de f vaut :

• Si 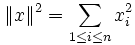, (produit scalaire canonique), alors le carré de la norme de f est égale au rayon spectral, c’est-à-dire la plus grande des valeurs absolue des valeurs propres de 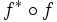où f ^* désigne l'adjoint de f.

Dans le cas particulier où f est un endomorphisme symétrique, la norme de f est égale au rayon spectral de f.

Norme duale

Dans le cas où muni de la valeur absolue. Pour chaque norme sur E, l'ensemble des formes linéaires continue de E, appelée dual topologique, peut ainsi être muni d'une norme.