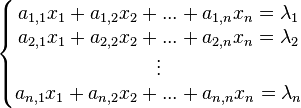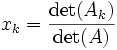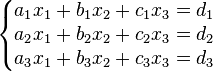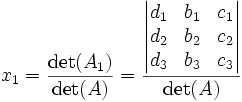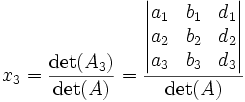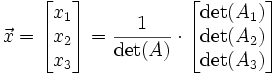Règle de Cramer - Définition
La règle de Cramer est un théorème en algèbre linéaire qui donne la solution d'un système d'équations linéaires en termes de déterminants.
En calcul, elle est généralement inefficace et donc n'est pas utilisée en applications pratiques qui pourraient impliquer plusieurs équations (utilisation de la méthode de résolution de Gauss). Cependant, elle est d'importance théorique pour la raison qu'elle donne une expression explicite pour la solution du système.
Elle est nommée d'après Gabriel Cramer, mathématicien suisse (1704-1752).
Description
Le système de n équations à n inconnues, de forme générale :
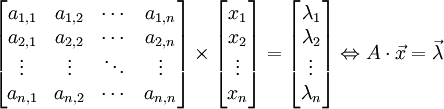
est représenté sous la forme d'un produit matriciel :
où la matrice A, carrée et inversible (déterminant non nul), contient les coefficients des inconnues, le vecteur colonne x contient ces inconnues et le vecteur colonne λ contient les membres de droite des équations du système.
Le théorème affirme alors que:
où Ak est la matrice carrée formée en remplaçant la kème colonne de A par le vecteur colonne ![]() .
.
Par extension, un système de Cramer est un système qui répond à la condition que le déterminant de la matrice A soit non nul.
- Le système admet une infinité de solutions si tous les déterminants des matrices du système sont nuls.
- Le système n'admet aucune solution si le déterminant de A est nul et qu'au moins un déterminant d'une matrice Ak est non nul.
Le nombre d'opérations à effectuer pour résoudre un système linéaire à l'aide de la règle de Cramer dépend de la méthode utilisée pour calculer le déterminant. Une méthode efficace pour les calculs de déterminant est l'élimination de Gauss-Jordan (complexité polynomiale). Cependant, la règle de Cramer demandera d'avoir recours à un nombre de calculs de déterminants égal à la taille du système, une élimination de Gauss-Jordan appliquée directement au système résout donc le problème plus efficacement.
Exemples
Système d'ordre 2
Soit :
alors :
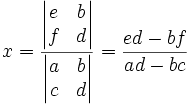 et
et 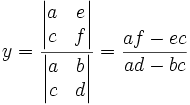
Exemple numérique :
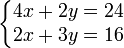
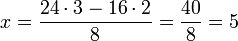 et
et 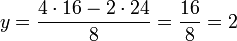
Système d'ordre 3
Soit :
Posons :
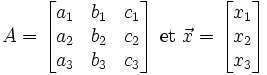 .
.
Le système admet une solution unique ssi ![]() :
:
Ou plus simplement :
Le système admet une infinité de solutions si :
Le système n'admet aucune solution si :