Théorème de Cayley-Hamilton - Définition
En algèbre linéaire, le théorème Cayley-Hamilton (qui porte les noms des mathématiciens Arthur Cayley et William Hamilton) affirme que tout endomorphisme d'un espace vectoriel de dimension finie sur un corps quelconque annule son propre polynôme caractéristique.
En terme de matrice, cela signifie que :
si A est une matrice carrée d'ordre n et si
![]()
est son polynôme caractéristique (polynôme d'indéterminée X), alors en remplaçant formellement X par la matrice A dans le polynôme, le résultat est la matrice nulle :
![]()
Le théorème de Cayley-Hamilton s'applique aussi à des matrices carrées à coefficients dans un anneau commutatif quelconque.
Un corollaire important du théorème de Cayley-Hamilton affirme que le polynôme minimal d'une matrice donnée est un diviseur de son polynôme caractéristique.
Motivation
Ce théorème possède deux familles d'utilisation:
- Il permet d'établir des résultats, théoriques, par exemple pour calculer le polynôme caractéristique d'un endomorphisme nilpotent.
- Il autorise aussi ces simplifications puissantes dans les calculs de matrices. L'approche par les polynômes minimaux est en général moins coûteuse que celle par les déterminants.
On trouve ce théorème utilisé dans les articles sur les polynômes d'endomorphisme, endomorphismes nilpotents, et plus généralement dans la théorie générale des matrices
Démonstration
Effectuons la démonstration sur la matrice A. Définissons la matrice B(X) = tcom(XI − A) (l'expression com(XI − A) désigne la comatrice de XI − A). On sait que
Nous pouvons interpréter les membres et facteurs de cette égalité comme des polynômes en X à coefficients dans l'anneau des matrices carrées nxn à coefficients dans K et cette égalité entraîne que P(X).I est divisible à gauche par XI − A. Ceci implique alors que la valeur à droite (égale en réalité ici aussi à sa valeur à gauche car on a tout aussi bien B(X).(XI − A) = det(XI − A).I) du polynôme P(X).I pour X = A est nulle. Cette valeur n'est autre que P(A), ce qui achève la démonstration.
Voir aussi Polynôme d'endomorphisme pour une autre démonstration.
Exemple
Considérons par exemple la matrice
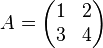 .
.
Le polynôme caractéristique s'écrit
Le théorème de Cayley-Hamilton affirme que
- A2 − 5A − 2I2 = 0
et cette relation peut être rapidement vérifiée dans ce cas. De plus le théorème de Cayley-Hamilton permet de calculer les puissances d'une matrice plus simplement que par un calcul direct. Reprenons la relation précédente
- A2 − 5A − 2I2 = 0
- A2 = 5A + 2I2
Ainsi, par exemple, pour calculer A4, nous pouvons écrire
- A3 = (5A + 2I2)A = 5A2 + 2A = 5(5A + 2I2) + 2A = 27A + 10I2
et il vient
- A4 = A3A = (27A + 10I2)A = 27A2 + 10A = 27(5A + 2I2) + 10A
- A4 = 145A + 54I2.
On peut également utiliser la relation polynomiale initiale A2 − 5A − 2I2 = 0 pour prouver l'inversibilité de A et calculer son inverse. Il suffit en effet de mettre en facteur une puissance de A là où c'est possible et
- A(A − 5I) = 2I2
ce qui montre que A admet pour inverse
