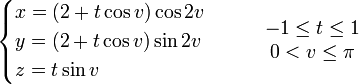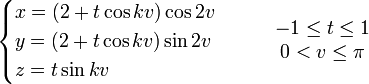Ruban de Möbius - Définition
Le ruban de Möbius est une curiosité topologique très facile à confectionner, comme le montre le schéma ci-dessous.
Il suffit d'utiliser une longue bande de papier, de lui faire subir une torsion d'un demi-tour puis de coller les deux extrémités. On découvre alors une surface ayant deux propriétés inattendues : cette surface ne possède qu'une seule face et qu'un seul bord. En mathématiques on parle de surface non orientable.
Si l'on coupe le ruban en deux dans le sens de la longueur, on obtient un anneau unique, vrillé, mais qui possède deux faces distinctes et deux bords distincts.
Si on le recoupe dans le sens de la longueur, on obtient... deux anneaux distincts, vrillés et entortillées l'un sur l'autre.
Cet objet a été conçu simultanément en 1858 par le mathématicien allemand August Ferdinand Möbius et par son compatriote Johann Benedict Listing, bien que ne travaillant pas ensemble.
Le nom du premier fut retenu grâce à un mémoire présenté à l'Académie des sciences à Paris.
On trouve également les dénominations de bande, anneau ou ceinture de Möbius ou de Moebius, notamment dans les traductions.
Le ruban de Möbius alimente également, de par sa particularité, des débats en philosophie. Les spéculations dont il peut faire l'objet ont ainsi inspiré le célèbre psychanalyste Jacques Lacan.
Définition par torsion d'une bande dans l'espace
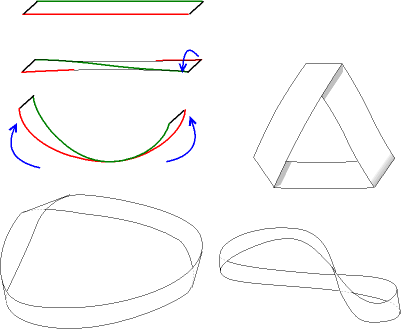
Confection du ruban
|
Schématisation du montage : recoller les deux flèches en respectant le sens
|
|---|
Ruban de Möbius classique
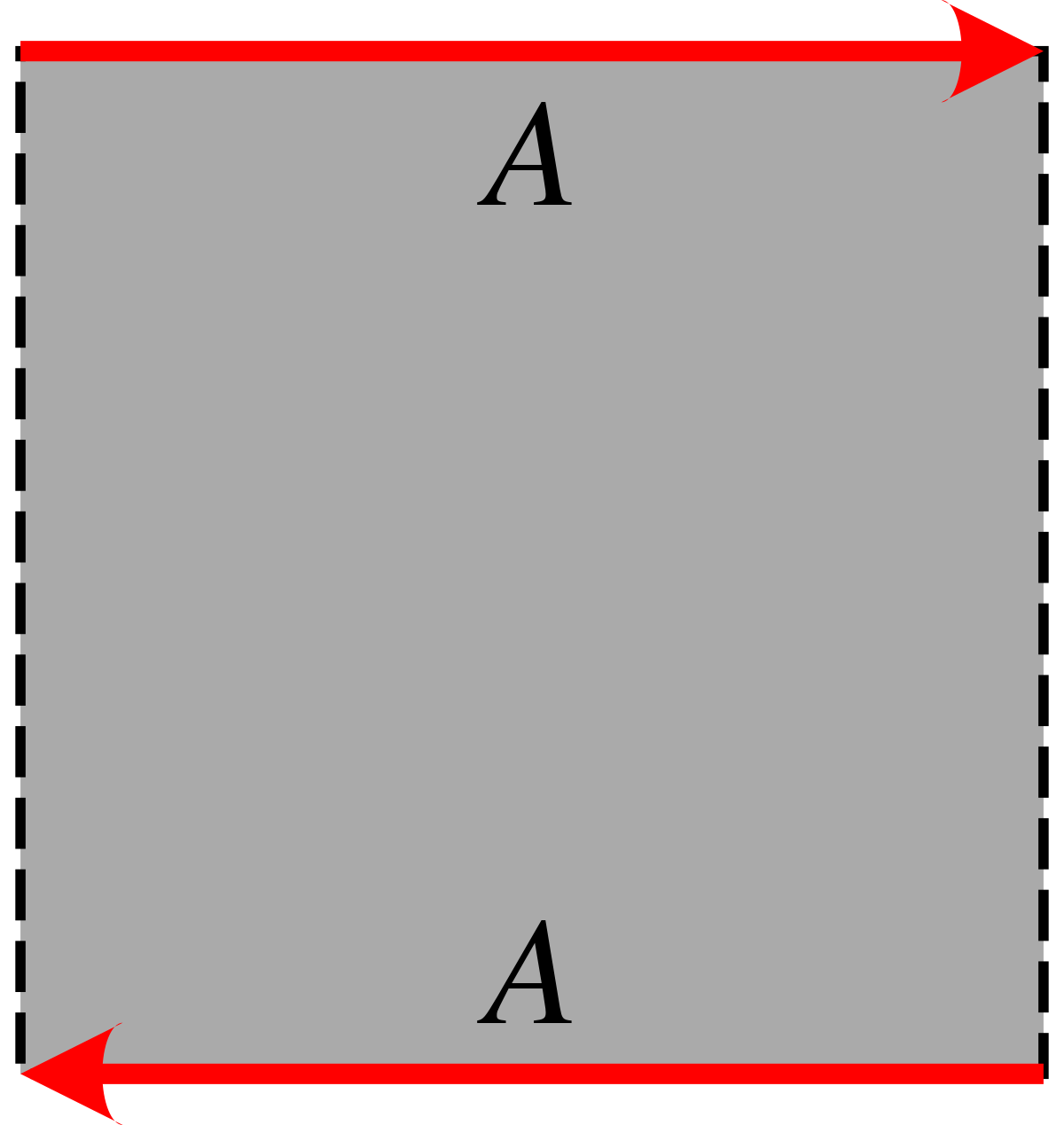
Le ruban de Möbius peut être engendré par un segment pivotant dont le centre décrit un cercle fixe. Un paramétrage correspondant est
Les courbes v = v0, t variant seul, sont bien des segments, reliant à vitesse uniforme le point v = v0, t = - 1 et le point v = v0, t = 1. Ce segment est donc de longueur 2.
La courbe t = 0 est un cercle de rayon 2 dans le plan horizontal ; elle représente la trajectoire du centre des segments. L'angle que fait le segment avec la direction horizontale est v0. Lorsque le centre a fait un tour complet sur le cercle horizontal (ajout de π à la varible v), le segment a fait un demi-tour seulement. Ce qui provoque le raccordement par exemple du point t = 1, v = π avec t = - 1, v = 0.
Le bord du ruban est donné par la courbe t = 1 ou t = - 1. Mais c'est la même courbe : le bord du ruban de Möbius est en un seul morceau (connexe).
Autres figures obtenues par torsion
Des variantes du ruban classique peuvent s'obtenir en faisant subir à la bande de papier un nombre impair de demi-tours de sens direct ou rétrograde. Il suffit d'ajuster le paramétrage précédent :
avec 
entier relatif impair.
Les figures obtenues pour k et -k sont énantiomorphes, c'est-à-dire des images miroirs l'une de l'autre.
Si l'on accepte des valeurs paires de k on obtient des rubans à deux faces, plus ou moins entortillés.
Comparaison des différents rubans
On peut s'intéresser à la courbe formant le bord de ces rubans. Elle a un entortillement différent pour chaque valeur de k. L'entortillement se calcule par exemple en projection (vue de dessus), en comptant le nombre de fois où la courbe passe au-dessus d'elle-même. On ne peut déformer continûment (c'est-à-dire par homotopie) un type de ruban en un autre dans l'espace de dimension 3.
Pourtant les différents rubans sont homéomorphes au ruban de Möbius classique, c’est-à-dire qu'il n'y a pas de différence intrinsèque entre eux. Celle-ci est liée à la façon dont ils sont plongés dans l'espace de dimension 3.
Le ruban de Möbius à un demi-tour peut également être vu comme une partie de la surface de Möbius.
Calcul de longueur du ruban
Le ruban de Möbius peut se réaliser avec un ruban flexible de l'épaisseur d'une feuille de papier de 70 gr par exemple. Pour obtenir un ruban sans pliage brusque, il faut que, pour une largeur de ruban égale à 1, la longueur soit supérieure à 1,732 - soit la racine carrée de 3. Il est possible d'aller vers plus petit en longueur jusqu'à faire se rejoindre, avec un renversement hélicoïdal, les côtés opposés d'un carré, mais les pliages seront brusques.
Définition par identification abstraite
Mathématiquement, on peut définir le ruban comme l'ensemble quotient de l'ensemble ![\R \times [-1,1] \,\!](https://static.techno-science.net/illustration/Definitions/autres/8/89740db8c954c205413c32a87f05c9d7_4062b4cf107d37af6c6deb92cffc0b44.png){kind=small}
par la relation d'équivalence définie par : 
si et seulement si 
, muni de la topologie quotient. Par comparaison, un ruban " normal " (tronc de cylindre) serait défini par la relation 
.
Cela permet de voir mathématiquement ce qui se passe quand on découpe le ruban : si ![p:\R \times [-1,1] \rightarrow \R \times [-1,1]/\Z](https://static.techno-science.net/illustration/Definitions/autres/7/74595cc80db7add62ff92dec898ea039_10088a9e8c1d481787a64b277238edfc.png){kind=small}
est l'application de passage au quotient, 
est un cercle dont le complémentaire est connexe.
On peut aussi réaliser le ruban de Möbius comme le complémentaire d'un disque ouvert dans le plan projectif réel (vu comme la sphère après idendification des points diamètralement opposés).
Symbolique
Une version schématisée du ruban de Möbius est utilisée comme logo des matières recyclables depuis le premier Jour de la Terre en 1970. La boucle Möbius indique qu'un produit peut être recyclé, ou qu'il a été fabriqué à partir de matériaux recyclés. Il s'agit en fait d'un ruban à trois demi-tours.
Adaptations artistiques
- Films
Thru the Moebius Strip, film entièrement numérique de 80 minutes réalisé par Frank Foster à Global Digital Productions (Hong Kong). Le film est sorti aux Etats-Unis en 2005.
- Séries
La particularité de ce phénomène a aussi été utilisée dans un épisode d'Ulysse 31.
Moebius est également le nom du double épisode final de la saison 8 de Stargate SG-1.
- Jeux Vidéo
- Mobius est également le "codename" du pilote, et accessoirement le héros que vous contrôlez dans le jeu Ace Combat 4 : Distant Thunder. Son nom de code complet est "Mobius 1", et son insigne personnel un ruban de Möbius.
- Mobius Ring est une course des jeux F-Zero AX et F-Zero GX sortis en Arcade et sur Gamecube.
- Romans
Dans 2010, Odyssée deux, l'aberration de comportement de l'ordinateur HAL 9000 est désignée comme une "boucle de Hofstadter-Möbius".
- Représentation
Un énorme anneau de Möbius est représenté sous forme de sculpture à Lille, dans le quartier de Wazemmes. Cette sculpture, créée par Marco Slinckaert occupe le centre d'un rond-point en face de la CPAM. Elle est aussi appelée serpent par sa grande ressemblance.
Maurits Cornelis Escher, graveur et dessinateur néerlandais (1898-1972), a fait de nombreuses études sur le ruban de Möbius.
La bande de Möbius outil de réflexion
Dans le vocabulaire de Jacques Lacan : 1962/63 - L'angoisse - 09/01/63 - Qu'est-ce qui fait qu'une image spéculaire est distincte de ce qu'elle représente ? c'est que la droite devient la gauche et inversement. - Une surface à une seule face ne peut pas être retournée. - Ainsi une bande de Mœbius, si vous en retournez une sur elle-même, elle sera toujours identique à elle-même. C'est ce que j'appelle n'avoir pas d'image spéculaire.