Calcul des propositions - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs est disponible ici.

Le calcul des propositions ou calcul propositionnel, dont le fondateur fut le logicien allemand Frege, version moderne de la logique stoïcienne, est une théorie logique qui définit les lois formelles du raisonnement. La notion de proposition est assez complexe à définir en général et a fait l'objet de nombreux débats au cours de l'histoire de la logique ; l'idée de base est qu'une proposition est un énoncé pour lequel il fait sens de parler de vérité.

En logique mathématique, le calcul des propositions définit les règles de raisonnement concernant les énoncés clos, c’est-à-dire ne dépendant d'aucun paramètre : par exemple, l'énoncé 3 est un nombre premier est un énoncé clos (une proposition atomique), alors que l'énoncé $p$ est un nombre premier, qui dépend du paramètre $p$ , n'en est pas un. Le calcul des propositions est une première étape dans la construction du calcul des prédicats, une formalisation complète du raisonnement mathématique.

D'un point de vue plus algébrique, le calcul de propositions (pour la logique classique) peut se voir comme un système de notations pour calculer dans les algèbres de Boole.

Introduction générale

Définition d'une proposition

Il est difficile de donner une définition consensuelle du concept de " proposition ". Une première approche (négative) consiste à dire ce qu'une proposition n'est pas. Ce n'est pas un énoncé assumé par un locuteur qui s'adresse à un autre locuteur précis dans un contexte particulier. Par exemple, un énoncé comme " je pense que… " étant une affirmation du locuteur n'est donc pas une proposition. Ou bien comme une proposition fait abstraction du contexte, les actes de langage accompagnant l'énoncé ou les indications renvoyant aux circonstances d'énonciation (tels les déictiques " ici " ou " maintenant ") ne sont pas pris en considération.

Ce qu'est une proposition: d'une part elle donne une information sur un état de chose: " 2 + 2 = 4 " ou " le livre est ouvert " pour prendre deux exemples très simples sont deux propositions en ce sens. De façon générale un état de chose peut être une vérité scientifique, un fait empiriquement observable, une formule mathématique. D'autre part une proposition peut être vraie ou fausse. C'est pourquoi une phrase optative (qui exprime un souhait comme par exemple " Que Dieu nous protège !") ou une phrase impérative (" viens !", " tais-toi !") ou une interrogation ne sont pas des propositions. " Que Dieu nous protège !" par exemple ne peut être ni vraie ni fausse: elle ne fait qu'exprimer un souhait du locuteur.

Définition d'un calcul

Un calcul en logique est un ensemble d'algorithmes c'est-à-dire de règles permettant en un nombre fini d'étapes, selon des règles explicites et selon des procédés mécanisables de déterminer si une proposition complexe (c'est-à-dire formée d'au moins deux propositions atomiques) est vraie ou fausse.

Le fait que la logique moderne grâce à Frege ait réussi à faire du traitement traditionnel des propositions depuis les stoïciens un calcul est sans doute ce qui constitue la nouveauté la plus importante de la logique moderne.

Structure

Comme la plupart des théories logico-mathématiques, il est possible de considérer le calcul des propositions des points de vue syntaxique et sémantique :

aspect syntaxique : il s'agit d'abord de définir le langage du calcul des propositions, les règles de formation des propositions complexes ainsi que les règles d'inférence permettant la déduction des propositions les unes à partir des autres. Ces règles de déduction sont choisies de façon à ce que les propositions engendrées soient effectivement des théorèmes. Dans le cadre d'une présentation axiomatique, on peut même partir d'une série de propositions primitives afin d'engendrer de nouvelles formules à partir de formules déjà produites.
aspect sémantique : on donne un sens aux symboles représentant les connecteurs logiques en fonction de la valeur de vérité des propositions de base (par exemple : $\lnot$ signifie non). Ce sens est donné, par exemple, par des tables de vérité.

La correspondance parfaite entre la déduction et la sémantique s'appelle la complétude.

Le système exposé ci-dessous se situe dans le cadre de la logique classique. On trouvera plus loin une présentation de logiques non classiques. L'adjectif " classique " ne doit pas être pris dans un sens de " normalité ", mais comme un attribut que lui a donné l'histoire de la logique, elle aurait tout aussi bien pu s'appeler " booléenne ".

Présentation

Syntaxe

La syntaxe du calcul des propositions comporte un alphabet associé à des règles de formation des formules et à des règles d'inférence. Nous présenterons dans la suite ces trois composantes : les deux composantes syntaxiques (formules et déductions) et la composante sémantique.

Le langage

Le langage du calcul des propositions est un langage formel et symbolique. Langage formel et symbolique dans la mesure où pour désigner les propositions on fait abstraction de la signification particulière des propositions (c'est l'étape de la formalisation) pour travailler uniquement avec des symboles comme les lettres p ou q appelées variables propositionnelles ou formules atomiques, notées p, q, etc., dans un ensemble infini, mais dénombrable, de symboles. À côté de ces lettres on utilise des parenthèses, éléments de ponctuation visant à lever les ambiguïtés dans les formules. À noter qu'on peut se passer des parenthèses en notation polonaise, inventée par le logicien polonais Jan ?ukasiewicz. Cependant à la suite, par exemple, de Christopher Strachey, les logiciens accordent de moins en moins d'attention à la syntaxe choisie pour se consacrer au fond des choses: la déduction et la sémantique.

Le deuxième élément fondamental du langage du calcul des propositions sont les opérateurs. Ce sont les symboles qui permettent de lier les propositions atomiques entre elles. Leur valeur est fonction de la valeur des propositions atomiques les composant. On dit pour cette raison que les opérateurs sont " vérifonctionnels ". Exemples de connecteurs logiques : et $\land$ , ou $\lor$ , non $\lnot$ , implique $\to$ , équivaut $\leftrightarrow$ , etc.

Un ensemble de connecteurs propositionnels est complet si tout connecteur peut se définir au moyen des connecteurs de l'ensemble. Par exemple l'ensemble $\{\neg, \to\}$ est complet et typiquement la disjonction se définit au moyen de la négation et de l'implication par : $A\lor B = \neg A\to B$ .

Il existe des présentations du calcul des propositions travaillant avec un nombre réduit de connecteurs: notamment l'ensemble constitué du seul connecteur d'incompatibilité de Sheffer, noté par une barre |. Il n'y a qu'un seul axiome :

(P | (Q | R)) | ((T | (T | T)) | ((S | Q) | ((P | S) | (P | S))))

Les connecteurs dérivés de la barre de Sheffer sont définis comme suit :

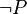$\lnot P$ a même signification que

P | P

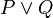$P \lor Q$ a même signification que

(P | P) | (Q | Q)

Veroff et McCune ont démontré en 2000 en utilisant leur système de démonstration automatique de théorèmes Otter que l'on peut formaliser le calcul propositionnel par la seule équation

((P | R) | Q) | ((P | (P | Q)) | P) = Q.

donc sans besoin de règle.

Les formules bien formées

Le calcul des propositions repose de plus sur des règles de formation indiquant comment construire des propositions complexes. Par exemple une proposition complexe comme " p q ? " n'est pas une proposition bien formée ou formule bien formée (" FBF " ou " well-formed formulae " en anglais) alors que " p ? q " est une " FBF ". De la même façon, à titre de comparaison, une phrase comme " je maison viens " n'est pas en français une phrase correctement construite.

Une formule ou énoncé bien formé est définie itérativement comme suit :

une variable propositionnelle p est une formule,
si $P$ et $Q$ sont des formules, alors 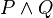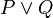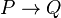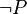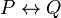$P \land Q$ , $P \lor Q$ , $P \to Q$ , $\lnot P$ , $P \leftrightarrow Q$ , etc. sont des formules.

EXEMPLES :

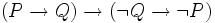$(P \to Q) \to (\lnot Q \to \lnot P)$ est une formule.

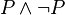$P \land \lnot P$ est une formule.

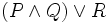$(P \land Q) \lor R$ est une formule.

$P \land Q \lor$ n'est pas une formule.

Formes normales conjonctives, formes normales disjonctives

Une expression est en forme normale conjonctive si elle est composée de conjonction de disjonction. Une expression est en forme normale disjonctive si elle est composée de disjonction de conjonction.

Exemple :

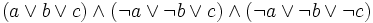$(a \lor b \lor c) \land (\lnot a \lor \lnot b \lor c) \land (\lnot a \lor \lnot b \lor \lnot c)$ est en forme normale conjonctive ;
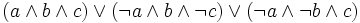$(a \land b \land c) \lor (\lnot a \land b \land \lnot c) \lor (\lnot a \land \lnot b \land c)$ est en forme normale disjonctive ;

La syntaxe comme théorie de la démonstration

L'élément le plus important de la syntaxe du calcul des propositions est cependant les règles de transformation des FBF. C'est l'élément le plus important dans la mesure où le calcul des propositions veut déterminer les règles de déduction d'une proposition à partir d'une autre. Or, le fait de déduire une proposition à partir d'une autre est assimilé par la logique à la transformation d'une proposition " A " en une proposition " B ". La syntaxe comme ensemble des règles de transformation peut donc être aussi dite théorie de la preuve. Ces règles de transformation sont composées de règles d'inférence voire d'axiomes dans le cas de la présentation axiomatique du calcul des propositions.

Une proposition déduite à partir d'une autre au moyen des règles d'inférence s'appelle un théorème. Dit autrement: Une formule qui admet une preuve est un théorème du calcul des propositions. Si $f$ est un théorème, on note cela par $\vdash f$ .

En logique classique une certaine tradition considère les deux connecteurs $\lnot$ (négation) et $\to$ (implication) comme primitifs. On donnera les règles de déduction pour eux seuls. Pour cela, on se donne trois schémas d'axiomes:

$f \to (g \to f)$

$(f \to (g \to h)) \to ((f \to g) \to (f \to h))$

$(\lnot f \to g) \to ((\lnot f \to \lnot g) \to f)$

où f, g, h peuvent être remplacés par des formules quelconques. La troisième formule est à la base du raisonnement par l'absurde.

On se donne également une règle d'inférence, le modus ponens, qui énonce que si $f$ et $f \to g$ sont des formules démontrées, alors $g$ est également démontrée.

Dans l'écriture de Sheffer, le modus ponens est remplacé par la règle d'inférence suivante :

si P et P | (Q | R) sont deux formules déjà prouvées, alors on peut déclarer R comme formule prouvée.

Soit $f$ une formule. Une preuve de $f$ est une liste finie et ordonnée de formules $f_1,\ldots,f_n$ avec $f n = f$ telle que chaque formule de la liste est ou bien

un axiome, ou bien
une formule qui est conséquence par modus ponens de formules antérieures de la liste.

Les trois axiomes et le modus ponens sont donc les règles de base du raisonnement logique, desquelles on peut déduire toutes les autres règles de raisonnement.

Exemples de théorèmes

Nous indiquons ci-dessous une liste de théorèmes qu'on peut démontrer à l'aide des règles précédentes, ainsi que le nom usuel qui leur est attribué par la tradition.

$A \to A$	identité
$A \lor \lnot A$	tiers exclu
$\lnot\lnot A \leftrightarrow A$	double négation
$((A \to B) \to A) \to A$	loi de Peirce
$\lnot(A \land \lnot A)$	loi de non-contradiction
$\lnot(A \land B) \leftrightarrow (\lnot A \lor \lnot B)$	lois de De Morgan
$\lnot(A \lor B) \leftrightarrow (\lnot A \land \lnot B)$	lois de De Morgan
$(A \to B) \to(\lnot B \to \lnot A)$	contraposition
$((A \to B) \land A)\to B$	modus ponens
$((A \to B) \land \lnot B) \to \lnot A$	modus tollens
$((A \to B) \land (B \to C)) \to (A \to C)$	modus barbara
$(A \land (B \lor C)) \leftrightarrow ((A \land B) \lor (A \land C))$	distributivité
$(A \lor (B \land C)) \leftrightarrow ((A \lor B) \land (A \lor C))$	distributivité

Donnons un exemple de preuve du théorème de double négation (ou du moins d'une des deux implications), en supposant prouvé le théorème d'identité et le modus barbara :

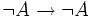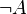(1) $\lnot A \to \lnot A$ (identité appliquée sur $\lnot A$ )

(2) 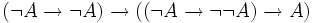$(\lnot A \to \lnot A) \to ((\lnot A \to \lnot \lnot A) \to A)$ (axiome 3 sur

A

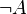et $\lnot A$ )

(3) 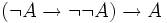$(\lnot A \to \lnot \lnot A) \to A$ (modus ponens entre (1) et (2))

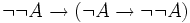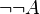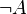(4) $\lnot \lnot A \to (\lnot A \to \lnot \lnot A)$ (axiome 1 avec $\lnot \lnot A$ et $\lnot A$ )

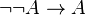(5) $\lnot \lnot A \to A$ (modus barbara entre 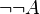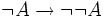$\lnot \lnot A$ , $\lnot A \to \lnot \lnot A$ et

A

)

Donc $\vdash \lnot \lnot A \to A$ . Cette formule prouvée est équivalente à $\lnot A \lor A$ qui est la propriété du tiers exclu.

Voir déduction naturelle pour d'autres exemples de preuves.

Sémantique

La sémantique est seconde par rapport à la syntaxe car les seules propositions bien formées peuvent être douées de sens. La sémantique ou théorie des modèles détermine les règles d'interprétations des formules. Attribuer des valeurs de vérité à chacune des propositions élémentaires intervenant dans la formule A revient à choisir un modèle de cette formule

De façon plus précise, l'interprétation d'une formule est le fait d'attribuer une valeur aux propositions simples et aux connecteurs (en fonction de la valeur des propositions simples). Il existe alors trois cas d'interprétation:

Quand il n'y a que des 0, c'est une antilogie ou contradiction. C'est la négation de la tautologie. On dit également que A est insatisfiable.
S'il y a au moins un 1 et au moins un 0, c'est une formule synthétique ou contingente.
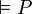Lorsque le résultat n'est constitué que de 1, c'est une loi logique ou tautologie. On dira que A est une formule valide, et on notera $\vDash P$ .

Les tables de vérités développées originellement par Wittgenstein sont un exemple d'une interprétation d'une formule mathématique.

Exemples d'interprétation des connecteurs:

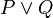$P \lor Q$ prendra la valeur 1 si et seulement si au moins l'une des deux propositions P ou Q prend la valeur 1.

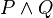$P \land Q$ prendra la valeur 1 si et seulement si les deux propositions P et Q prennent simultanément la valeur 1.

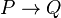$P \to Q$ prendra la valeur 0 si et seulement si P prend la valeur 1 et Q la valeur 0.

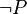$\lnot P$ prendra la valeur 1 si et seulement si P prend la valeur 0.

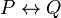$P \leftrightarrow Q$ prendra la valeur 1 si et seulement si P et Q ont la même valeur.

Exemple 1 :

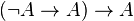$(\lnot A \to A) \to A$ est une tautologie.

En effet, si on attribue à A la valeur 0, alors $\lnot A$ prend la valeur 1, $(\lnot A \to A)$ prend la valeur 0, et $(\lnot A \to A) \to A$ prend la valeur 1. De même, si on attribue à A la valeur 1, alors $\lnot A$ prend la valeur 0, $(\lnot A \to A)$ prend la valeur 1, et $(\lnot A \to A) \to A$ prend la valeur 1.

Exemple 2 :

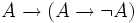$A \to (A \to \lnot A)$ n'est pas une tautologie.

En effet, si on attribue à A la valeur 1, alors $\lnot A$ prend la valeur 0, $A \to \lnot A$ prend la valeur 0, et $A \to (A \to \lnot A)$ prend la valeur 0.

Le calcul propositionnel dispose donc de deux moyens différents pour valider les formules : la méthode axiomatique qui définit les formules prouvées, et la méthode des valeurs de vérité qui définit les tautologies.

Principales propriétés

Décidabilité, cohérence, complétude

Le fait que toute formule est prouvable si et seulement si elle est une tautologie exprime le fait que le calcul propositionnel est complet. La présentation déductive du calcul propositionnel est donc équivalent à la présentation sémantique. En effet :

Toute formule prouvée résulte d'un axiome ou de l'application du modus ponens sur des formules déjà prouvées. Or il est facile de vérifier que les trois schémas d'axiomes fournissent des tautologies, et que le modus ponens conserve les tautologies. Toute formule prouvée est donc une tautologie. Le calcul propositionnel est correct.
La réciproque repose sur le fait suivant: on peut démontrer que pour toute formule $P$ du calcul propositionnel il existe une formule $P'$ telle que 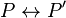$P \leftrightarrow P'$ et telle que $P'$ soit sous une forme dite normale 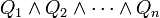$Q_1 \land Q_2 \land \cdots \land Q_n$ où chaque $Q i$ est de la forme 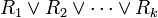$R_1 \lor R_2 \lor \cdots \lor R_k$ , avec chaque $R i$ atomique (de la forme $p$ ou 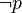$\lnot p$ ). Si $P'$ est une tautologie, alors dans chaque $Q i$ , apparaissent nécessairement une variable propositionnelle $p$ et sa négation 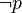$\lnot p$ . Sinon il existerait $Q i$ qui ne vérifierait pas cette condition et il serait possible d'attribuer des valeurs aux $p j$ de façon à donner la valeur 0 à $Q i$ , et donc à $P'$ lui-même. Mais on peut montrer que 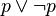$p \lor \lnot p$ est prouvable ( 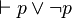$\vdash p \lor \lnot p$ ), puis qu'il en est de même de chaque $Q i$ , puis de $P'$ lui-même et enfin de $P$ . Toute tautologie est alors prouvable. Le calcul propositionnel est complet.

Voir le théorème de complétude du calcul des propositions pour une autre démonstration, plus détaillée.

Il résulte de la complétude du calcul des propositions que :

Le calcul propositionnel est décidable, dans le sens où il existe un algorithme permettant de décider si une formule est un théorème ou non. Il suffit de dresser sa table de vérité et de voir s'il s'agit d'une tautologie.
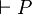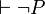Le calcul propositionnel est cohérent (consistant), c'est-à-dire non contradictoire. Il n'existe aucune formule P telle qu'on puisse avoir en même temps $\vdash P$ et $\vdash \lnot P$ car ces deux propositions seraient des tautologies et on aurait 1 = 0.
Le calcul propositionnel est fortement complet (maximalement cohérent), dans le sens où tout ajout d'un nouveau schéma d'axiome, non prouvable dans le système initial, rend ce système incohérent.

Méthodes de calcul, NP-complétude

Nous avons vu que, pour décider si une formule est prouvable, il suffit de vérifier si c'est une tautologie, c'est-à-dire de vérifier si elle prend la valeur de vérité 1 quelles que soient les valeurs de vérité de ses atomes.

Cette approche théorique se heurte cependant au temps de calcul que demande une telle démarche. En effet, si la formule possède n variables propositionnelles atomiques, il faudra calculer 2ⁿ valeurs possibles de la formule complète, ce qui devient rapidement difficile pour n trop grand. Ainsi, si n = 30, il faudra vérifier plus d'un milliard de valeurs. Si n = 100, le temps de calcul nécessaire pour effectuer toutes les vérifications dépasse de loin l'âge de l'Univers.

Il existe certes des améliorations possibles. Par exemple, si on attribue la valeur de vérité 0 à une variable propositionnelle A, on peut attribuer directement la valeur 0 à $A \land B$ indépendamment de la valeur ultérieure attribuée à B, ce qui diminue le nombre de calculs à effectuer.

On peut également chercher à voir s'il est possible d'invalider les implications. Considérons par exemple la formule :

$((p \to (q \land r \land s))\land \lnot s) \to \lnot p$

Étant constituée d'une implication, pour la rendre invalide, il suffit que la conclusion $\lnot p$ puisse prendre la valeur 0 (et donc $p$ la valeur 1) et que l'hypothèse $((p \to (q \land r \land s))\land \lnot s)$ puisse prendre la valeur 1 (et donc $\lnot s$ et $p \to (q \land r \land s)$ la valeur 1). Mais alors $s$ prend la valeur 0 et $(p \to (q \land r \land s)$ ne peut plus prendre que la valeur 0. Il est donc impossible d'invalider l'implication et celle-ci est une tautologie.

Mais les améliorations précédentes ne changent pas fondamentalement la difficulté du problème. On est donc devant la situation suivante. Étant donnée une formule f, on se demande si f est une tautologie ou non et pour cela, on se demande s'il existe des valeurs de vérité attribuables aux atomes de f qui rendraient f invalide.

Une recherche exhaustive demande 2ⁿ vérifications si f possède n variables propositionnelles atomiques. Cette démarche est dite déterministe, mais son temps de calcul est exponentiel.
Par contre, si f n'est pas une tautologie, il suffit d'une vérification à faire, à savoir tester précisément la configuration qui invalide f. Le temps de calcul cesse d'être exponentiel, à condition de savoir quelle configuration tester. Celle-ci pourrait par exemple être recherchée par tirage au sort. Une telle démarche est dite non déterministe.

On dit alors que la question de l'insatisfiabilité de f est du type NP (pour polynomial non déterministe). Le problème dual est celui de la satisfiabilité d'une formule, à savoir trouver une configuration qui donne 1 comme valeur de vérité de la formule. Cette question, appelée problème SAT joue un rôle fondamental en théorie de la complexité, puisqu'on peut montrer que la découverte d'un algorithme déterministe en temps polynomial pour ce problème permettrait d'en déduire des algorithmes déterministes en temps polynomial pour tous les problèmes de type NP. On dit que SAT (et donc également le problème de la prouvabilité d'une formule) est un problème NP-complet.

Compacité

La compacité du calcul propositionnel réside dans la propriété suivante. Supposons donné un nombre infini de formules. On se pose la question de savoir si ces formules sont simultanément satisfiables, c'est-à-dire s'il existe des valeurs de vérité de leurs atomes qui donne 1 comme valeur de vérité à toutes les formules. On montre que, si tel est le cas pour tout sous-ensemble fini de ces formules, alors il en est de même pour toutes les formules. On renvoie à l'article théorème de compacité pour plus d'information.

Algèbre de Boole

Soit donné un ensemble de variables propositionnelles atomiques. Soit E l'ensemble des formules ayant pour atomes ces variables propositionnelles. Soit $\mathfrak R$ la relation binaire définie sur E par l'équivalence ( $\leftrightarrow$ ) entre deux formules. $\mathfrak R$ est une relation d'équivalence sur E, compatible avec $\lor$ et $\land$ . Alors l'ensemble quotient E/ $\mathfrak R$ possède une structure d'algèbre de Boole.

Systèmes de démonstration formelle

Il existe plusieurs familles de systèmes de démonstration formelle, notamment:

les systèmes à la Hilbert,
la déduction naturelle
et le calcul des séquents.

Procédure d'évaluation des lois

Il existe plusieurs procédés pour décider si une formule est antilogique (fausse pour toute interprétation), consistante (vraie pour au moins une interprétation) ou bien une tautologie.

Les tables de vérité sont un de ces procédés.
La méthode de résolution de Herbrand qui se base sur les expressions en forme normale conjonctive.
La méthode de résolution qui provient des tableaux sémantiques de Evert Willem Beth.

Logique classique, minimale, intuitionniste

La logique classique et le tiers exclu

Les axiomes du calcul propositionnel que nous avons présentés sont ceux de la logique classique. Ils permettent de prouver la formule $P \lor \lnot P$ , appelée principe du tiers exclu, la formule $\lnot\lnot P \to P$ , appelée élimination de la double négation, ou la formule $((P \to Q) \to P) \to P$ appelée loi de Peirce. Cette logique repose sur le principe qu'une propriété P est nécessairement vraie ou fausse. C'est le point de vue, qualifié de formaliste, adopté par Hilbert. Or ce point de vue a été contesté par plusieurs mathématiciens, dont le plus connu est Brouwer, créateur de la logique intuitionniste. Essayons de comprendre pourquoi.

Pour Hilbert, il suffit de prouver qu'une propriété P n'entraîne aucune contradiction pour justifier la validité de P. En effet, P n'entraîne aucune contradiction peut être représenté en calcul propositionnel sous la forme suivante (en désignant par $\bot$ une contradiction du type $Q \land \lnot Q$ ) :

$\lnot(P \to \bot)$

ce qui, en logique classique, est équivalent à :

$\lnot(\lnot P \lor \bot)$

et donc à :

$\lnot \lnot P \land \lnot \bot$

Compte tenu que $\lnot \bot$ est un théorème, on a :

$\lnot \lnot P$

et puisque $\lnot \lnot P \to P$ est aussi un théorème, on obtient

P

Si P formule par exemple l'existence d'un objet mathématique, on voit que, pour Hilbert, il suffit que cette existence n'entraîne aucune contradiction pour pouvoir être validée, quand bien même on ne disposerait d'aucun procédé pour mettre en évidence l'objet ainsi introduit. En d'autres termes, l'implication classique se réduit à l'implication matérielle $P \vee \neg P.$ Pour les intuitionnistes, l'existence d'une demonstration repose sur un procédé constructif pour la fabriquer à partir des axiomes.

Les mathématiciens intuitionnistes ou constructivistes ne peuvent que rejeter la démarche évoquée ci-dessus, et en particulier la dernière étape $\lnot \lnot P \to P$ . Ils n'introduisent donc pas dans leur calcul des propositions le troisième axiome du calcul propositionnel classique relatif à la négation. Cette démarche, jugée marginale dans la première moitié du XXème siècle, a pris depuis un intérêt grandissant, pour deux raisons. Primo, la logique intuitionniste se situant "avant" la logique classique permet de mieux comprendre cette dernière. Secundo, la nature calculatoire de la logique intuitionniste allié à la correspondance de Curry-Howard fait de celle-ci la logique la mieux adaptée à l'informatique. Certes des travaux récents des logiciens contemporains parviennent à conférer aussi à la logique classique un contenu calculatoire, mais son caractère plus complexe le fait sortir des limites de cet article.

Logique minimale, logique intuitionniste

Nous présentons deux variantes très proches de logique non classique, la logique minimale de Johansson ^? (1936) et la logique intuitionniste de Heyting (1930). Les connecteurs primitifs sont $\to$ , $\land$ , $\lor$ et $\lnot$ . On garde les deux premiers axiomes de la logique classique :

$f \to (g \to f)$

$(f \to (g \to h)) \to ((f \to g) \to (f \to h))$

Avant d'introduire la négation, on énonce les axiomes relatifs à $\land$ :

$(f \land g) \to f$

$(f \land g) \to g$

$(f \to g) \to ((f \to h) \to (f \to (g \land h)))$

et ceux relatifs à $\lor$ , (duaux des précédents) :

$f \to (f \lor g)$

$g \to (f \lor g)$

$(f \to h) \to ((g \to h) \to ((f \lor g) \to h))$

On introduit enfin deux axiomes relatifs à la négation. Le premier exprime que, si f prouve sa propre négation, alors f est invalide.

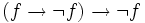$(f \to \lnot f) \to \lnot f$ .

Le second définit le comportement de chaque logique vis-à-vis d'une contradiction, et la seule différence entre la logique minimale et la logique intuitionniste porte sur cet axiome.

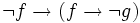$\lnot f \to (f \to \lnot g)$ pour la logique minimale, et 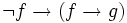$\lnot f \to (f \to g)$ pour la logique intuitionniste.

En présence d'une formule et de sa négation, les trois logiques, classique, intuitionniste et minimale, concluent toutes trois à une contradiction $\bot$ . Mais la différence porte sur l'utilisation que l'on fait de cette contradiction :

La logique classique déduit de 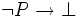$\lnot P \to \bot$ le fait que P est vrai (raisonnement par l'absurde).
La logique intuitionniste déduit d'une contradiction que toute formule est prouvable. De 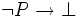$\lnot P \to \bot$ , elle déduit la validité de 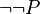$\lnot\lnot P$ , propriété plus faible que $P$ .
La logique minimale déduit d'une contradiction que toute négation de formule est prouvable, qui est plus faible que ce que propose la logique intuitionniste.

Logique minimale et logique intuitionniste acceptent le théorème $\lnot (f \land \lnot f)$ . Par contre $f \lor \lnot f$ n'est pas un théorème de ces logiques.

De même, elles permettent de prouver $f \to \lnot \lnot f$ mais pas la réciproque. Par contre, elles prouvent l'équivalence entre $\lnot f$ et $\lnot \lnot \lnot f$ . Enfin, la formule $(\lnot f \lor g) \to (f \to g)$ est un théorème de la logique intuitionniste, mais pas de la logique minimale.

Glivenko a démontré en 1929 que $f$ est un théorème du calcul propositionnel classique si et seulement si $\lnot \lnot f$ est un théorème du calcul propositionnel intuitionniste. Ce résultat est faux en calcul propositionnel minimal, ainsi d'ailleurs qu'en calcul des prédicats intuitionniste.

Grande avancée sur la compréhension de l'origine des tumeurs

Il y a 8 heures

La malbouffe consommée à l'adolescence a des impacts irréversibles sur la mémoire

Il y a 8 heures

Batteries: capacité triplée avec ces nouvelles anodes en silicium !

Il y a 13 heures

La moelle épinière possède sa propre mémoire

Il y a 13 heures

Cette équation prédit une "magnetic RAM" un million de fois plus rapide

Il y a 15 heures

Des humains ont vécu dans cet immense tube de lave il y a 7000 ans

Il y a 15 heures

L'anxiété et la dépression peuvent diminuer grâce à cette stimulation transcrânienne

Il y a 1 jour

Le bon ratio oméga-6/oméga-3 dans l'assiette pour lutter contre l'obésité

Il y a 1 jour

Des particules plus rapides que la lumière ? Premier test réussi pour les tachyons

Il y a 1 jour

Cette nouvelle approche permet de cibler les cellules cancéreuses pour les combattre

Il y a 1 jour

Intel dévoile le plus grand ordinateur neuromorphique au monde, imitant le cerveau humain

Il y a 1 jour

Cette créature expliquerait notre réaction instinctive de combat ou de fuite

Il y a 1 jour

Les traumatismes de l'enfance altèrent les fonctions musculaires en vieillissant

Il y a 2 jours

Pourquoi nous gratouillons-nous si souvent pour rien ?

Il y a 2 jours

Découverte d'un serpent géant, le plus grand de tous les temps ?

Il y a 2 jours

Découverte d'un nouveau principe de mouvement dans les cristaux liquides

Il y a 2 jours

Une concentration extrême de matière noire révélée par cet anneau d'Einstein

Il y a 2 jours

Comment les émissions des véhicules à essence se transforment en particules respirables

Il y a 2 jours

L'atmosphère de Vénus fuit dans l'espace

Il y a 3 jours

Quand la lutte contre la pollution de l'air contribue au réchauffement climatique: le paradoxe environnemental

Il y a 3 jours

Un trou noir dormant géant découvert dans notre voisinage cosmique

Il y a 3 jours

Grippe aviaire: le risque de propagation aux humains "extrêmement préoccupant" d'après l'OMS

Il y a 3 jours

Le secret des crânes coniques et des dents limées des Vikings

Il y a 3 jours

Les terres rares, loin d'être rares, affectent les plantes

Il y a 3 jours

La marine américaine développe sa première arme à micro-ondes contre les drones

Il y a 4 jours

Premier atlas de l'ovaire humain: un pas vers l'ovaire artificiel

Il y a 4 jours

La vision suffit pour produire les mouvements collectifs (vidéo)

Il y a 4 jours

Comment la Voie lactée a-t-elle influencé l'Egypte antique ?

Il y a 4 jours

Coopérer ou rivaliser: comment décide notre cerveau ?

Il y a 4 jours

S'inspirer des os de géants pour la construction

Il y a 5 jours

Rigidité artérielle: un nouvel indicateur pour prévenir les maladies cardiovasculaires

Il y a 5 jours

Pourquoi les femmes seules consomment-elles plus de sucreries ?

Il y a 5 jours

Que faut-il savoir sur les PFAS, ces "polluants éternels" ?

Il y a 5 jours

Découverte: ces substances courantes accélèrent le vieillissement

Il y a 6 jours

Des scientifiques identifient le meilleur moment de la journée pour faire du sport

Il y a 6 jours

Cette rupture technologique pourrait décupler la capacité des disques durs

Il y a 6 jours

Cycle menstruel: une étude scientifique établit un lien avec la Lune

Il y a 6 jours

Quand un trio d'étoiles devient un couple: une histoire cataclysmique retracée

Il y a 6 jours

Ce petit ver possède des yeux immenses: pourquoi ?

Il y a 6 jours

D'où vient cette structure fractale observée dans une bactérie ?

Il y a 7 jours

Découverte majeure dans les allergies respiratoires

Il y a 7 jours

Voici ce qui a produit la lumière la plus lumineuse jamais détectée dans l'Univers

Il y a 7 jours

Propagation inquiétante de la "mouche noire" suceuse de sang en Allemagne

Il y a 7 jours

Le hasard confère le prix Turing et 1 million de dollars au mathématicien Avi Wigderson

Il y a 7 jours

AI Act: comment encadrer l'intelligence artificielle en Europe ?

Il y a 7 jours

Quelle est cette forme étrange photographiée près de la Lune ?

Il y a 8 jours

Si vous avez déjà eu une entorse de la cheville, attention à ceci

Il y a 8 jours

Démonstration d'une nouvelle technologie de lévitation, stable et sans supraconductivité

Il y a 8 jours

Ces indices d'une rupture imminente de la faille de San Andreas

Il y a 8 jours

Cet effet inattendu de la musculation sur la mémoire

Il y a 8 jours

Populaires

Découverte d'un serpent géant, le plus grand de tous les temps ?

Des particules plus rapides que la lumière ? Premier test réussi pour les tachyons

Batteries: capacité triplée avec ces nouvelles anodes en silicium !

Grande avancée sur la compréhension de l'origine des tumeurs

Cette équation prédit une "magnetic RAM" un million de fois plus rapide

La malbouffe consommée à l'adolescence a des impacts irréversibles sur la mémoire

Toutes les ventes flash et Codes Promos Amazon

Cdiscount: les meilleures réductions actuelles

Page générée en 6.249 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales | Partenaire: HD-Numérique
Version anglaise | Version allemande | Version espagnole | Version portugaise