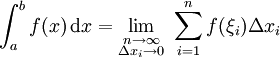Intégrale de Riemann - Définition
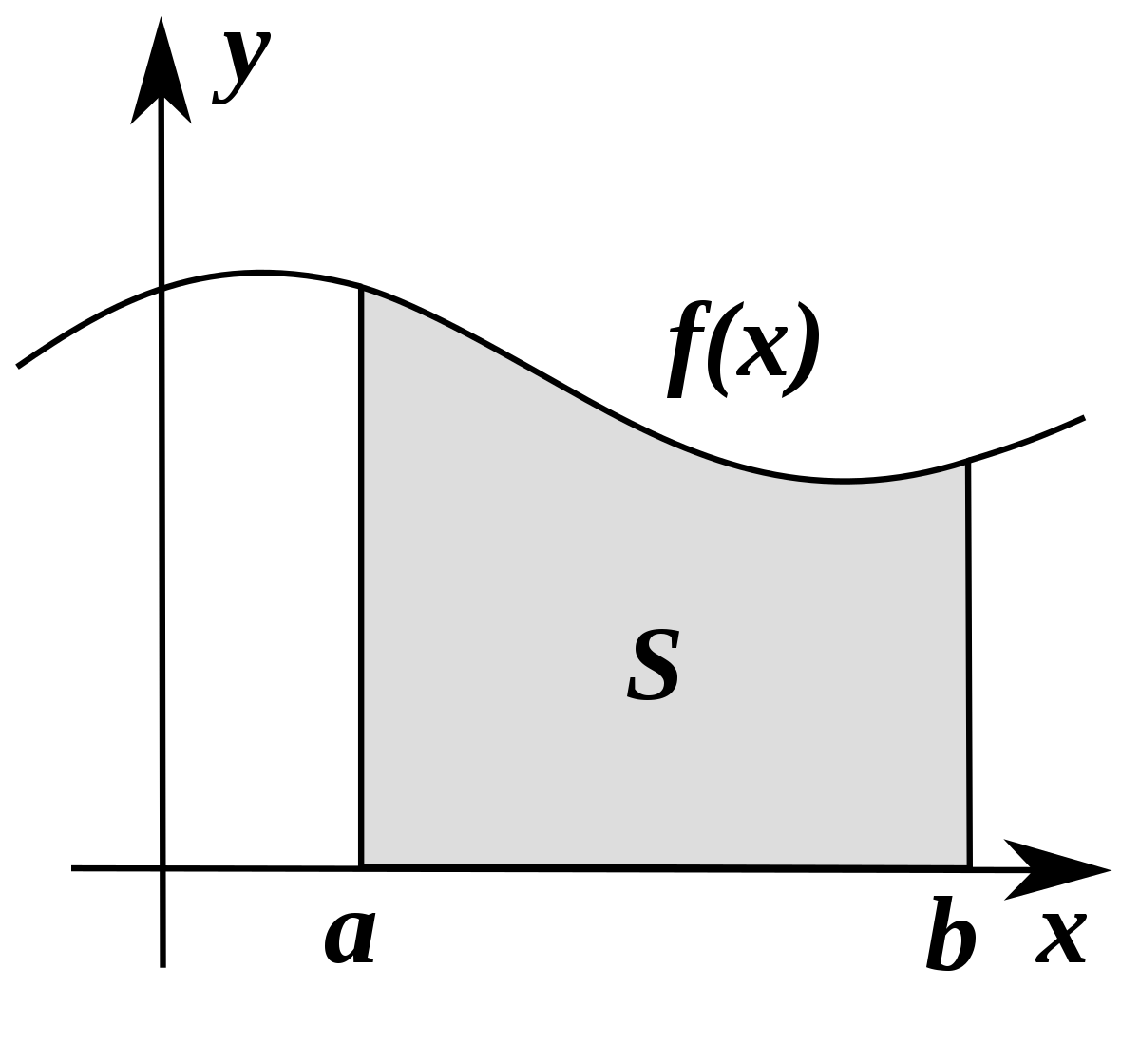
En analyse réelle, l'intégrale de Riemann est une façon simple de définir l'intégrale d'une fonction sur un intervalle. En termes géométriques, cette intégrale s'interprète comme l'aire du domaine sous la courbe représentative de la fonction, comptée algébriquement.
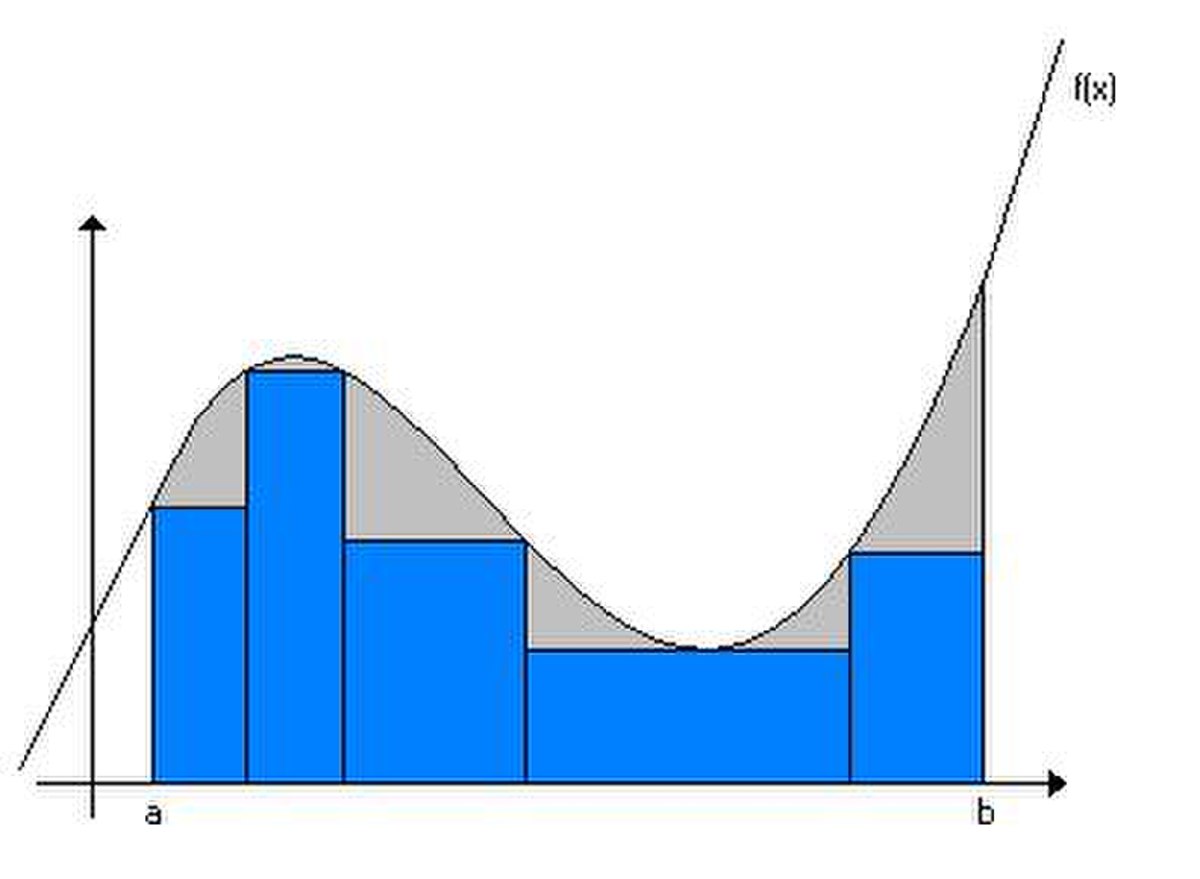
Le procédé général utilisé pour définir l'intégrale de Riemann est l'approximation par des fonctions en escalier, pour lesquelles la définition de l'aire sous la courbe est aisée. Les fonctions pour lesquelles cette définition est possible sont dites intégrables au sens de Riemann. C'est le cas notamment des fonctions continues, continues par morceaux, ou réglées sur un segment [a,b].
On obtient un procédé d'intégration plus général et plus satisfaisant, notamment vis-à-vis du passage à la limite, en introduisant l'intégrale de Lebesgue.
Définition de l'intégrale
Les fonctions en escalier
Soit E un sous-ensemble quelconque du segment [a,b]. Soit χE la fonction qui vaut 1 si x appartient à E et 0 si x n'appartient pas à E. χE est appelée la fonction indicatrice de E, ou la fonction caractéristique de E.
Ces fonctions sont notre point de départ et nous posons :
- pour tout segment [c,d] inclus dans [a,b] et pour toute constante z≥0,
![\int z \chi_{[c,d]}(x)\,\mathrm d x = z(d-c)](https://static.techno-science.net/illustration/Definitions/autres/4/4b651bc2e76c289da1af97e63d7107b5_4bfb9275940616edbf7aedb2c4fb3d7f.png) .
.
Dans ce cas l'aire sous la courbe de cette fonction est égale à l'aire du rectangle de base [c,d] et de hauteur z.
De la même manière, quelques expérimentations géométriques avec de telles fonctions nous amènent à penser que si f1, f2,..., f n sont n fonctions indicatrices sur des intervalles disjoints et si a1,a2,...,an sont des scalaires positifs, alors l'aire du domaine sous la courbe de la fonction
doit être égale à
Une fonction de cette forme est appelée une combinaison linéaire de fonction indicatrices, ou tout simplement une fonction en escalier. Remarquons maintenant que nous avons décidé quelle devrait être l'intégrale d'une fonction en escalier.
Nous prenons un raccourci maintenant en déclarant que la formule précédente reste valable si certains coefficients aj sont négatifs.
Une différence cruciale entre l'intégrale de Riemann et celle de Lebesgue, est que les fonctions en escalier de l'intégrale de Lebesgue sont des combinaisons linéaires de fonctions indicatrices sur des ensembles qui ne sont pas nécessairement des intervalles.
Bien sûr, nous devons travailler d'avantage pour pouvoir calculer des intégrales d'une plus grande classe de fonctions que celle des fonctions en escalier. Aussi remarquons que l'intégrale de Lebesgue n'utilise pas de sommes supérieures, et que les fonctions positives sont traitées en premier, avant d'étendre l'intégrale aux fonctions qui peuvent prendre des valeurs négatives.
Définition générale
Soit f continue sur [a;b]. Soit ![]() une subdivision de [a;b] (avec x0 = a et xn = b), ξi tel que
une subdivision de [a;b] (avec x0 = a et xn = b), ξi tel que ![]() et Δxi = xi − xi − 1 :
et Δxi = xi − xi − 1 :
Fonctions à valeurs réelles : intégrales inférieure et supérieure
À partir d'observations géométriques, simplement en voyant que le domaine Sf[réf. nécessaire] est un sous-ensemble de Sg[réf. nécessaire] (Au moins dans le cas de fonctions positives, ceci est clair.), nous imposons que si f vérifie pour tout x de [a,b], f(x)≤g(x) alors
Nous appelons cette propriété la croissance de l'intégrale.
L'intégrale d'une fonction en escalier étant définie et la condition de monotonie étant imposée, nous pouvons intégrer des fonctions à valeurs positives arbitraires. Soit f une fonction à valeurs réelles définie sur [a,b] et soit l une fonction en escalier telle que pour tout x on ait, l(x)≤f(x). De plus, soit u une fonction en escalier telle que pour tout x on ait, u(x)≥f(x). Si nous devions donner une valeur à ∫ f conforme à la condition de monotonie, alors nous devrions avoir :
L'intégrale ∫l est alors appelée une somme inférieure pour f et l'intégrale ∫u est alors appelée une somme supérieure pour f. L'inégalité précédente doit être vérifiée pour toutes sommes supérieures et inférieures de f, donc nous pouvons en déduire une autre inégalité:
où supl∫l est la borne supérieure de toutes les sommes inférieures, et infu∫u est la borne inférieure de toutes les sommes supérieures (voir borne supérieure et borne inférieure.) Le nombre supl∫l est parfois appelé intégrale inférieure de f; de la même manière, le nombre infu∫u est appelé intégrale supérieure.
Si les intégrales supérieures et inférieures sont égales, alors il y a seulement une façon de définir ∫ f. Il ne peut pas arriver que l'intégrale inférieure soit plus grande que l'intégrale supérieure (par construction, comme le lecteur peut le vérifier.) Cependant, il peut arriver que l'intégrale supérieure ne soit pas égale à l'intégrale inférieure. Par exemple, le lecteur peut vérifier cela, pour la fonction indicatrice :
- χQ
où Q est l'ensemble des nombres rationnels du segment [a,b] avec a<b, l'intégrale inférieure est égale à 0 et l'intégrale supérieure est égale à b-a>0.
Toutes les fonctions dont les intégrales inférieures et supérieures sont finies et égales, constituent l'ensemble des fonctions intégrables au sens de Riemann ou Riemann-intégrables. En revanche, les fonctions qui ont des intégrales inférieures et supérieures différentes sont dites non intégrables au sens de Riemann. Dans le contexte de cet article, nous dirons intégrable ou non intégrable sachant que nous parlons d'" intégrabilité " au sens de Riemann.
On peut vérifier qu'une fonction en escalier a une intégrale égale à ses intégrales supérieures et inférieures.
Propriétés
Ceci peut être démontré à partir des premiers principes de la construction de l'intégrale de Riemann.
La preuve repose sur le fait qu'une fonction continue sur un segment est uniformément continue.
La condition f bornée ne peut pas être omise.
Les hypothèses du théorème 4 (convergence uniforme sur un segment) sont très fortes. Une première difficulté avec l'intégrale de Riemann se pose, lorsque nous tentons d'amoindrir ces hypothèses. En fait, la suite numérique (∫fk) converge vers le nombre ∫f plus souvent que le théorème le suggère, mais il est très difficile de le prouver dans cet ensemble. La meilleure façon d'avoir un théorème plus fort est d'utiliser l'intégrale de Lebesgue.
Un autre problème avec l'intégrale de Riemann est qu'elle ne s'étend pas aux intervalles non bornés très facilement. Si nous souhaitons intégrer une fonction f de -∞ à +∞, nous pouvons calculer
Cependant, certaines propriétés (telles que l'invariance par translation, le fait que l'intégrale de Riemann ne change pas si nous translatons l'intégrande f) ne sont plus vérifiées. En fait, le Théorème 4 devient faux pour une telle intégrale, et il devient très difficile d'utiliser des limites conjointement avec l'intégrale. De telles intégrales sont appelées intégrales impropres. À nouveau, l'intégration de Lebesgue allège ces difficultés.