Transformée de Fourier - Définition
En analyse, la transformation de Fourier est un analogue de la théorie des séries de Fourier pour les fonctions non périodiques, et permet de leur associer un spectre en fréquences. On cherche ensuite à obtenir l'expression de la fonction comme " somme infinie " des fonctions trigonométriques de toutes fréquences qui forment son spectre. Une telle sommation se présentera donc sous forme d'intégrale. L'analyse non standard permet de la présenter sous forme d'une série et justifie le point de vue intuitif. Séries et transformation de Fourier constituent les deux outils de base de l'analyse harmonique.
La transformée de Fourier 
est une opération qui transforme une fonction intégrable en une autre fonction, décrivant le spectre en fréquences de f. Si f est une fonction intégrable, sa transformée de Fourier est la fonction F(f) et donnée par la formule
L'ensemble de départ est l'ensemble des fonctions intégrables f d'une variable réelle x. L'ensemble d'arrivée est l'ensemble des fonctions F(f) d'une variable réelle s. Concrètement lorsque cette transformation est utilisée en traitement du signal, on dit que x est la variable temps, que f est dans le domaine temporel, que s est la fréquence et que F est dans le domaine fréquentiel.
La formule dite de transformation de Fourier inverse, opération notée TF -1, est celle qui permet (sous conditions) de retrouver f à partir du spectre :
En physique, la transformation de Fourier permet de déterminer le spectre d'un signal. Les phénomènes de diffraction donnent une image de l'espace dual du réseau, ils sont une sorte de " machine à transformation de Fourier " naturelle.
Le cadre le plus naturel pour définir les transformées de Fourier est celui des fonctions intégrables. Toutefois, de nombreuses opérations (dérivations, transformée de Fourier inverse) ne peuvent être écrites en toute généralité. On doit à Plancherel l'introduction de la transformation de Fourier pour les fonctions de carré sommable, pour lesquelles la formule d'inversion est vraie. Puis la théorie des distributions de Schwartz permit de trouver un cadre parfaitement adapté.
Transformation de Fourier pour les fonctions intégrables
Si f est une fonction intégrable sur 
, sa transformée de Fourier est donnée par la formule
F est aussi parfois notée 
ou TF(ƒ).
La transformée de Fourier se généralise à de nombreux groupes, on peut citer les groupes abéliens localement connexes (cf Dualité de Pontryagin) ou plus simplement les groupes abéliens finis (cf analyse harmonique sur un groupe abélien fini). La base utilisée n'est plus celles des fonctions exponentielles imaginaires mais les éléments du groupe dual.
Propriétés
- cette transformation est linéaire
- la transformée de Fourier de f est une fonction continue, de limite nulle à l'infini (théorème de Riemann-Lebesgue), notamment bornée par
- par changement de variable on trouve des formules intéressantes lorsqu'on effectue une translation, dilatation du graphe de f
- la transformée de Fourier d'une gaussienne est une gaussienne.
- on peut tenter d'appliquer un théorème de dérivation sous intégrale : si la fonction g(x)=-ixf(x) est elle aussi intégrable, alors la dérivée de
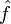est la transformée de Fourier de g. - si f est dérivable, de limite nulle à l'infini, et f intégrable, alors
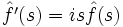est la transformée de Fourier de f.
On peut résumer les deux dernières propriétés : sous conditions d'existence, la transformation de Fourier échange dérivation et multiplication par (plus ou moins) ix. C'est justement pour s'affranchir de ces conditions d'existence désagréables qu'il sera nécessaire d'élargir la classe des fonctions sur lesquelles opère la transformation de Fourier.
Inversion de Fourier
Si la transformée de Fourier de f est elle-même une fonction intégrable :
Cette opération de transformation de Fourier inverse a des propriétés analogues à la transformation directe, puisque seuls changent le coefficient multiplicatif et le -i devenu i.
Soit f est une fonction de classe 
à support compact. Par le principe de transfert, on peut se contenter d'étudier le cas d'une fonction standard. Dans ce cas, il existe un réel infiniment grand T tel que pour tout réel | x | > T, f(x) = 0. Introduisons une base orthonormée totale de l'espace de Hilbert L2([ − T,T]) donnée par :
Par le lemme de Parseval, on est en mesure d'écrire :
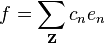où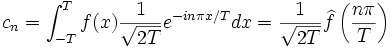 
Plus explicitement :
La dernière égalité vient de ce que la somme de Riemann s'effectue sur une partition de longueur infiniment petite (π / T). L'égalité recherchée est donc vraie pour toutes les fonctions standards de classe à support compact. Par le principe de transfert, elle est aussi vérifiée pour toutes les fonctions à support compact et de suite par densité pour toutes les fonctions intégrables dont la transformée est intégrable.
Extension à l'espace 
Si f est une fonction intégrable sur , sa transformée de Fourier est donnée par la formule
L'intégrale est prise sur l'espace entier et le point désigne le produit scalaire entre s et x.
Si la transformée de Fourier de f est elle-même une fonction intégrable :
Transformation de Fourier pour les fonctions de carré sommable
Le théorème de Plancherel permet d'étendre la transformation de Fourier aux fonctions de carré sommable. On se place donc sur l'espace de fonctions 
, muni de sa norme canonique. Pour des raisons qui apparaîtront claires, on modifie légèrement la convention sur la transformée de Fourier dans cette section.
Soit f une fonction de carré sommable sur et soit A>0. On peut définir la transformée de Fourier de la fonction tronquée à [-A, A] :
Alors lorsque A tend vers l'infini, les fonctions 
convergent en moyenne quadratique vers une fonction qu'on note et que l'on appelle transformée de Fourier (ou de Fourier-Plancherel) de f.
En outre la formule d'inversion de Fourier est vérifiée : la fonction est elle-même de carré sommable et
![f = \lim\limits_{\|\;\|_2} \left[x\mapsto \frac1{\sqrt{2\pi}}\, \int_{-A}^{A} \hat{f}(w)\, e^{iwx}\, dw\right]](https://static.techno-science.net/illustration/Definitions/autres/e/e7efe4cfba3bf239596dfe77d405e44f_795990c8074cc3a5d3b023964c64d503.png){kind=small}
Ainsi la transformation de Fourier-Plancherel définit un automorphisme de l'espace L2, qui est une isométrie
En physique, on interprète le terme 
figurant sous l'intégrale comme une densité spectrale de puissance.
La définition de la transformation de Fourier-Plancherel est compatible avec la définition habituelle de la transformée de Fourier des fonctions intégrables. En effet, On peut montrer que l'application 
prolonge l'application qui a une fonction f, intégrable, associe sa transformée de Fourier. On se place alors sur l'espace 
sur lequel la transformée de Fourier est bien définie et qui est dense dans 
. Comme est un espace de Banach, on a l'unicité de 
.