Loi de Bernoulli - Définition
| Densité de probabilité / Fonction de masse |
|
| Fonction de répartition |
|
| Paramètres | |
| Support | |
| Densité de probabilité (fonction de masse) | |
| Fonction de répartition | 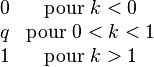 1 \end{matrix}" /> 1 \end{matrix}" /> |
| Espérance | |
| Médiane (centre) | non disponible |
| Mode | |
| Variance | |
| Asymétrie (skewness) | |
| Kurtosis (non-normalisé) | |
| Entropie | |
| Fonction génératrice des moments | |
| Fonction caractéristique | |
En mathématiques, la distribution de Bernoulli ou loi de Bernoulli, du nom du mathématicien suisse Jacques Bernoulli, est une distribution discrète de probabilité, qui prend la valeur 1 avec la probabilité p et 0 avec la probabilité q = 1 − p.
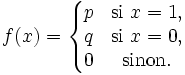
L'espérance mathématique d'une variable aléatoire de Bernoulli vaut p et la variance vaut pq = p(1 − p).
Le Kurtosis tend vers l'infini pour des valeurs hautes et basses de p, mais pour p = 1 / 2 la distribution de Bernoulli a un kurtosis plus bas que toute autre distribution, c’est-à-dire 1.
La distribution de Bernoulli s'applique lors d'une épreuve de Bernoulli dont le succès est 1 et l'échec 0.
Distributions liées
- Si
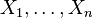 sont des variables aléatoires de Bernoulli avec paramètre p, indépendantes identiquement distribuées,alors
sont des variables aléatoires de Bernoulli avec paramètre p, indépendantes identiquement distribuées,alors 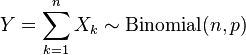
(Loi binomiale).
Populaires