Bijection - Définition
Une fonction f: X → Y est dite bijective ou est une bijection si pour tout y dans l’ensemble d'arrivée Y il existe un et un seul x dans l’ensemble de définition X tel que f(x) = y. On dit encore dans ce cas que tout élément y de Y admet un unique antécédent x (par f).
De manière équivalente, une bijection est une fonction qui est à la fois injective et surjective. Les bijections sont aussi appelées des applications biunivoques. Cantor a le premier démontré que, s'il existe une injection de X vers Y et une injection de Y vers X, alors il existe une bijection entre les deux ensembles (voir Théorème de Cantor-Bernstein).
Lorsque X et Y sont tous les deux égaux à la droite réelle ![]() , une fonction bijective
, une fonction bijective ![]() a un graphe qui intersecte toute droite horizontale en exactement un point.
a un graphe qui intersecte toute droite horizontale en exactement un point.
Si X et Y sont des ensembles finis, alors il existe une bijection entre les deux ensembles X et Y ssi X et Y ont le même nombre d’éléments. La généralisation de cela aux ensembles infinis mène au concept de cardinal d’un ensemble, une façon de distinguer les différentes tailles d’ensembles infinis.
Définition formelle
Soit f une application de E dans F. f est bijective si et seulement si ![]()
Exemple concret
Prenons le cas d'une station de vacances où un groupe de touristes doit être logé dans un hôtel. Chaque façon de répartir ces touristes dans les chambres de l'hôtel peut être représentée par une application de l'ensemble des touristes vers l'ensemble des chambres (à chaque touriste est associée une chambre).
- Les touristes souhaitent que l'application soit injective, c'est-à-dire que chacun d'entre eux ait une chambre individuelle. Cela n'est possible que si le nombre de touristes ne dépasse pas le nombre de chambres.
- L'hôtelier souhaite que l'application soit surjective, c'est-à-dire que chaque chambre soit occupée. Cela n'est possible que s'il y a au moins autant de touristes que de chambres.
- Ces desiderata sont incompatibles si le nombre de touristes est différent du nombre de chambres. Dans le cas contraire, il sera possible de répartir les touristes de telle sorte qu'il y en ait un seul par chambre, et que toutes les chambres soient occupées : l'application sera alors à la fois injective et surjective ; on dira qu'elle est bijective.
Exemples et contre-exemples
Considérons la fonction ![]() définie par f(x) = 2x + 1. Cette fonction est bijective, puisque pour tout nombre réel arbitraire donné y, nous pouvons trouver exactement une solution réelle de l’équation y = 2x + 1 d’inconnue x à savoir x = (y − 1)/2.
définie par f(x) = 2x + 1. Cette fonction est bijective, puisque pour tout nombre réel arbitraire donné y, nous pouvons trouver exactement une solution réelle de l’équation y = 2x + 1 d’inconnue x à savoir x = (y − 1)/2.
D’un autre côté, la fonction ![]() définie par g(x) = x2 n’est pas bijective, pour essentiellement deux raisons différentes. La première est que, nous avons (par exemple) g(1) = 1 = g(−1), et donc g n’est pas injective; la seconde est qu’il n’y a (par exemple) aucun nombre réel x tel que x2 = −1, et donc g n’est pas surjective non plus.
définie par g(x) = x2 n’est pas bijective, pour essentiellement deux raisons différentes. La première est que, nous avons (par exemple) g(1) = 1 = g(−1), et donc g n’est pas injective; la seconde est qu’il n’y a (par exemple) aucun nombre réel x tel que x2 = −1, et donc g n’est pas surjective non plus.
L’une ou l’autre de ces constatations est suffisante pour montrer que g n’est pas bijective.
D’autre part, si nous définissons la fonction ![]() par la même relation que g, mais avec les ensembles de définition et d’arrivée restreints à
par la même relation que g, mais avec les ensembles de définition et d’arrivée restreints à ![]() , alors la fonction h est bijective.
, alors la fonction h est bijective.
L’explication est que, pour un nombre réel positif donné y, nous pouvons trouver exactement une solution réelle positive de l’équation y = x2 qui est x = √y.
Propriétés
- Une fonction f: X → Y est bijective si et seulement s’il existe une fonction g: Y → X telle que
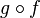 soit l’application identique sur X et
soit l’application identique sur X et 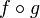 soit l’application identique sur Y. Les bijections sont précisément les isomorphismes dans la catégorie des ensembles. Dans ce cas, g est déterminée de manière unique par f et nous appelons g l’application réciproque de f et nous écrivons f −1 = g. De plus, g est aussi une bijection, et la réciproque de g est f à nouveau.
soit l’application identique sur Y. Les bijections sont précisément les isomorphismes dans la catégorie des ensembles. Dans ce cas, g est déterminée de manière unique par f et nous appelons g l’application réciproque de f et nous écrivons f −1 = g. De plus, g est aussi une bijection, et la réciproque de g est f à nouveau. - Si f o g est bijective, alors f est surjective et g est injective.
- Si f et g sont toutes deux bijectives, alors f o g est aussi bijective.
- Si X est un ensemble, alors les fonctions bijectives de X sur lui-même, forment avec l’opération de composition des applications (
 ), un groupe, le groupe des permutations de X, qui est noté indifféremment S(X), SX, σX ou σ(X).
), un groupe, le groupe des permutations de X, qui est noté indifféremment S(X), SX, σX ou σ(X).
...----...