Ensemble fini - Définition
En mathématiques, un ensemble E est dit fini si et seulement si E est vide ou s'il existe un entier n et une bijection de E dans l'ensemble des n premiers entiers naturels.
On note alors le nombre d'éléments de E, ou la cardinalité de E :
- Card(E) = n
- #E = n
- |E| = n
Par convention, l'ensemble vide a pour cardinal 0.
E est fini au sens de Dedekind s’il n'est pas infini, c'est-à-dire si et seulement s'il ne peut pas être mis en bijection avec l'une de ses parties strictes (ou encore : toute injection de E dans lui-même est surjective). E fini implique E fini au sens de Dedekind, mais la réciproque nécessite l'axiome du choix.
Caractérisation
Nous noterons | [a;b] | l'ensemble ![]() .
.
Si F est en bijection avec E, un ensemble fini non vide, alors F est non vide, et card(E) = card(F).
- En effet, E est fini, donc en notant n son cardinal, il existe
![f : |[ 1 ; n ]| \rightarrow E](https://static.techno-science.net/illustration/Definitions/autres/a/a48dcdc0bdc508daa449be8fe568888c_726329b3250b448bb57d2d098db3e29b.png) une bijection, et par hypothèse, il existe
une bijection, et par hypothèse, il existe 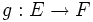 .
. - La composée de bijections est une bijection, donc
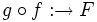 est bijective.
est bijective. - Donc F est fini car en bijection avec les n premiers entiers naturels, et card(F) = n.
Parties
Soit ![]() , E un ensemble fini de cardinal n, a un élément de E (qui existe car E non vide).
, E un ensemble fini de cardinal n, a un élément de E (qui existe car E non vide). ![]() est fini de cardinal n - 1.
est fini de cardinal n - 1.
- Si n = 1, alors E = {a}, donc
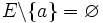 qui est fini, et
qui est fini, et 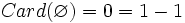 .
. - Si
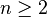 , alors il existe
, alors il existe ![h : |[1 ; n ]| \rightarrow E](https://static.techno-science.net/illustration/Definitions/autres/f/f6ab7aa0da351a16b9fa7451e6cffd2d_557c64302ccfe8859f44a1c118b4c317.png) une bijection.
une bijection.
- Si h(n) = a, alors
![\tilde h : |[1 ; n-1 ]| \rightarrow E \backslash \{a\}](https://static.techno-science.net/illustration/Definitions/autres/f/ff0d390a357ca0a01b04547238a6deb3_0fa63c122b3b79893d69a6c8e0d71da2.png) est encore bijective, donc
est encore bijective, donc 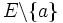 est fini de cardinal n − 1.
est fini de cardinal n − 1. - Si
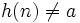 , alors par bijectivité de h, il existe un unique l tel que
, alors par bijectivité de h, il existe un unique l tel que 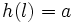 .
. - On considère
![\begin{matrix} \sigma : & |[1 ; n]| \rightarrow |[1 ; n ]| & \ \\ \ & \sigma(k) = k & \forall k \in |[1 ; n ]| \backslash \{l ; n \} \\ \ & \sigma(l) = n & \ \\ \ & \sigma(n) = l & \ \end{matrix}](https://static.techno-science.net/illustration/Definitions/autres/9/91cfd25624bd7e56fac7514a9c7711e3_9dd15bfcdab3cbadf9ad24b19ed063e2.png)
![\sigma \circ \sigma = \operatorname{id}_{|[1 ; n ]|}](https://static.techno-science.net/illustration/Definitions/autres/e/ef5ba8d65a2efb85689693ffc5ad0503_858b175752114a6f4152d87f7abd29e2.png) , donc σ est bijective.
, donc σ est bijective.![h \circ \sigma : |[1 ; n]| \rightarrow E](https://static.techno-science.net/illustration/Definitions/autres/7/776d4ea5790a3bf251637e83c5d7851d_acd3b36e74105bf70243eed94d93ebc4.png) est bijective comme composée, et
est bijective comme composée, et 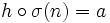 . On s'est ramené au cas précédent, et
. On s'est ramené au cas précédent, et 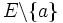 est fini de cardinal n − 1.
est fini de cardinal n − 1.
- Si h(n) = a, alors
Toute partie d'un ensemble fini est finie.
- La démonstration se fait par récurrence avec ce qui précède.
Opérations
La réunion d'ensembles finis est finie. Plus précisément, si A et B sont deux ensembles finis, alors ![]() et
et ![]() sont finis, et
sont finis, et ![]() .
.