Détermination orbitale - Définition
Le processus préliminaire de détermination orbitale consiste à déterminer à partir d'observations, les six éléments orbitaux qui décrivent l'orbite d'un corps céleste :
- Ω, longitude du nœud ascendant
- i, inclinaison du plan de l'orbite sur le plan fondamental
- a, demi grand axe
- e, excentricité
- ω, angle du périastre
- t0, un des temps de passage au périastre
La difficulté de ce procédé découle du fait qu'une observation nous donne uniquement la direction du corps céleste par rapport à l'observateur et aucune information quant à la distance qui sépare ce corps de l'observateur.
La position de l'objet dans l'espace est alors inconnue et les composantes de la vitesse de ce même objet sont également indéterminées. Il est alors nécessaire d'effectuer des observations supplémentaires à d'autres moments pour augmenter la quantité d'information disponible.
Considérons les coordonnées cartésiennes héliocentriques ![]() du corps céleste. Celles-ci sont liées aux éléments orbitaux par les relations :
du corps céleste. Celles-ci sont liées aux éléments orbitaux par les relations :
Les membres de droites de ces équations comportent tous les éléments orbitaux. ![]() et ω apparaissent explicitement alors que
et ω apparaissent explicitement alors que ![]() et t0 sont représentés indirectement au travers des variables :
et t0 sont représentés indirectement au travers des variables :
- r, distance de l'astre, et
- v, angle du rayon astre-corps en orbite avec l'axe principal de l'ellipse, orienté vers le périastre.
Le passage des coordonnées héliocentriques écliptiques aux coordonnées géocentriques écliptiques s'effectue par les relations :
où X,Y,Z sont les coordonnées écliptiques géocentriques du Soleil i.e des paramètres connus et ![]() sont les coordonnées géocentriques écliptiques du corps céleste
sont les coordonnées géocentriques écliptiques du corps céleste
où λ et β sont la longitude et la latitude du corps respectivement et ρ représente la distance du corps céleste à la Terre i.e la distance géocentrique qui est un paramètre inconnu. Cependant, les positions apparentes d'un corps céleste sont habituellement obtenues en mesurant les écarts angulaires par rapport aux étoiles voisines supposées fixes. Puisque les positions des étoiles sont cataloguées en ascension droite et déclinaison, i.e les coordonnées géocentriques équatoriales, les résultats des observations d'un corps céleste sont également donnés dans ces coordonnées. Il est alors nécessaire de passer du repère équatorial au repère écliptique. Cette transition s'effectue à l'aide des relations trigonométriques suivantes (trigonométrie sphérique).
où ε correspond à l'inclinaison du plan équatorial par rapport à l'écliptique. Ces dernières équations nous donnent :
Cette dernière équation permet de déterminer la longitude λ. On déduit également la latitude β. Par substitutions, on obtient :
Notons que la distance héliocentrique r est liée à la distance géocentrique ρ. Ces équations représentent donc un système de trois équations à sept inconnues, les six éléments orbitaux et la distance géocentrique ρ ; les autres quantités, ![]() et
et ![]() étant toutes connues. Ce système n'admettant pas de solution unique, on peut se poser la question de savoir quel est le nombre minimal d'observations qu'il est nécessaire d'effectuer pour être en mesure de résoudre le problème de la détermination orbitale d'un corps céleste.
étant toutes connues. Ce système n'admettant pas de solution unique, on peut se poser la question de savoir quel est le nombre minimal d'observations qu'il est nécessaire d'effectuer pour être en mesure de résoudre le problème de la détermination orbitale d'un corps céleste.
Nombre minimum d'observations
Nous venons de voir qu'une observation menée en un temps t1 nous amenait à résoudre un système de trois équations à sept inconnues, à savoir:
Il est alors évident que deux observations menées aux temps t1 et t2 nous mèneront à un système de six équations à huit inconnues
et de manière analogue, trois observations nous donneront un système de neuf équations à neuf inconnues
Dès lors, pour obtenir les éléments orbitaux, il est nécessaire d'effectuer une série de trois observations.
![\begin{matrix} x &=& r[\cos(v+\omega)\cos \Omega -\sin(v+\omega)\sin\Omega\cos i] \\ y &=& r[\cos(v+\omega)\sin\Omega+\sin(v+\omega)\cos\Omega\cos i] \\ z &=& r\sin(v+\omega)\sin i \end{matrix}](https://static.techno-science.net/illustration/Definitions/autres/b/b1a65e4ab6f7430faccdd461798620d1_448e08553032104db250b02a36cb1893.png)
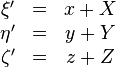
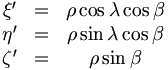
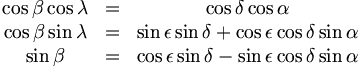
![\begin{matrix} \rho\cos\lambda\cos\beta &=& r[\cos(v+\omega)\cos\Omega -\sin(v+\omega)\sin\Omega\cos i]-X \\ \rho\sin\lambda\cos\beta &=& r[\cos(v+\omega)\sin\Omega -\sin(v+\omega)\cos\Omega\cos i]-Y \\ \rho\sin\beta &=& r\sin(v+\omega)\sin i-Z \end{matrix}](https://static.techno-science.net/illustration/Definitions/autres/d/d9b7e8d0ff1d66da4bbe719811233fc6_9261cf094056bc5af724044cc98c661e.png)