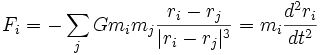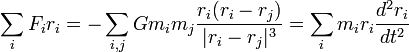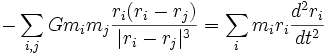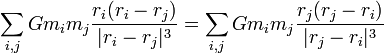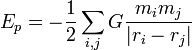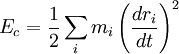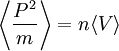Théorème du viriel - Définition
Le théorème du viriel est un théorème physique qui énonce que :
- 2Ec + Ep = 0.
Ce résultat est une simple conséquence du principe fondamental de la dynamique, appliqué à un ensemble de masses en interaction gravitationnelle réciproque (problème à N corps).
L'énergie totale E = Ec + Ep vaut donc
.
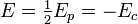Il peut aussi être généralisé à d'autres domaines, sous la forme
- 2Ec = a·Ep
où a est la puissance de r dans l'expression de Ep ; on retrouve bien la forme précitée car a vaut -1 pour la force gravitationnelle.
Démonstration
En dynamique à N-corps
- Hypothèse
- un système de N corps massifs isolé ; chaque corps ne subit donc que les seules forces gravitationnelles de ses voisins.
Le principe fondamental de la dynamique énonce que pour chaque corps i, la force gravitationnelle s'écrit :
En multipliant par ri et en sommant sur toutes les masses i, cela donne :
Avec :
,
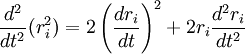et sachant que (par échange des indices muets) :
d'où :
il vient :
d'où finalement :
On reconnaît dans cette équation :
- l'énergie potentielle
- deux fois l'énergie cinétique
À l'équilibre, Ï = 0 donc
- Ep + 2Ec = 0
ce qu'il fallait démontrer.
En physique quantique
- Enoncé
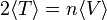
- avec
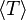correspond à la valeur moyenne de l'énergie cinétique - et
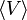correspond à la valeur moyenne du potentiel s'exprimant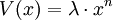 
- Démonstration
Montrons que ![\langle [H,XP] \rangle = 0](https://static.techno-science.net/illustration/Definitions/autres/e/e1206bed380f2e91a8c4c220e0228451_365b04a04aa5252442f08cdb74e239d3.png){kind=small}
:
![\langle [H,XP] \rangle = \langle \phi|HXP| \phi\rangle - \langle \phi|XPH| \phi\rangle](https://static.techno-science.net/illustration/Definitions/autres/5/5f9e36f480e09b125396f2fa79135bae_bf1266d3669e2dcab52ce15fad85ce1f.png){kind=small}
Or, 
et 
Ainsi ![\langle [H,XP] \rangle = E \langle \phi|XP| \phi\rangle - E \langle \phi|XP| \phi\rangle](https://static.techno-science.net/illustration/Definitions/autres/6/62df1c5252672a40030b3018e283e6ed_e249ec03d291440bb2ebb2f772a813cf.png){kind=small}
(1)
Travaillons sur [H,XP] :
- [H,XP] = HXP − XPH = HXP − XHP + XHP − XPH
Alors, [H,XP] = [H,X]P + X[H,P] (2)
Exprimons [H,X] et [H,P] :
![[H,X] = -[X,H] = \frac{-[X,P^2]}{2m} = \frac{-ih \cdot P}{m}](https://static.techno-science.net/illustration/Definitions/autres/a/a7f3bf17b42d5acf9eb3605ce1a333eb_014e6a33e34f315e6f1d128753db32f3.png)
![[H,P] = [V(x),P] = ih \frac{\partial V}{\partial x}](https://static.techno-science.net/illustration/Definitions/autres/0/0b41b2a80fe7fe038a00b067a8ac82ab_b8990f039d089edae23c94f6a380a5c2.png)
(3)
Revenons sur :
Alors, en utilisant (2), on trouve:
![0 = \langle [H,X]P\rangle + \langle X [H,P]\rangle](https://static.techno-science.net/illustration/Definitions/autres/c/cab463c1929c9245f6fa36f1505d68cd_2c38103de8ea32e990de6fa47bd3bba2.png){kind=small}
De même, en utilisant (3), on trouve
D'où le résultat espéré :
En thermodynamique
Applications
En astrophysique
Le théorème du viriel est très utilisé en dynamique galactique. Il permet par exemple d'obtenir rapidement un ordre de grandeur de la masse totale M d'un amas d'étoiles si l'on connaît la vitesse moyenne V des étoiles dans l'amas et la distance moyenne R entre deux étoiles de l'amas, qui peuvent être estimés à partir des observations :
- Ec ~ ½MV²
- Ep ~ - GM²/R
Il vient alors 2Ec = - Ep <=> M = RV²/G
L'énigme de la matière noire
Comme il est possible par ailleurs de déterminer la masse des étoiles visibles à partir de leur luminosité, on peut comparer la masse totale obtenue par le théorème du viriel à la masse visible. La constatation d'une différence considérable (facteur 10 à l'échelle des galaxies et facteur 100 à l'échelle des amas) entre les deux grandeurs a conduit les astrophysiciens à supposer l'existence de matière noire, c'est-à-dire non détectable par nos instruments. La seule autre explication possible serait que la loi de la gravitation n'est pas valable à grande échelle, mais aucune piste en ce sens n'a donné de résultat à ce jour.
On peut montrer que cette matière noire domine la masse des galaxies à l'extérieur du disque, dans le halo où elle s'étend jusqu'à 100-200 kiloparsecs (kpc) – contre 10-20 kpc pour la masse visible.
En thermodynamique
Ressources externes
|
|