Additionneur - Définition
Un additionneur est un circuit électronique permettant de faire une addition.
On dénote deux types d'additionneurs : parallèle et série. Dans la classe des additionneurs parallèles, nous décrirons ici ceux à propagation de retenue et ceux à retenue anticipée.
Additionneur parallèle
Codée sur un bit, la table de vérité de l'addition est :
| A | B | A + B | Retenue |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Demi-additionneur
À partir de cette table de vérité on peut par exemple construire le circuit suivant, appelé " demi-additionneur " :
Additionneur complet
Un additionneur complet nécessite une entrée supplémentaire : une retenue. L'intérêt de celle-ci est de permettre le chaînage des circuits. La table de vérité d'un additionneur complet est :
| A | B | REntrée | A + B + REntrée | RSortie |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Le circuit correspondant, l'additionneur complet, est composé de deux demi-additionneurs en série accompagnés d'une logique pour calculer la retenue (un OU entre les deux retenues générables par chacun des demi-additionneurs) :
Additionneur parallèle à propagation de retenue
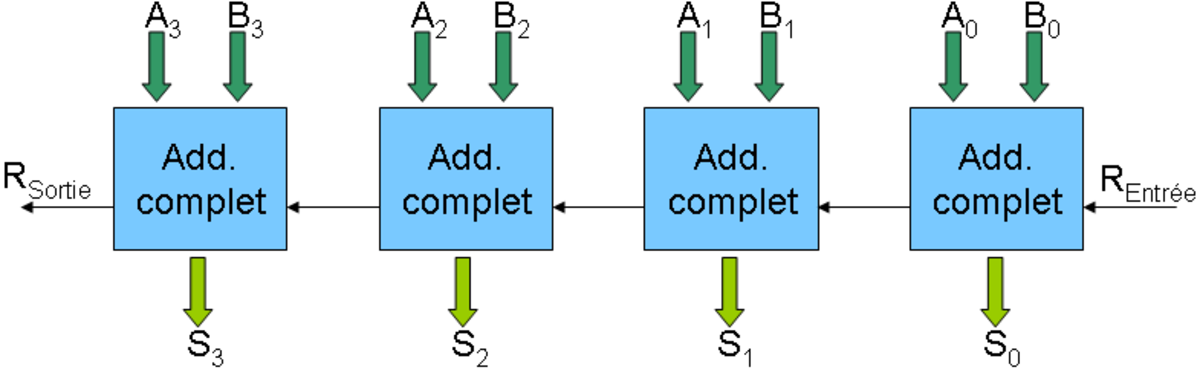
Il est possible de chaîner plusieurs additionneurs un bit pour en fabriquer un capable de traiter des mots de longueurs arbitraires :
L'inconvénient de ce circuit est sa lenteur car il dépend du temps de propagation de la retenue de module en module. Cette conception ne peut être choisie pour des circuits dépassant quelques bits, à moins de n'avoir aucune contrainte de temps.
Additionneur parallèle à retenue anticipée
Dans ce qui suit on note A et B le cumulande et le cumulateur. R est la retenue. Xindice indique le bit auquel on s'intéresse, 0 étant l'indice de poids le plus faible. La fonction logique OU est notée " + ". La fonction logique ET est notée " . " ou n'est pas notée du tout (ainsi A B est l'équivalent de A . B ou A ET B).
Tout d'abord on constate que le calcul de la retenue est tout à fait faisable théoriquement : dans la pratique il nécessite beaucoup trop de portes logiques. Pour le second additionneur, la retenue (en entrée) est égale à :
- R1 = (A0 . B0) + (A0 . R0) + (B0 . R0) (1)
Pour le troisième additionneur, la retenue est égale à :
- R2 = (A1 . B1) + (A1 . R1) + (B1 . R1) (2)
et ainsi de suite. On peut substituer R1 dans (2) par sa valeur (1). On voit immédiatement que le résultat est une formule très longue rendant cette technique totalement impraticable pour un additionneur de, par exemple, 16 bits.
Il faut donc trouver un compromis entre vitesse et complexité du circuit chargé de calculer les retenues. Cela peut se faire par l'utilisation de deux valeurs intermédiaires : la retenue propagée et la retenue générée. Nommées p et g, elles sont définies ainsi :
- p, la retenue propagée sera égale à 1 si l'un des bits du cumulande ou cumulateur est à 1 : pi = Ai OUexclusif Bi.
- g, la retenue générée sera égale à 1 si à la fois le bit en question du cumulande et du cumulateur sont à 1 : gi = Ai ET Bi.
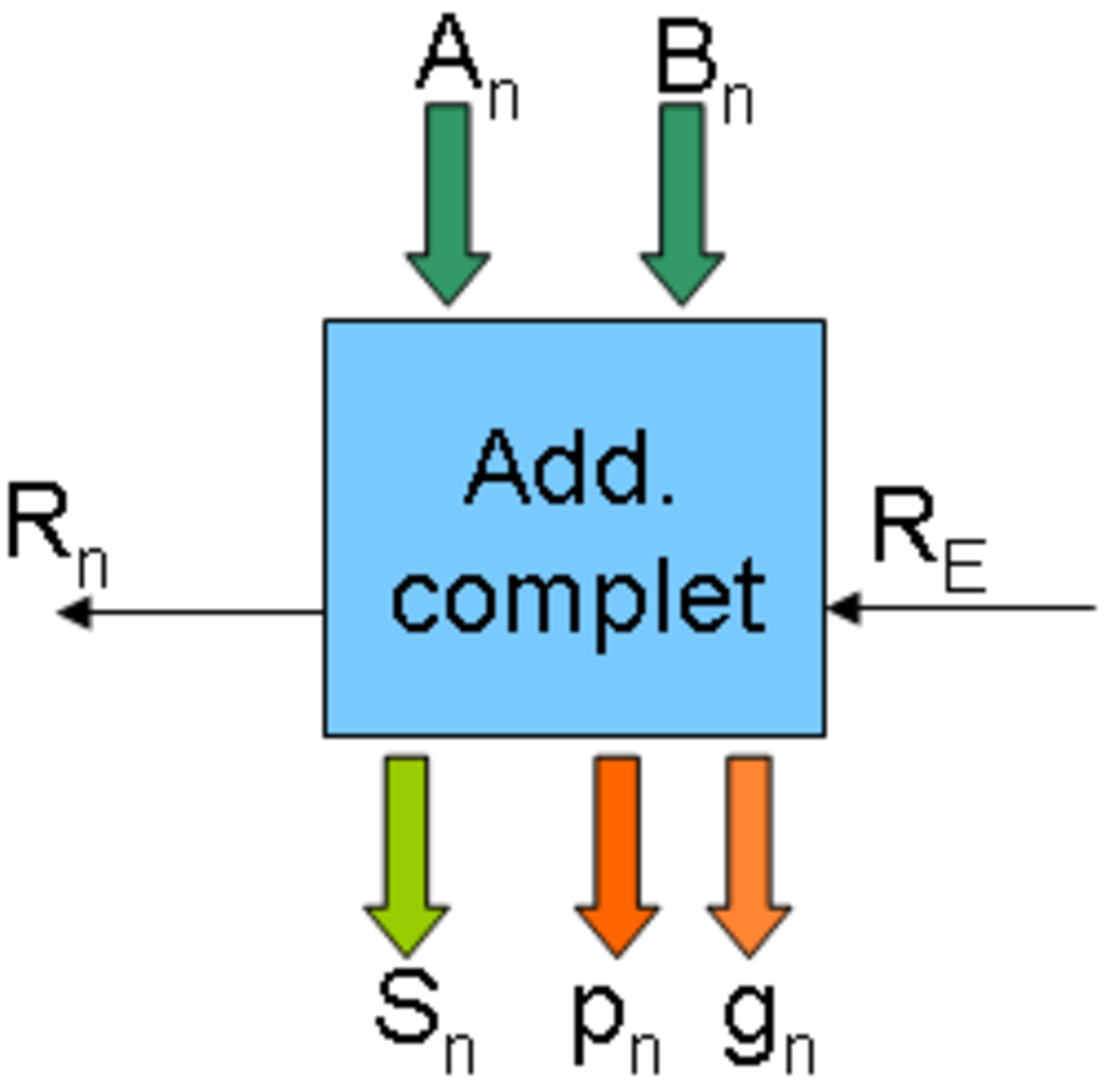
Comme en base 10, si les deux chiffres à additionner forment un résultat supérieur à 9, alors une retenue est générée, et si deux chiffres forment le total 9, alors la retenue (éventuellement issue de la colonne de chiffres précédente) sera propagée. On peut facilement modifier un additionneur complet pour en extraire ces deux nouveaux signaux.
Ensuite, on peut constater que la retenue du second additionneur peut être facilement calculée : en effet, à partir du premier additionneur et de ses sorties p et g, la retenue sera à 1 si g est à 1 (elle est générée), ou bien p est à 1 en même temps qu'on à déjà une retenue. C’est-à-dire : R1 = g0 OU (p0 ET R0), et ainsi de suite :
- R2 = g1 + (p1 . g0) + (p1 . p0 . r0)
- R3 = g2 + (p2 . g1) + (p2 . p1 . g0) + (p2 . p1 . p0 . r0)
- R4 = g3 + (p3 . g2) + (p3 . p2 . g1) + (p3 . p2 . p1 . g0) + (p3 . p2 . p1 . p0 . r0)
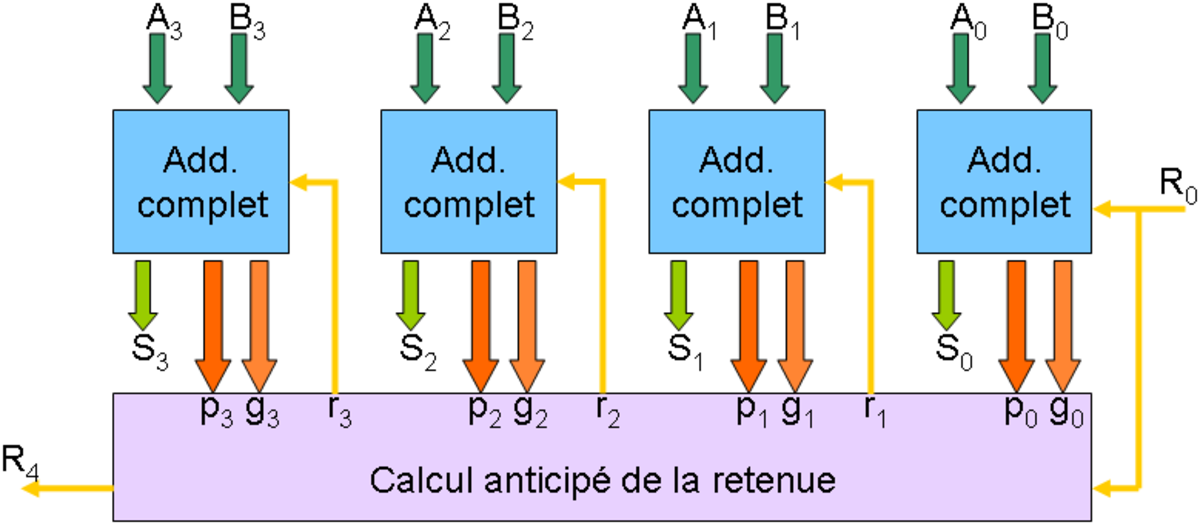
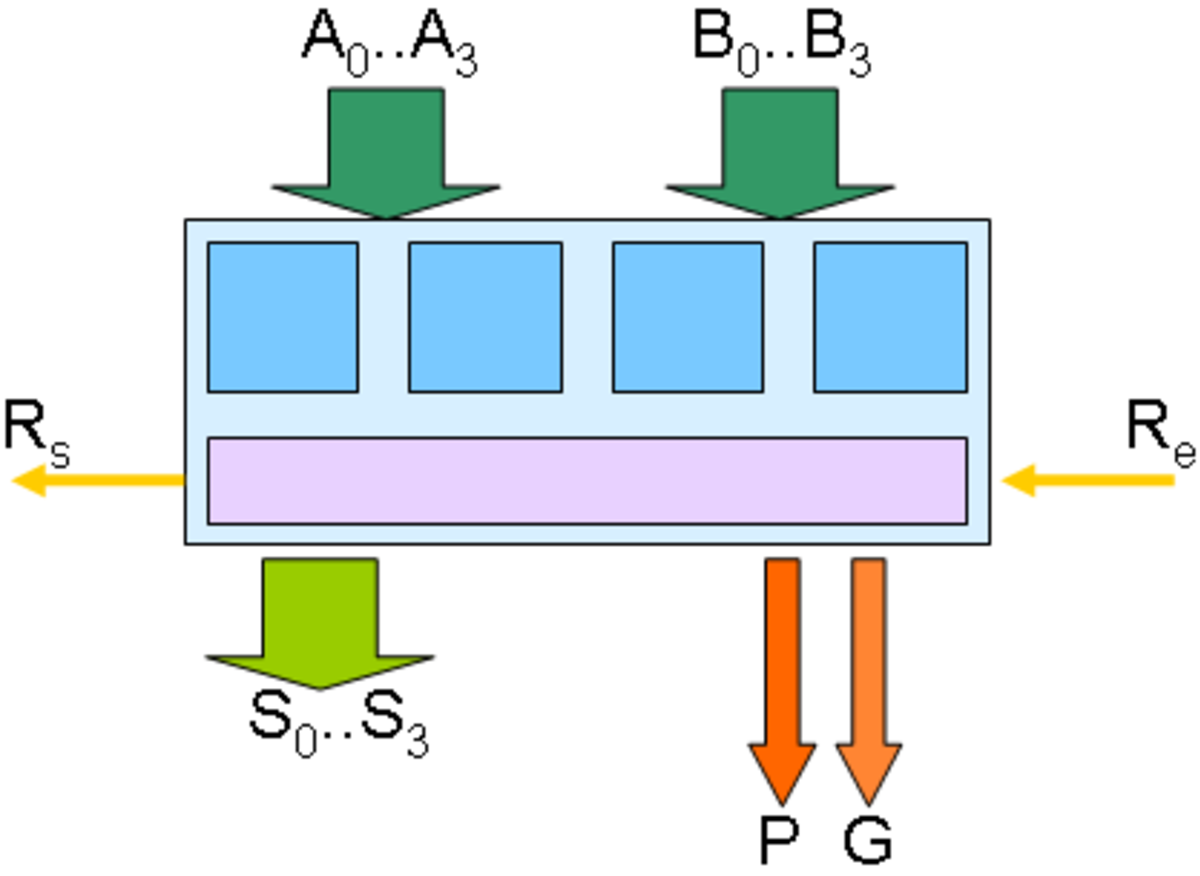
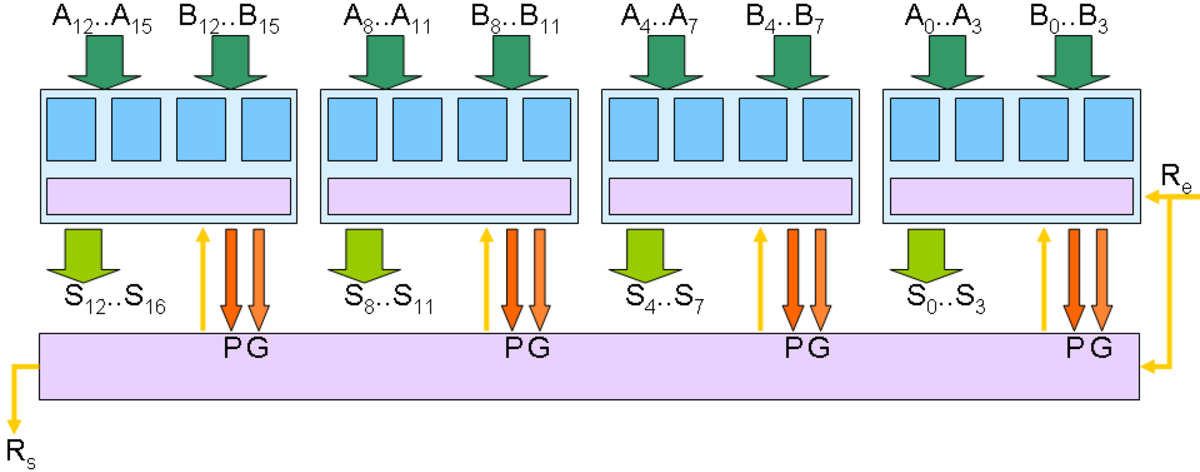
On peut étendre ce principe à des additionneurs N bits, chacun composé de N additionneurs 1 bit et son unité de calcul anticipé de la retenue. Par exemple, un bloc de base avec N = 4 peut être représenté schématiquement comme ceci :
Ces blocs sont à leur tour cascadables pour former un additionneur 16 bits :
Additionneur série
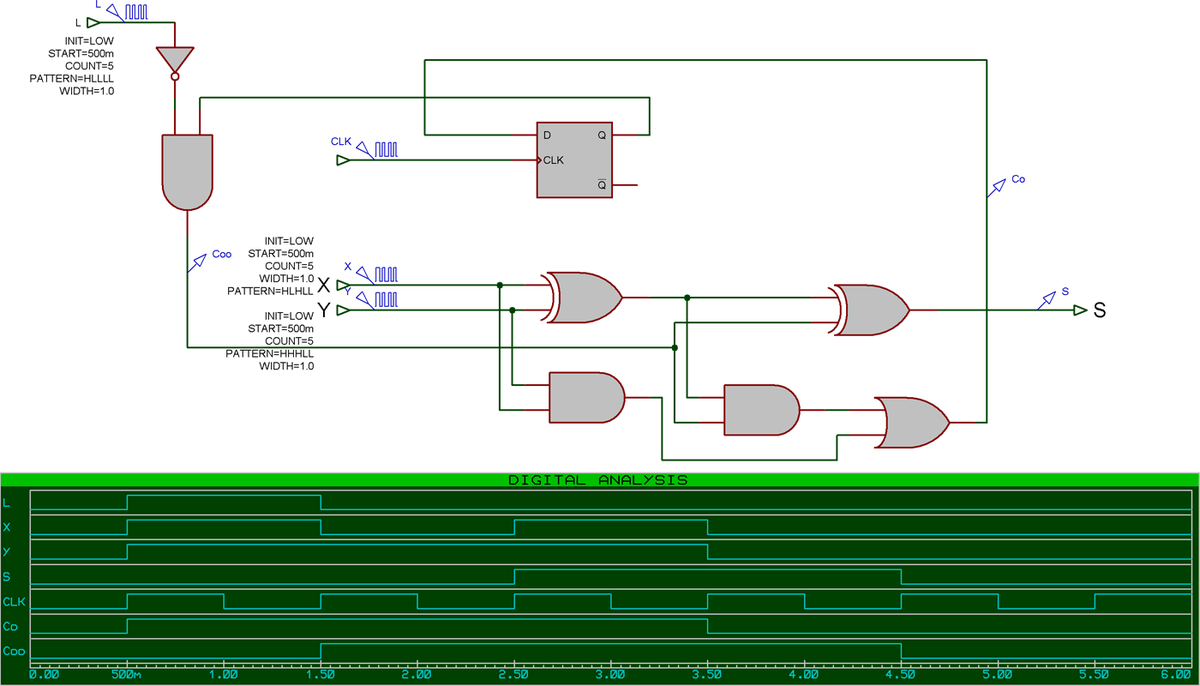
Les premiers ordinateurs utilisaient un additionneur série. Ce circuit n'est plus combinatoire mais capable de produire un bit du résultat à chaque impulsion de l'horloge qui le cadence. Un tel circuit est extrêmement simple :
Ce circuit est constitué de trois parties :
- la porte ET commandée par l'entrée L qui permet de spécifier l'arrivée du premier bit de poids faible dans le circuit ;
- une bascule de type D pour mémoriser la valeur de la retenue à l'étape précédente ;
- un additionneur complet 1 bit dont les entrées X et Y sont les nombres à ajouter et dont l'entrée Retenue est relié à la sortie de la bascule D.
Le chronogramme indique bien que 5 (X) + 7 (Y) = 12 (S) (101 + 111 = 0011 en binaire, en lisant de droite à gauche). L'état des retenues Co et Coo est indiqué de manière purement informative.
Optimisation des additionneurs
Les additionneurs sont au cœur des unités arithmétique et logique des processeurs. Des techniques très particulières sont mises en œuvre pour additionner le plus vite possible, le plus souvent en utilisant des techniques complexes de prédiction de la retenue (cf. références). Par exemple on peut détecter des blocs (série de bits consécutifs) ne générant pas de retenue, et donc très rapides à additionner. On peut aussi calculer deux résultats indépendamment et en parallèle, l'un avec une retenue, l'autre sans, et ensuite choisir le bon (via un multiplexeur).