Pendule elliptique - Définition

Soit un pendule pesant composé dont le point de suspension H est libre de glisser sur un axe horizontal sans frottement. La théorie du pendule pesant composé permet de ramener le problème à une haltère avec une masse m en H et une autre masse M en C, centre de percussion relatif à H : un tel pendule s'appelle pendule elliptique .

Il y a, a priori, deux degrés de liberté : OH = x(t) et l'élongation de C, θ(t) ; mais comme il n'y a aucune force externe horizontale, m .x(t) + M.l.sinθ(t) = 0 (l := HC) en se plaçant dans le référentiel galiléen adéquat: le barycentre G du système décrit alors la verticale selon le mouvement z= -a.cosθ(t).

Le point G décrit une verticale, le point H une horizontale, le point C fixe sur cette barre rigide décrit une portion d'ellipse (théorème dit de la bande de papier de la Hire): d'où le nom : pendule elliptique.

Petites oscillations

On sait que le problème complet du pendule simple est délicat.

Ici, ne sera traité que le problème des petites oscillations.

Le théorème du moment cinétique appliqué en H dans le référentiel R(H origine), à la masse située en C donne :

,

soit compte-tenu de la relation m.x + M.l.θ =0,

d'où la période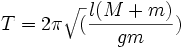 

Remarque: ce problème est usuellement résolu par la méthode des équations de Lagrange, puisqu'il n'y a pas de frottement; on retrouve bien sûr les résultats précédents.

Calcul des réactions, cas général

Si les oscillations ne sont pas petites, appliquer le théorème de l'énergie cinétique donne :

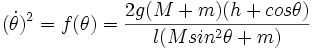
donc

On en tire aisément :

N = mg + T cosθ

avec T tension de la barre :

T = Ml.f +ml/2.g.tanθ +Mg/cosθ

Bien sûr, selon la valeur des données initiales , reflétées par la valeur de h , il y aura comme pour le pendule simple , oscillattions ou tournoiement.

La quadrature donnant θ(t)n'est clairement pas facile.