Losange - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Dans un espace affine normé, un losange, anciennement appelé rhombe, est un parallélogramme ayant deux côtés consécutifs de même longueur.
![](https://static.techno-science.net/illustration/Definitions/1200px/r/rhombus.svg_a5d68efced680f46fea19f30064684d5.png")
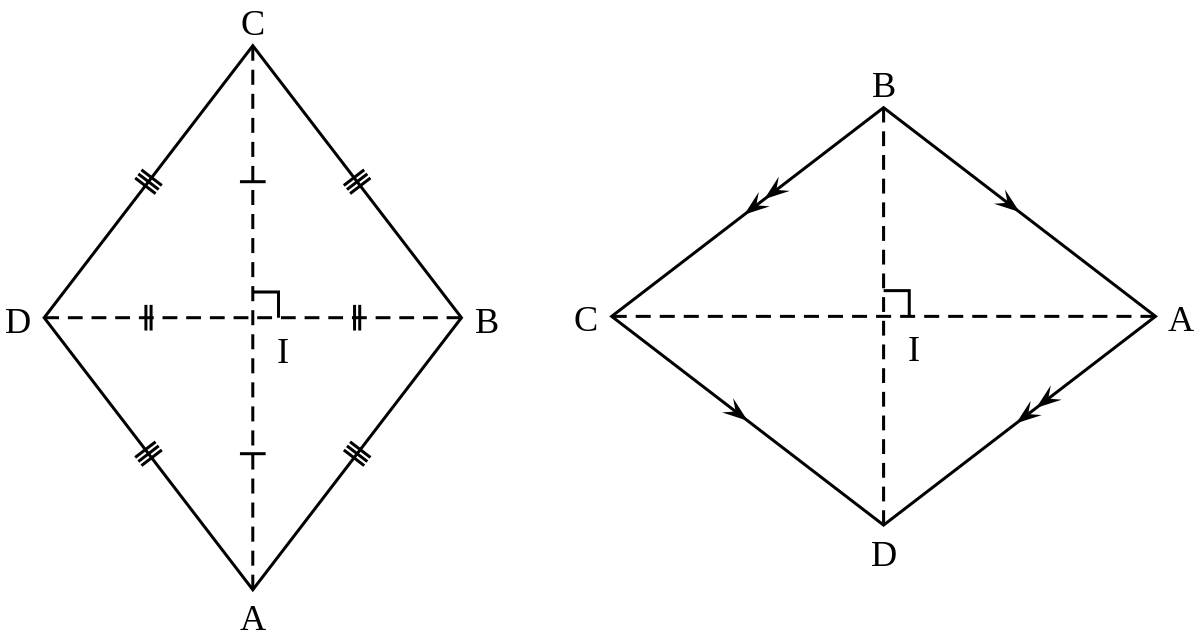
Propriétés
Propriété 1
Pour tout quadrilatère (quadrilatère est une forme geometrique qui a 4cotés) d'un plan affine euclidien (espace affine euclidien de dimension 2) les propositions suivantes sont équivalentes :
- Le quadrilatère est un losange.
- Le quadrilatère a ses quatre côtés de même longueur.
- Le quadrilatère est un parallélogramme et ses diagonales sont perpendiculaires et se coupent en leur milieu.
- Le losange est un parallélogramme ayant 2 cotés consécutifs de même longueur.
Ces équivalences sont cependant en défaut dans le cas d'un losange aplati (le point 3 n'a alors pas de sens) :
![Losange aplati ABCD](https://static.techno-science.net/illustration/Definitions/1200px/l/losangeaplati.svg_a7ed0b4758ddad552e163e387b9cef5c.png"){kind=small}
Preuve
Soit ABCD un quadrilatère. Soit I le milieu de [AC] et J le milieu de [BD].
Comme A 
C on peut parler de la médiatrice dAC de [AC]. Comme B D on peut parler de la médiatrice dBD de [BD].
Montrons (1) implique (2) :
On suppose que ABCD est un losange.
Comme c'est un parallélogramme, on a AB = CD, BC = AD et comme c'est un losange, on a AB = CB. Par transitivité, AB = BC = CD = DA.
Montrons (2) implique (3) :
On suppose que AB = BC = CD = DA.
De AB = BC et CD = DA, on conclut (DB) = dAC. Ainsi (DB) est perpendiculaire à (AC) et I appartient à (DB) et (AC).
De BC = CD, on conclut que 
.
On a 
et 
donc 
. Comme dBD et (AC) ont le point C en commun, on conclut que dBD = (AC) et donc que J appartient à (AC) et (BD).
Comme (AC) et (BD) sont perpendiculaires, elles ont un unique point commun et donc I = J. ABCD a ses diagonales qui se coupent en leur milieu, c'est donc un parallélogramme.
Montrons (3) implique (1) :
On suppose que (AC) et (BD) sont perpendiculaires et que ABCD est un parallélogramme. Comme (AC) est perpendiculaire à (BD) et passe par J, on conclut que (AC) = dBD et donc que CB = CD.
Propriété 2
Les diagonales d'un losange sont les bissectrices de ses angles.
Preuve
Soit un losange ABCD de centre O. La propriété 1 entraîne que les triangles ABO, CBO, ADO et CDO sont superposables. D'où :
= 
= 
= 
= 
= 
= 
c'est-à-dire les diagonales du losange sont les bissectrices de ses angles
Propriété 3
Les angles opposés d'un losange ont la même mesure deux à deux.
Preuve
Soit un losange ABCD de centre O. D'après la preuve de la propriété 2 :
= = =
= = =
Donc, 
= 
et 
= 
.
Propriété 4
Un losange a au moins deux axes de symétrie : ses diagonales.
Preuve
Soit un losange ABCD de centre O. D'après 3. de la propriété 1, les diagonales se coupent en leur milieu (propriété du parallélogramme) et sont perpendiculaires. Donc C est l'image de A par la symétrie d'axe (BD) et D est l'image de B par la symétrie d'axe (AC).
Propriété 5
Condition pour qu'un parallélogramme soit un losange :
- Si un parallélogramme possède 2 côtés consécutifs de même longueur alors c'est un losange.
- Si un parallélogramme a ses diagonales perpendiculaires alors c'est un losange.
Aire
où "d" représente la longueur de la petite diagonale et "D" représente la longueur de la grande diagonale du losange.
Remarque
La définition du losange comme étant un parallélogramme impose qu'un losange est une figure plane. Il existe des quadrilatères (avec quatre sommets bien distincts) ayant les quatre côtés de même longueur qui ne sont pas des losanges. Il suffit de se placer dans un espace affine euclidien de dimension 3 et de faire subir à un côté d'un "vrai losange" une rotation suivant l'une de ses diagonales.