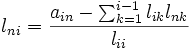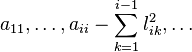Factorisation de Cholesky - Définition
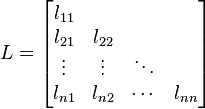
La factorisation de Cholesky, nommée d'après André-Louis Cholesky, consiste, pour une matrice symétrique définie positive A, à déterminer une matrice triangulaire inférieure L tel que : A=LLT.
La matrice L est en quelque sorte une " racine carrée " de A. Cette décomposition permet notamment de calculer la matrice inverse A-1, de calculer le déterminant de A (égal au carré du produit des éléments diagonaux de L) ou encore de simuler une loi multinormale.
Exemple
La matrice symétrique A :

est égale au produit à droite de la matrice triangulaire L :
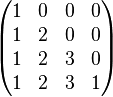
et de sa transposée LT.
Théorème
Factorisation de Cholesky d'une matrice :
Si A est une matrice symétrique définie positive, il existe au moins une matrice réelle triangulaire inférieure L telle que :
- A=LLT
On peut également imposer que les éléments diagonaux de la matrice L soient tous positifs, et la factorisation correspondante est alors unique.
Algorithme
On cherche la matrice :
De l'égalité A=LLT on déduit :
puisque lpq=0 si 1≤p La matrice A étant symétrique, il suffit que les relations ci-dessus soient vérifiées pour i≤j, c'est-à-dire que les éléments lij de la matrice L doivent satisfaire : Pour i=1, on détermine la première colonne de L : On détermine la jème colonne de L, après avoir calculé les (j-1) premières colonnes : Il résulte du théorème précédent qu'il est possible de choisir tous les éléments lii>0 en assurant que toutes les quantités sont positives.
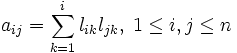
![]()
![]()
![]()
![]() d'où
d'où 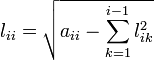
![]() d'où
d'où 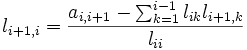
![]() d'où
d'où