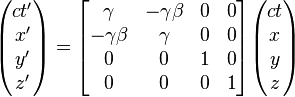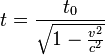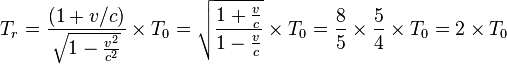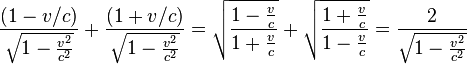Samedi 20 Avril 2024
Physique

Formulaire de relativité restreinte - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs est disponible ici.
\Delta=\nabla^2


Cet article fait partie de la série
formulaire de physique
Optique
Relativité restreinte
Physique quantique
Electrostatique
Magnétostatique
Electromagnétisme
Mécanique des fluides
Thermodynamique
Physique statistique
Analyse vectorielle
Electronique analogique
Mécanique

Les transformations de Galilée

x = (x' + vt') \qquad y = y' \qquad z = z' \qquad t = t'

les vitesses et acccélérations \vec{V} et \vec{V'}, \vec{a} et \vec{a'}(du mobile par rapport à chacun des référentiels, respectivement) :

\frac{dx}{dt} = \frac{d(x' + vt')}{dt}=\frac{d(x'+vt')}{dt'} \Rightarrow V_x=V'_x +v \frac{dy}{dt} =\frac{dy'}{dt'} \Rightarrow V_y=V'_y \qquad \frac{dz}{dt} =\frac{dz'}{dt'} \Rightarrow V_z=V'_z

et

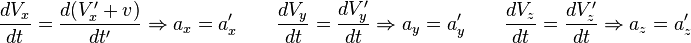\frac{dV_x}{dt} = \frac{d(V_x' + v)}{dt'} \Rightarrow a_x=a_x' \qquad \frac{dV_y}{dt} = \frac{dV_y' }{dt} \Rightarrow a_y=a_y' \qquad \frac{dV_z}{dt} = \frac{dV_z'}{dt} \Rightarrow a_z=a_z';

ce que l'on peut écrire vectoriellement :

\vec V = \vec V'+ \vec{v} \qquad , \qquad \vec{a} = \vec{a'}.
\vec{F} = m \vec{a} \qquad , \qquad \vec{F'} = m \vec{a'}.

Les transformations de Lorentz

Dans le cadre des transformations spéciales, les hypothèses d'Einstein mènent aux transformations suivantes :

Les transformations de Lorentz

x = \gamma (x' + vt') \qquad y = y' \qquad z = z' \qquad t = \gamma (t' + \frac{vx'}{c^2})
où γ est un facteur scalaire sans dimension défini par
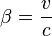
\qquad \gamma=\gamma (v)= \frac {1}{\sqrt{1-\frac{v^2}{c^2}}} et \beta=\frac{v}{c}
On a donc
\begin{pmatrix} ct\\x\\y\\z\\\end{pmatrix} = \begin{bmatrix} \gamma & +\gamma\beta& 0 & 0\\ +\gamma\beta & \gamma & 0& 0\\ 0 & 0 & 1& 0\\ 0 & 0 & 0& 1\end{bmatrix}\begin{pmatrix} ct'\\x'\\y'\\z'\\\end{pmatrix} Et inversement: \begin{pmatrix} ct'\\x'\\y'\\z'\\\end{pmatrix} = \begin{bmatrix} \gamma & -\gamma\beta& 0 & 0\\ -\gamma\beta & \gamma & 0& 0\\ 0 & 0 & 1& 0\\ 0 & 0 & 0& 1\end{bmatrix}\begin{pmatrix} ct\\x\\y\\z\\\end{pmatrix}

Ces transformations forment un groupe

La dilatation du temps

(ct'1,0,0,0) et (ct'2,0,0,0) sont les coordonnées de deux évènements qui se sont produits dans \mathbb{R'} à l'origine :

ct'_1-ct'_2=\gamma\left((ct_1-\frac{v}{c}x_1)-(ct_2-\frac{v}{c}x_2)\right) =\gamma\left(c(t_1-t_2)-\frac{v}{c}(x_1-x_2)\right) =\gamma c(t_1-t_2)(1-\frac{v^2}{c^2})

t0 = t'1 − t'2 l'intervalle de temps (dit temps propre) séparant les deux évènements dans \mathbb{R'} et t = t1 − t2 l'intervale observée dans le référentiel \mathbb{R},

t=\frac{t_0}{\sqrt{1-\frac{v^2}{c^2}}}

Autre démarche pour un même résultat: (ct'1,x',y',z') et (ct'2,x',y',z') sont les coordonnées de deux évènements qui se sont produits dans \mathbb{R'} au même point de coordonnées x',y',z', mais à des instants différents t'1,t'2

\begin{matrix} \\ ct_1-ct_2=\gamma\left((ct'_1+\frac{v}{c}x')-(ct'_2+\frac{v}{c}x')\right)=\gamma\left(ct'_1-ct'_2\right) \\ x_1-x_2=\gamma\left((x'+\frac{v}{c}t'_1)-(x'+\frac{v}{c}t'_2)\right)=\gamma\frac{v}{c}(ct'_1-ct'_2) \\ \end{matrix}

Les deux évènements sont séparés dans \mathbb{R} par un intervalle de temps γ fois plus grand que dans \mathbb{R'}: c'est la dilatation du temps.

La deuxième ligne exprime que dans \mathbb{R}:x_1-x_2= v(t_1 - t_2)

Le voyage dans le futur des autres

On considère R' le référentiel du voyageur A qui se déplace à 3/5 c ce qui donne une dilatation du temps de

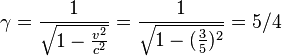
\gamma = \frac {1}{\sqrt{1-\frac{v^2}{c^2}}}=\frac {1}{\sqrt{1-(\frac{3}{5})^2}}=5/4
Si T0 est la durée du voyage dans R', dans R le voyage aller a duré T1 = γT0 = 5/4 années, en parcourant vγT0= 3/5 × 5/4 T0 année-lumière= 3/4 T0 a.l.

(a.l. signifie année lumière ou distance parcourue par la lumière en un an )

Pour simplifier prenons un voyage de T0 = 1 an et pour moderniser le voyage, O et O' sont sous vidéo avec émission en continu.
Par effet Doppler, les émissions sont reçues au ralenti avec un facteur (1+v/c) = 8/5 qui combiné avec la dilatation du temps 5/4 donne
T_r = \frac {(1+v/c)}{\sqrt{1-\frac{v^2}{c^2}}} \times T_0= \sqrt{\frac {1+\frac{v}{c}}{1-\frac{v}{c}}} \times T_0=\frac {8}{5}\times \frac{5}{4}\times T_0= 2\times T_0

Il faut donc à chacun, et la situation est symétrique pour B en O et A en O', le double de temps pour visionner en " direct " la vie de l'autre tant que ni l'un ni l'autre ne modifie son mouvement.

  • Supposons que A s'arrète au bout d'un an, sans revenir.
Point de vue de A : Il a reçu 6 mois de la vie de B au ralenti en un an de son trajet et recevra la suite de vie de B avec un retard de 3/4 d'an à un rythme normal. La dernière minute des six mois de la vie de B, visionnée au ralenti par A, a été émise 3/4 d'an plus tôt : A sait donc que B a vécu 5/4 d'année depuis son départ, ce qui est bien la durée T1 du voyage de A dans le référentiel de B.
Point de vue de B : Après avoir reçu au ralenti le voyage aller de A en 2 ans, B reçoit la vie de A avec un retard de 3/4 d'an à un rythme normal. La dernière minute du voyage de A, visionnée au ralenti par B, a été émise 3/4 d'an plus tôt : B sait donc que le voyage de A a duré (dans le référentiel de B) 2 ans moins 3/4 année, soit 5/4 d'année, ce qui est bien la durée T1 du voyage de A dans le référentiel de B.
  • Supposons maintenant que A en O' fasse demi tour au bout d'un an temps propre pour lui :
Point de vue de A : Il n'a alors visionné que 6 mois de la vie de B situé en O et il lui reste à recevoir ce qui est sur les 3/4 a.l qui séparent O de O', soit 3/4 ans du vécu de B en O non visionné par A situé en O', auquel il faudra ajouter la durée de vie de B pendant le voyage retour de A, soit T1 = 5/4 ans de la vie de B. A recevra donc en accéléré, en un an de son voyage retour, 2 ans de vie de B en O, ce qui est bien conforme à une réception en accéléré due au fait que le voyage retour rapproche A et O. En effet :
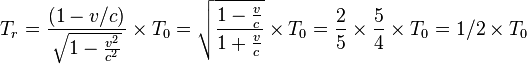
T_r = \frac {(1-v/c)}{\sqrt{1-\frac{v^2}{c^2}}} \times T_0= \sqrt{\frac {1-\frac{v}{c}}{1+\frac{v}{c}}} \times T_0=\frac {2}{5}\times \frac{5}{4}\times T_0= 1/2\times T_0
A a donc voyagé pendant 2 ans et se retrouve avec B en O qui a vécu 6 mois + 2 ans = 2 ans et demi = 2T1.
C'est l'effet dilatation du temps.
Noter que A a fait demi tour dans un espace contenant des ondes qui se propagent vers B en O.
Point de vue de B : En O, il reçoit pendant 2 ans le voyage aller de A en O' et lorsque A fait demi-tour, il ne le sait pas encore. Lorsqu'il reçoit l'information que A en O' a fait demi tour il y a déjà 3/4 d'an que A voyage sur le retour et A sera dans 6 mois en O : B en O reçoit ce retour d'un an de la vie de A en accéléré en ces 6 mois. B aura mis 2 ans et 6 mois pour recevoir les " 2ans " de voyage de A.
\frac {(1-v/c)}{\sqrt{1-\frac{v^2}{c^2}}}+ \frac {(1+v/c)}{\sqrt{1-\frac{v^2}{c^2}}}= \sqrt{\frac {1-\frac{v}{c}}{1+\frac{v}{c}}}+\sqrt{\frac {1+\frac{v}{c}}{1-\frac{v}{c}}}= \frac {2}{\sqrt{1-\frac{v^2}{c^2}}}

Pour bien percevoir l'effet relativiste, il faut voir ce que donnerait le formalisme classique.

  • En ce qui concerne les messages émis de B vers A, A les perçoit à l'aller en ralenti avec le facteur (1 − v / c), et au retour en accéléré avec le facteur (1 + v / c), sans le facteur spécifiquement relativiste de dilatation du temps 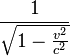\frac {1}{\sqrt{1-\frac{v^2}{c^2}}}. La longueur du trajet de A est 3cT0/5, soit 3/5 a.l. (nous gardons les mêmes unités même si elles ne sont plus vraisemblables pour faciliter la comparaison).
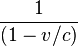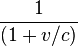  • En ce qui concerne les messages émis de A vers B, B les perçoit à l'aller de A en ralenti avec le facteur {1 \over (1-v/c)}, et au retour de A en accéléré avec le facteur {1 \over (1+v/c)}.
Point de vue de A : Pendant le voyage aller d'un an pour B, A reçoit au ralenti la vie de B avec un facteur 1 - 3/5, soit 2/5 de la vie de B. Au retour, A reçoit en accéléré la vie de B avec un facteur 1 + 3/5, soit 8/5 de la vie de B. Au cours de ses deux ans de voyage, A a visionné 2/5 + 8/5 = 2 années de la vie de B.
Point de vue de B : B reçoit au ralenti une année de voyage de A, avec un facteur 1/(1 + 3/5)) = 5/8. A cet instant, A fait demi-tour, mais B ne le sait pas encore. Il le saura lorsque le signal émis par A lui parviendra, c’est-à-dire dans 3/5 d'année. B verra donc s'écouler 1 + 3/5 = 8/5 d'années pour visionner la totalité du voyage de A avant de le voir faire demi-tour. Ces 8/5 d'années correspondent bien à un an de la vie de A visionnée au ralenti avec un facteur 5/8. Lorsque B voit A faire demi-tour, A est déjà sur le chemin du retour depuis 3/5 d'année. Il lui reste donc 2/5 d'année à voyager. B, quant à lui, visionnera en accéléré la totalité du voyage retour avec un facteur 1/(1 - 3/5)) = 5/2. Ce visionnage du retour durera donc également 2/5 d'année, et B aura visionné 8/5 + 2/5 = 2 années de voyage de A.

L'aller et le retour de A ont duré chacun 1 an, A a vécu 2 ans. Et B a vécu 2 ans pour visionner les 2 ans du voyage de A : classique quoi ! Le temps est le même pour A et B : universel.

S'inspirer des os de géants pour la construction
Il y a 9 heures
Rigidité artérielle: un nouvel indicateur pour prévenir les maladies cardiovasculaires
Il y a 9 heures
Pourquoi les femmes seules consomment-elles plus de sucreries ?
Il y a 11 heures
Que faut-il savoir sur les PFAS, ces "polluants éternels" ?
Il y a 11 heures
Découverte: ces substances courantes accélèrent le vieillissement
Il y a 1 jour
Des scientifiques identifient le meilleur moment de la journée pour faire du sport
Il y a 1 jour
Cette rupture technologique pourrait décupler la capacité des disques durs
Il y a 1 jour
Cycle menstruel: une étude scientifique établit un lien avec la Lune
Il y a 1 jour
Quand un trio d'étoiles devient un couple: une histoire cataclysmique retracée
Il y a 1 jour
Ce petit ver possède des yeux immenses: pourquoi ?
Il y a 1 jour
D'où vient cette structure fractale observée dans une bactérie ?
Il y a 2 jours
Découverte majeure dans les allergies respiratoires
Il y a 2 jours
Voici ce qui a produit la lumière la plus lumineuse jamais détectée dans l'Univers
Il y a 2 jours
Propagation inquiétante de la "mouche noire" suceuse de sang en Allemagne
Il y a 2 jours
Le hasard confère le prix Turing et 1 million de dollars au mathématicien Avi Wigderson
Il y a 2 jours
AI Act: comment encadrer l'intelligence artificielle en Europe ?
Il y a 2 jours
Quelle est cette forme étrange photographiée près de la Lune ?
Il y a 3 jours
Si vous avez déjà eu une entorse de la cheville, attention à ceci
Il y a 3 jours
Démonstration d'une nouvelle technologie de lévitation, stable et sans supraconductivité
Il y a 3 jours
Ces indices d'une rupture imminente de la faille de San Andreas
Il y a 3 jours
Cet effet inattendu de la musculation sur la mémoire
Il y a 3 jours
Les géantes Uranus et Neptune ne seraient pas faites comme nous l'imaginions
Il y a 3 jours
Parker Solar Probe se prépare à battre le record de vitesse de l'humanité
Il y a 4 jours
Nos ancêtres à l'époque des dinosaures
Il y a 4 jours
Observer directement le Big Bang avec un télescope plus puissant que le James Webb ?
Il y a 4 jours
Découverte de 17 variants génétiques liés à la maladie d'Alzheimer
Il y a 4 jours
Un immense glacier du Groenland est littéralement en train de fondre sous nos yeux
Il y a 4 jours
Découverte: des bactéries anticholestérol dans notre intestin
Il y a 4 jours
Des dinosaures aux oiseaux: cette anomalie de l'ADN a trompé les scientifiques
Il y a 5 jours
De la vie cachée 800 mètres sous terre: comment est-ce possible ?
Il y a 5 jours
Analyse d'un signal radio inhabituel, en provenance de cet objet spatial extrême
Il y a 5 jours
Ce liquide est programmable, pouvant changer de consistance et de couleur
Il y a 5 jours
Un trou noir trop léger, ou une étoile à neutrons trop lourde ? L'objet qui intrigue les scientifiques
Il y a 5 jours
Un lien démontré entre vapotage, petit-déjeuner et maux de tête
Il y a 5 jours
Un immense "arc-en-ciel" détecté sur une exoplanète
Il y a 6 jours
Des scientifiques étudient 40 ans de vie marine dans... des conserves de saumon
Il y a 6 jours
Cette innovation va améliorer significativement la sensibilité des détecteurs d'ondes gravitationnelles
Il y a 6 jours
Découverte d'une ingénierie humaine vieille de... 300 000 ans
Il y a 6 jours
Psyche: une mission à la découverte de ce très mystérieux objet spatial
Il y a 7 jours
Peur généralisée: des scientifiques découvrent comment ne pas être tétanisé par la peur
Il y a 7 jours
Découverte accidentelle d'une mémoire quantique au potentiel énorme
Il y a 7 jours
Des chercheurs ont créé artificiellement des "minifoies"
Il y a 7 jours
Surprise: la surface lunaire a "coulé" sous la croûte
Il y a 8 jours
Un curieux "point de bascule" découvert dans l'évolution des champignons
Il y a 8 jours
Des humains préhistoriques ont gravé ces traces de dinosaures
Il y a 8 jours
Ralentissement significatif d'importants courants océaniques: des répercussions graves ?
Il y a 8 jours
Les étoiles à neutrons, des aspirateurs de matière noire ?
Il y a 8 jours
Greffer de la peau de porc pour soigner les plaies
Il y a 8 jours
Le secret d'une jeunesse éternelle à proximité du trou noir de notre Voie Lactée
Il y a 9 jours
Une quantité phénoménale de volcans cachés sous l'Antarctique: des risques d'éruption ?
Il y a 9 jours
Populaires
Parker Solar Probe se prépare à battre le record de vitesse de l'humanité
Voici ce qui a produit la lumière la plus lumineuse jamais détectée dans l'Univers
S'inspirer des os de géants pour la construction
De la vie cachée 800 mètres sous terre: comment est-ce possible ?
Rigidité artérielle: un nouvel indicateur pour prévenir les maladies cardiovasculaires
Ces indices d'une rupture imminente de la faille de San Andreas
Toutes les ventes flash et Codes Promos Amazon
Cdiscount: les meilleures réductions actuelles
Page générée en 1.437 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales | Partenaire: HD-Numérique
Version anglaise | Version allemande | Version espagnole | Version portugaise