Axiomes des probabilités - Définition
Commençons par donner une définition simple d'une probabilité. Considérons une expérience aléatoire ![]() (ou épreuve aléatoire), et
(ou épreuve aléatoire), et ![]() l'univers associée à cette expérience (ensemble de tous les résultats possibles).
l'univers associée à cette expérience (ensemble de tous les résultats possibles).
Une probabilité ![]() est une application qui, à un évènement
est une application qui, à un évènement ![]() quelconque lié à l'expérience aléatoire
quelconque lié à l'expérience aléatoire ![]() , associe un nombre réel (noté
, associe un nombre réel (noté ![]() ), de telle manière que
), de telle manière que ![]() satisfasse les axiomes de Kolmogorov :
satisfasse les axiomes de Kolmogorov :
Premier axiome
Pour tout évènement ![]() :
:
C'est-à-dire que la probabilité d'un évènement est représentée par un nombre réel compris entre 0 et 1.
Deuxième axiome
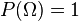 .
.
C'est-à-dire que la probabilité de l'évènement certain, ou d'obtenir un quelconque résultat de l'univers, est égale à 1. Autrement dit, la probabilité de réaliser l'un ou l'autre des évènements élémentaires est égale à 1.
Troisième axiome
Toute suite d'évènements deux à deux disjoints (on dit aussi : deux à deux incompatibles), ![]() satisfait:
satisfait:
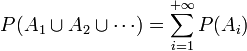 .
.
C'est-à-dire que la probabilité d'un évènement qui est la réunion (dénombrable) disjointe d'évènements est égale à la somme des probabilités de ces évènements. Ceci s'appelle la σ-additivité, ou additivité dénombrable (si les évènements ne sont pas deux à deux disjoints, cette relation n'est plus vraie en général).
Ces trois axiomes sont connus comme étant les axiomes de Kolmogorov, du nom d'Andrei Nikolaievitch Kolmogorov, mathématicien russe qui les a développés.
D'une manière plus théorique, une probabilité peut être définie comme une mesure sur une σ-algèbre ou tribu ![]() de sous-ensembles d'un univers
de sous-ensembles d'un univers ![]() (ces sous-ensembles étant les évènements), telle que la mesure de l'univers soit égale à 1.
(ces sous-ensembles étant les évènements), telle que la mesure de l'univers soit égale à 1.
Cette propriété est importante, puisqu'elle nous amène naturellement au concept de probabilité conditionnelle. Tout évènement ![]() de probabilité non nulle définit une autre probabilité
de probabilité non nulle définit une autre probabilité ![]() sur l'univers :
sur l'univers :
pour tout évènement ![]() de
de ![]() , on pose :
, on pose : 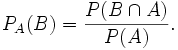
Le réel ![]() se note aussi
se note aussi ![]() et habituellement
et habituellement ![]() se lit " la probabilité conditionnelle de
se lit " la probabilité conditionnelle de ![]() , sachant
, sachant ![]() " ou " la probabilité de
" ou " la probabilité de ![]() , sachant que
, sachant que ![]() s'est réalisé ".
s'est réalisé ".
Propriétés d'une probabilité
À partir des axiomes, se démontrent un certain nombre de propriétés utiles pour le calcul des probabilités, par exemple :
-
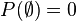 .
.
-
- si
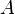 ,
, 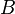 sont deux évènements incompatibles, alors
sont deux évènements incompatibles, alors 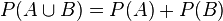 .
.
- si
-
- pour tous évènements
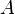 ,
, 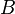 ,
, 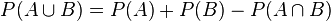 .
.
- pour tous évènements
- Ceci signifie que la probabilité pour que l'un au moins des évènements
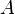 ou
ou 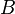 se réalise est égale à la somme des probabilités pour que
se réalise est égale à la somme des probabilités pour que 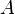 se réalise, et pour que
se réalise, et pour que 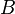 se réalise, moins la probabilité pour que
se réalise, moins la probabilité pour que 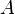 et
et 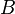 se réalisent simultanément.
se réalisent simultanément.
-
- pour tout évènement
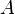 ,
, 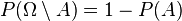 .
.
- pour tout évènement
- Ceci signifie que la probabilité pour qu'un évènement ne se produise pas est égale à 1 moins la probabilité pour qu'il se réalise ;
- cette propriété s'utilise lorsqu'il est plus simple de déterminer la probabilité de l'évènement contraire que celle de l'évènement.
-
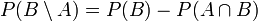 ; en particulier, si
; en particulier, si 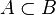 , alors
, alors 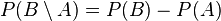
- (il en résulte que si
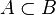 , alors
, alors 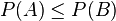 : c'est la propriété de croissance de la probabilité).
: c'est la propriété de croissance de la probabilité). - La relation précédente signifie que la probabilité que B se réalise, mais pas A, est égale à la différence
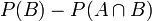 .
.