Inéquation du second degré - Définition

Cet article fait partie de la série Mathématiques élémentaires

Algèbre

Analyse

Arithmétique

Géométrie

Logique

Probabilité

Statistique

Une inéquation du second degré est une inéquation qui peut, à l'aide d'opérations élémentaires, se mettre sous la forme où a est un réel non nul

Résolution

Pour résoudre une telle inéquation, il faut étudier le signe de ax² + bx + c.

Il faut commencer par déterminer les racines réelles de ax² + bx + c. Les racines réelles sont les solutions réelles de l'équation du second degré ax² + bx + c = 0. On distingue trois cas de figure

• aucune racine
• une racine double (-b/2a)
• deux racines (x1 et x2).

L'étude du signe peut se faire par factorisation de l'expression du second degré et tableau de signe.

Ou bien, on peut utiliser les observations graphiques suivantes :

Position d'une parabole par rapport à l'axe des x pour a > 0, selon le nombre de racines.

Position d'une parabole par rapport à l'axe des x pour a < 0, selon le nombre de racines.

De ces observations, on peut tirer la règle suivante :

le polynôme ax² + bx + c est du signe de a sauf entre les racines.

Exemples

• x² − 2x + 5 a pour discriminant - 16, il ne possède pas de racine. le coefficient devant x² est 1, il est positif. Donc x² − 2x + 5 est toujours positif.
• 50 − 2x² possède deux racines 5 et - 5. Le coefficient devant x² est - 2, il est négatif donc 50 − 2x² est négatif sauf entre - 5 et 5. On peut alors résumer l'étude de signe dans un tableau de signes.

valeurs de x	- 5 + 5
signe de 50 - 2x²	- 0 + 0 -

Exemples d'inéquations

• 1) Pour un périmètre de 12 cm, quelles sont les dimensions du rectangle tel que l'aire soit supérieure à 5 cm² ?

On appelle x, une des dimensions du rectangle. Puisque le demi-périmètre est 6 cm alors l'autre dimension est 6 - x. L'aire du rectangle est donc x(6 - x). le problème revient à résoudre, dans l'intervalle [0 ; 6], l'inéquation x(6 − x) > 5. cette inéquation est successivement équivalent à

− x² + 6x > 5 on a développé et ordonné le premier membre

− x² + 6x − 5 > 0 on a retranché 5 à chaque membre de l'inégalité

Le polynôme − x² + 6x − 5 possède deux racines (discriminant = 16, racines = 1 et 5. Le coefficient devant x est -1, il est négatif donc le polynôme est négatif sauf entre 1 et 5. On souhaite que le polynôme soit strictement positif, il faut donc prendre x dans l'intervalle ]1 ; 5[

• 2) Résoudre, dans ]0 ; 6[, l'inéquation .

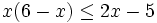L'inéquation est équivalente à 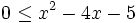. Ce polynôme possède deux racines -1 et 5. Le coeficient devant x² est positif. Le polynôme est positif sauf entre - 1 et 5. L'ensemble des solutions est donc l'intervalle [5 ; 6[.

• 3) Résoudre, dans R, l'inéquation 2x² + 25 > 0

Le polynôme 2x² + 25 ne possède pas de racine, son coefficient devant x² est 2, il est positif. Le polynôme est donc toujours strictement positif quelle que soit la valeur de x. L'ensemble des solutions est donc R.

• 4) Résoudre, dans R, l'inéquation .

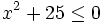Le polynôme n'admet pas de racine, le coefficient devant x² est positif, le polynôme est donc toujours positif, il n'est jamais négatif. L'ensemble des solutions est vide.

• 5) Résoudre, dans R, l'inéquation (x + 5)² > 0 .

Le polynôme admet une racine double (- 5). Le coefficient devant x² est positif, donc le polynôme est positif sauf en - 5 où il s'annule. L'ensemble des solutions est donc