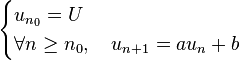Suite arithmético-géométrique - Définition
Une suite arithmético-géométrique est une suite à valeurs dans un corps et définie par récurrence par
En règle générale, on travaille sur ![]() (corps des réels) ou
(corps des réels) ou ![]() (corps des complexes).
(corps des complexes).
Utilisation
La suite arihmético-géométrique se rencontre dans la modélisation de certains flux de population (apport fixe et fuite proportionnelle ): apport de 10 et fuite de 5%, ![]()
Elle se rencontre aussi dans les plans de remboursement : un capital C emprunté à un taux mensuel t et remboursé par mensualités M conduit à l'élaboration d'un plan de remboursement . Si Rn représente le capital restant dû au bout de n mensualités, la suite ![]() est une suite arithmético-géométrique de relation de récurrence : Rn + 1 = (1 + t)Rn − M
est une suite arithmético-géométrique de relation de récurrence : Rn + 1 = (1 + t)Rn − M
On la trouve aussi dans une chaîne de Markov à deux états . La matrice stochastique est alors
De la relation
On déduit que:
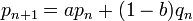 .
.
Comme d'autre part,
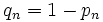 ,
,
en remplaçant on obtient
Terme général
Pour le cas trivial où a = 1, on a affaire à une suite arithmétique.
Dans le cas où ![]() , on cherche par translation à se ramener à une suite géométrique :
, on cherche par translation à se ramener à une suite géométrique :
- On pose vn = un + c
- On démontre que
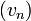 est géométrique ssi
est géométrique ssi 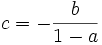
- On trouve alors que
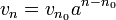
- Puis, grâce aux relations entre un et vn,
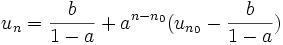
On peut aussi retrouver le terme général, en observant que cette suite consiste à construire la somme des terme d'une suite géométrique. Pour l'illustrer, on peut s'intéresser au cas de la suite définie de la manière suivante (définition 2):
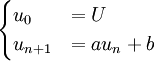 ,
,
- On remarque alors que
- u1 = aU + b
- u2 = a2U + ab + b
- u3 = a3U + a2b + ab + b
- Le terme général s'exprime par
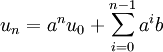 .
.
- Avec la somme des premiers termes d'une suite géométrique, on obtient le terme général suivant:
- En posant
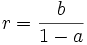 , on trouve
, on trouve
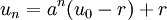 .
.
Somme des n premiers termes
Pour une suite définie suivant la définition 2, on a  .
.
Convergence
Le terme général et les considérations sur les suites géométriques permettent de déterminer la limite d'une telle suite suivant les valeurs de a et, éventuellement, le signe de ![]() .
.
Une remarque intéressante est à faire dans le cas où |a| < 1. Dans ce cas, la limite de la suite est ![]() quelle que soit la valeur initiale. La limite d'une suite de ce type est donc complètement indépendante des conditions initiales. Cette particularité est à mettre en regard avec les suites à récurrence non linéaire (fonction logistique) qui peuvent, elles, être très sensibles aux conditions initiales. Dans une chaîne de Markov, cela prouve que la chaîne converge vers une chaîne stationnaire.
quelle que soit la valeur initiale. La limite d'une suite de ce type est donc complètement indépendante des conditions initiales. Cette particularité est à mettre en regard avec les suites à récurrence non linéaire (fonction logistique) qui peuvent, elles, être très sensibles aux conditions initiales. Dans une chaîne de Markov, cela prouve que la chaîne converge vers une chaîne stationnaire.