Onde de Bloch - Définition
Dans le cadre du cristal parfait infini, les électrons sont soumis à un potentiel périodique ayant la symétrie de translation des atomes constituant le cristal. Les ondes de Bloch (d'après Felix Bloch) sont des fonctions d'ondes décrivant des états quantiques électroniques ayant la même symétrie que le cristal.
Le théorème de Bloch
On considère un cristal parfait infini. Les potentiels possèdent donc la périodicité du réseau cristallin. Examinons les états propres d'énergie d'un électron dans ce réseau.
Si nous baptisons par 
~" /> les états propres du hamiltonien et 
~" /> les états propres de chaque potentiel localisé au nœud Rn du réseau, alors nous avons 
=E |\Psi_J>~" />. Soit 
l'opérateur de translation de R. Si R appartient au réseau, alors H et commutent et ont donc les mêmes sous-espaces propres.
En utilisant la propriétés d'invariance de la norme des états propres par translation d'une période entière du réseau cristallin et la propriété de combinaison des translations, on obtient les valeurs propres de , R fixé, sous la forme 
.
On en déduit que la forme générale de la fonction d'onde dans le cas d'un cristal est 
=\Psi_{k,n}(r)=e^{ikr} u_{k,n}(r) ~" /> où 
est périodique avec la période du réseau cristallin.
=\Psi_{k,n}(r)~" /> est appelé onde de Bloch
Conséquences du théorème de Bloch
Le théorème de Bloch introduit un vecteur d'onde k. Il est nommé pseudo-moment de l'électron. Cette quantité remplace le moment 
de l'électron lorsqu'on passe du problème d'un électron se mouvant dans un milieu continu à celui d'un électron se mouvant dans un potentiel périodique. Ce pseudo-moment n'est pas proportionnel à P. En effet la dérivation 
introduit un terme supplémentaire 
. Ainsi 
n'est pas un état propre de l'opérateur quantité de mouvement. D'une façon plus générale, la non-conservation de la quantité de mouvement et la non pertinence de cette grandeur dans le cadre d'un potentiel periodique d'etendue spatiale infinie peut sembler surprenante. Il faut se rapporter au théorème de Noether pour en comprendre l'origine. En effet le théorème de Noether fait découler directement la conservation de la quantité de mouvement de la symetrie de l'espace en regard des translations infinitésimales. Or en introduisant un potentiel cristallin, on tombe dans le cas d'une symétrie brisée (translations discrètes au regard des translations infinitésimales) et l'invariant associé n'a plus de raison d'être conservé.
Les zones de Brillouin
En se plaçant dans l'espace réciproque, c'est-à-dire l'espace des k, on vérifie qu'on peut décrire l'énergie d'un état de Bloch en fonction de son vecteur k. On remarque tout de suite que k est défini à un vecteur du réseau réciproque près, à cause de la périodicité du facteur 
dans le réseau direct. Conventionnellement, on choisit k plus proche du nœud 0 du réseau réciproque que de tout autre nœud. Ce domaine est la première zone de Brillouin. La deuxième zone de Brillouin est composée des points du réseau réciproque plus proches des premiers nœuds que du nœud 0 et des deuxièmes nœuds par ordre de distance au nœud 0, et ainsi de suite. Ainsi pour décrire complètement les états d'un électron, on peut se contenter de faire varier le pseudo_moment k dans la première zone de Brillouin, à condition d'admettre que l'énergie est une fonction multiforme du moment. Les branches de la fonction énergie du vecteur k auxquelles on peut restreindre l'énergie pour avoir une fonction univoque de k sont appelées les bandes d'énergie. Les intervalles d'énergie pour lesquels il n'existe aucune branche ni aucune valeur de k correspondante sont appelés les bandes interdites.
Les bandes interdites
Apparition des bandes interdites
La tradition pédagogique des cours de physique des solides est de faire apparaître la structure des bandes interdites par l'application d'un potentiel cristallin perturbatif (donc arbitrairement faible) sur des électrons libres: c'est le modèle des électrons presque libres. Partons d'une fonction d'onde d'électron libre 
~" />
prenons le potentiel cristallin sous la forme:
Constatons d'abord que la perturbation introduite par ce potentiel ne peux pas être dans le cas général général une perturbation du premier ordre. En effet, tous les termes de ce potentiel sont oscillatoires et leur moyenne par toute fonction d'onde K sur un domaine suffisamment grand est nulle, sauf si les termes oscillatoires se compensent. On montre facilement que la fonction d'onde prend la forme:
=|k>+ \sum_{m \neq 0}u(K_m)|k+K_m>~" />avec:
![u(K_m)={{2m.V(K_m)}\over{{\hbar^2}[E(k)-(k+K_m)^2]}}~](https://static.techno-science.net/illustration/Definitions/autres/c/cf15af74d39212ef1bd99682e8d7b025_fb3165216fbe9a88a2aee723892514a0.png)
Remarquons au passage que cette fonction d'onde est bien une onde de Bloch (il suffit de remplacer les kets par leurs formes fonctionnelles). En posant E(k) = k2 et vu la nature périodique du potentiel perturbateur V, toutes ces contributions sont nulles à l'exception de celles remplissant les conditions de Bragg, c.a.d. 
ce qui donne comme valeur de E:
![E={{\hbar^2k^2}\over{2m}}\pm[V(K_p)]~](https://static.techno-science.net/illustration/Definitions/autres/0/0b438c7f6ea4ec16b35e385fa07d2336_7e9491e2800ed2203e501995a9509563.png){kind=small}
Donc pour un point k à mi distance de l'origine et d'un premier nœud du réseau réciproque, c’est-à-dire 
on a bien évidemment la condition de Bragg vérifiée et la valeur de E modifiée. Ce point est évidemment sur la frontière de la première zone de Brillouin.
Forme des fonctions d'onde au voisinage de la frontière de zone
Au voisinage de points 
,les formules données plus haut divergent, ce qui prouve que l'approche perturbative n'est pas appropriée. En fait la solution est une recombinaison de l'onde de vecteur 
et de l'onde de vecteur 
. Le couplage de ces deux niveaux provoque un éclatement de la bande d'énergies au voisinage des points et 
. Il en résulte l'ouverture autour des points d'énegie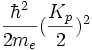 
d'un intervalle d'energie qui ne peut être atteint pour aucune valeur de k. En effet les énergies au voisinage de sont fortement éclatées et ne peuvent donc pas être solution de valeurs au voisinage immédiat de 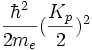. Quant aux valeurs plus distantes de k, la perturbation de l'energie est trop faible pour la ramener à proximité de la valeur .
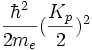Bibliographie
- Charles Kittel, Solid State Physics, Wiley (1995). ISBN 0471111813
- Ashcroft et Mermin, Physique des solides, Brooks Cole (2003, version française du livre paru en 1976). ISBN 2868835775
- O. Madelung, Introduction to Solid State Physics, Springer, 1981. ISBN 0-387-08516-5
- Blokhintsev, Mécanique quantique et applications à l'étude de la structure de la matière, Dunod, 1967. ISBN 2225509204
- Blokhintsev, Physique du solide