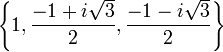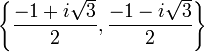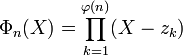Racine de l'unité - Définition
En mathématiques, étant donné un nombre entier naturel non nul n, une racine n-ième de l'unité (parfois appelée nombre de de Moivre du nom d'Abraham de Moivre) est un nombre complexe dont la puissance n-ième vaut 1. Pour un entier n donné, toutes les racines n-ième de l'unité sont situées sur le cercle unité et sont les sommets d'un polygone régulier à n côtés ayant un sommet d'affixe 1.
L'expression " racine n-ième " n'a pas valeur de norme, elle provient de l'habitude qu'ont les mathématiciens, souvent, de nommer un entier naturel n. Si l'entier en question est noté p, on parlera de " racine p-ième ", etc.
Définition
Pour un entier naturel non nul n donné, on appelle racine n-ième de l'unité toute solution complexe de l'équation
d'inconnue z. Il existe exactement n racines n-ièmes de l'unité. Les racines n-ièmes de l'unité forment un groupe cyclique d'ordre n pour la multiplication des nombres complexes avec 1 comme élément neutre.
Chaque racine du groupe a pour ordre l'entier d défini comme le plus petit entier strictement positif tel que ![]() . L'ordre d de la racine est un diviseur de n. Une racine n-ième de l'unité est dite primitive quand elle est d'ordre exactement n, c'est-à-dire quand c'est un générateur de ce groupe cyclique.
. L'ordre d de la racine est un diviseur de n. Une racine n-ième de l'unité est dite primitive quand elle est d'ordre exactement n, c'est-à-dire quand c'est un générateur de ce groupe cyclique.
Exemples
Les racines troisièmes (ou cubiques) de l'unité sont
Les racines primitives troisièmes de l'unité sont
La première est habituellement notée j et la seconde, son conjugué, ![]() .
.
Les racines quatrièmes de l'unité sont
Les racines primitives quatrièmes de l'unité sont
Propriétés
Expression complexe
Le racines n-ièmes de l'unité peuvent s'écrire sous la forme
Lorsque l'entier n est supérieur ou égal à 2, la somme de ces nombres est égale à 0, un fait simple qui est souvent utile en mathématiques. Il peut être démontré de différentes manières, par exemple en reconnaissant une somme d'une progression géométrique.
Les racines primitives n-ièmes de l'unité sont exactement les nombres de la forme ![]() où k et n sont premiers entre eux. Par conséquent, il y a
où k et n sont premiers entre eux. Par conséquent, il y a ![]() racines primitives n-ièmes de l'unité différentes, où
racines primitives n-ièmes de l'unité différentes, où ![]() désigne la fonction φ d'Euler.
désigne la fonction φ d'Euler.
Polygones réguliers
Dans le plan complexe, les points dont les affixes sont les racines n-ièmes de l'unité sont les sommets du polygone régulier à n côtés inscrit dans le cerlce de centre O (le point d'affixe zéro) et de rayon 1.
L'étude de ces nombres, grâce aux puissants outils de l'algèbre, facilite donc celle, beaucoup plus ancienne, des polygones réguliers.
Polynôme cyclotomique
Article détaillé: Polynôme cyclotomique
Les racines n-ièmes de l'unité sont précisément les racines du polynôme ![]() . Les racines primitives n-ièmes de l'unité sont exactement les racines du polynôme d'indice n suivant :
. Les racines primitives n-ièmes de l'unité sont exactement les racines du polynôme d'indice n suivant :
où ![]() sont les racines primitives n-ièmes de l'unité et
sont les racines primitives n-ièmes de l'unité et ![]() la fonction indicatrice d'Euler. Le polynôme
la fonction indicatrice d'Euler. Le polynôme ![]() a des coefficients entiers et est irréductible sur l'ensemble des rationnels (c’est-à-dire qu'il ne peut pas être écrit comme produit de deux polynômes de degré strictement positif à coefficients rationnels). Le cas particulier où n est premier, plus simple que le cas général, se déduit du critère d'Eisenstein (effectuer le changement de variable X = T+1, alors
a des coefficients entiers et est irréductible sur l'ensemble des rationnels (c’est-à-dire qu'il ne peut pas être écrit comme produit de deux polynômes de degré strictement positif à coefficients rationnels). Le cas particulier où n est premier, plus simple que le cas général, se déduit du critère d'Eisenstein (effectuer le changement de variable X = T+1, alors ![]() se traite immédiatement par le critère d'Eisenstein).
se traite immédiatement par le critère d'Eisenstein).
Chaque racine n-ième de l'unité est une racine primitive d-ième de l'unité pour exactement un diviseur positif de n. Cela implique que
Cette formule représente la décomposition du polynôme ![]() en produits de facteurs irréductibles et peut également être employée pour calculer récursivement les polynômes cyclotomiques. Par ailleurs elle permet récursivement de prouver que les polynômes cyclotomiques sont à coefficients entiers et unitaires (la division de
en produits de facteurs irréductibles et peut également être employée pour calculer récursivement les polynômes cyclotomiques. Par ailleurs elle permet récursivement de prouver que les polynômes cyclotomiques sont à coefficients entiers et unitaires (la division de ![]() par un polynôme à coef. entiers et unitaire donne bien un quotient également à coefficients entiers et unitaire.
par un polynôme à coef. entiers et unitaire donne bien un quotient également à coefficients entiers et unitaire.
Corps cyclotomiques
Article détaillé: Polynôme cyclotomique
En adjoignant une racine primitive n-ième de l'unité à ![]() , nous obtenons le corps n-cyclotomique
, nous obtenons le corps n-cyclotomique ![]() . Ce corps contient toutes les racines n-ièmes de l'unité et est le corps de décomposition sur
. Ce corps contient toutes les racines n-ièmes de l'unité et est le corps de décomposition sur ![]() du polynôme cyclotomique d'indice n. L'extension de corps
du polynôme cyclotomique d'indice n. L'extension de corps ![]() est de degré
est de degré ![]() et son groupe de Galois est naturellement isomorphe au groupe multiplicatif des inversibles de l'anneau
et son groupe de Galois est naturellement isomorphe au groupe multiplicatif des inversibles de l'anneau ![]() .
.
Comme le groupe de Galois de ![]() est abélien, c'est une extension abélienne. Tout sous-corps d'un corps cyclotomique est une extension abélienne du corps des nombres rationnels. Dans ces cas, la théorie de Galois peut être écrite tout à fait explicitement en termes de périodes gaussiennes : cette théorie tirée du Disquisitiones Arithmeticae de Gauss fut publiée beaucoup d'années avant la théorie de Galois.
est abélien, c'est une extension abélienne. Tout sous-corps d'un corps cyclotomique est une extension abélienne du corps des nombres rationnels. Dans ces cas, la théorie de Galois peut être écrite tout à fait explicitement en termes de périodes gaussiennes : cette théorie tirée du Disquisitiones Arithmeticae de Gauss fut publiée beaucoup d'années avant la théorie de Galois.
Réciproquement, chaque extension abélienne du corps des nombres rationnels est un sous-corps d'un corps cyclotomique - un théorème de Kronecker, habituellement appelé le théorème de Kronecker-Weber parce que Weber en a établi la démonstration.