Théorème des gendarmes - Définition
En analyse, le théorème des gendarmes, également appelé théorème d'encadrement ou théorème du sandwich, s'énonce de la manière suivante :
Si f, g et h sont trois fonctions réelles définies sur un même intervalle I, telles que pour tout x de I dans un voisinage de a :
![]() et
et ![]() (a fini ou non), alors on a aussi :
(a fini ou non), alors on a aussi : ![]()
Origine du nom
Pour comprendre ce nom, il faut assimiler les fonctions f et h à des gendarmes et g au prisonnier. Ce dernier, étant encadré par les deux gendarmes il est alors obligé de les suivre jusqu'à la prison L.
Démonstration
La démonstration est directement issue de la notion de voisinage de a et de la définition de la limite.
Pour tout intervalle ouvert U contenant L,
- Puisque
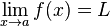 , il existe un voisinage V1 de a tel que
, il existe un voisinage V1 de a tel que
-
- pour tout x de V1,
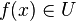
- pour tout x de V1,
- Puisque
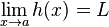 , il existe un voisinage V2 de a tel que
, il existe un voisinage V2 de a tel que
-
- pour tout x de V2,
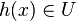
- pour tout x de V2,
- Enfin, d'après la propriété d'encadrement, il existe un voisinage V3 de a tel que
-
- pour tout x de V3,
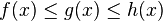
- pour tout x de V3,
L'intersection de trois voisinages est un voisinage donc ![]() est un voisinage de a et pour tout x de V, on a
est un voisinage de a et pour tout x de V, on a
d'où il vient que
ce qui prouve que ![]()
Exemple
Soit ![]() , x > 0. On cherche la limite en l'infini de cette fonction.
, x > 0. On cherche la limite en l'infini de cette fonction.
On sait que : ![]() . D'où, pour x > 0 :
. D'où, pour x > 0 : ![]()
Ou ![]()
Donc, d'après le théorème d'encadrement : ![]()
Variantes
Des variantes de ce théorème existent pour des fonctions dont la limite est infinie, mais c'est un théorème de comparaison qui n'est pas celui des gendarmes (à noter "par théorème de comparaison" donc)
- Si f, g sont deux fonctions réelles définies sur un même intervalle I, telles que pour tout x de I dans un voisinage de a :
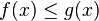 et
et 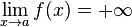 (a fini ou non), alors on a aussi :
(a fini ou non), alors on a aussi : 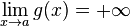
- Si f, g sont deux fonctions réelles définies sur un même intervalle I, telles que pour tout x de I dans un voisinage de a :
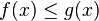 et
et  (a fini ou non), alors on a aussi :
(a fini ou non), alors on a aussi : 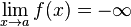
- Si f, g sont deux fonctions réelles définies sur un même intervalle I, telles que pour tout x de I dans un voisinage de a :
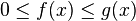 et
et 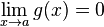 (a fini ou non), alors on a aussi :
(a fini ou non), alors on a aussi : 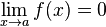
Enfin des théorèmes analogues existent pour des limites de suites
- Si u, v et w sont trois suites réelles, telles que pour tout n > N
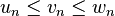 et
et 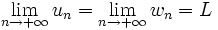 , alors on a aussi :
, alors on a aussi : 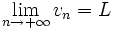
- avec les variantes pour les limites infinies.
Les démonstrations de toutes ces variantes sont analogues à celle développée plus haut.