Un petit calcul de relativité
Modérateur : Modérateurs
Un petit calcul de relativité
Je voudrais faire une comparaison entre les jumeaux de Langevin et les particules instables qui ont une durée de vie plus longues à des vitesses relativistes, dans tout les cas le temps qui me sers de référence est le temps terrestre au repos, donc admettons qu'un des jumeaux de Langevin se rends sur Alpha du centaure située à 4,3 AL à une vitesse relativiste de 2/3 de C la contraction relativiste c'est donc (1-4/9)1/2 doit racine de 5/9= Gamma= 0.745 bon pour le jumeau qui voyage son temps se dilate de cette quantité mais la distance parcourue se contracte, ce qui revient à dire qu'il ne parcourt pas 4.3 année lumière jusqu'à alpha du centaure mais 4.3 X 0.745 soient environ 3 Al... Est ce que j'ai juste dans mes calculs
Re: Un petit calcul de relativité
Je n'ai pas vérifié les applications numériques, mais ça m'a l'air correct.
Victor, essaie de sauter des lignes quand tu fais des calculs, essaie de séparer la partie numérique et calcul, de la partie textuelle.
Victor, essaie de sauter des lignes quand tu fais des calculs, essaie de séparer la partie numérique et calcul, de la partie textuelle.
Re: Un petit calcul de relativité
Le seul petit truc qui me chiffonne
c'est que la lumière parcourt toujours 4.3 AL à C
et que le jumeau parcourt 3 AL à 2/3 de C
Et ceci pour le même référentiel de temps
c'est que la lumière parcourt toujours 4.3 AL à C
et que le jumeau parcourt 3 AL à 2/3 de C
Et ceci pour le même référentiel de temps
Re: Un petit calcul de relativité
Ben moi je ne vois pas de problème.Victor a écrit :Le seul petit truc qui me chiffonne
c'est que la lumière parcourt toujours 4.3 AL à C
et que le jumeau parcourt 3 AL à 2/3 de C
Et ceci pour le même référentiel de temps
Dans le référentiel terrestre, la lumière met 4.3 années pour parcourir cette distance.
Mesuré dans le référentiel du jumeau voyageur, la lumière met 3 années.
Ce ne sont pas les mêmes durées, est-ce qu'il y a contradiction ? NON !
Vue de la terre, l'expérience se déroulant dans le vaisseau du jumeau, on voit que l'horloge utilisée bat moins vite que celle de la terre, d'ailleurs elle retarde, en effet, quand l'horloge du jumeau affiche 3 secondes, l'horloge terrestre affiche 4.3 secondes.
Vue du vaisseau, son horloge marche normalement. Par contre la distance mesurée par le jumeau n'est pas de 4.3 al, mais 3 al. En effet, puisque la terre bouge par rapport au vaisseau, la règle utilisée dans le référentiel terrestre est raccourcie, elle mesure donc une longueur plus grande.
Je pense que tu as oublié de prendre en compte la dilatation relativiste des durées.
Re: Un petit calcul de relativité
Je me suis amusé à faire des calculs avec plusieurs vitesses, obtenant :
On considère un voyage vers Proxima du Centaure à 4.3 al, on veut calculer le temps écoulé pour atteindre Proxima en temps terrestre, et en temps du vaisseau spatial.

Bref on peut continuer le calcul en se rapprochant de plus en plus de la vitesse de la lumière, ce qu'on verra, c'est que le trajet vu depuis la terre va se rapporcher de 4.3 ans (par valeur supérieure).
Par contre pour le vaisseau, ce temps va tendre vers 0.
On considère un voyage vers Proxima du Centaure à 4.3 al, on veut calculer le temps écoulé pour atteindre Proxima en temps terrestre, et en temps du vaisseau spatial.

Bref on peut continuer le calcul en se rapprochant de plus en plus de la vitesse de la lumière, ce qu'on verra, c'est que le trajet vu depuis la terre va se rapporcher de 4.3 ans (par valeur supérieure).
Par contre pour le vaisseau, ce temps va tendre vers 0.
Re: Un petit calcul de relativité
Comme c'est un peu abrupte (un format tableau ça peut être pas mal... je vais faire une image), j'explique comment on arrive à tout ça.
Soit un vaisseau spatial voyageant à une certaine vitesse v par rapport à la terre. Le vaisseau se dirige vers une étoile distante de L0 par rapport à la terre. Cette distance est mesurée dans le référentiel terrestre. Dans le référentiel du vaisseau en mouvement par rapport à la terre, il verra une distance contractée L :

Comme le vaisseau parcourt une distance L0 (mesurée dans le référentiel terrestre) à une vitesse v, en principe, la durée de son voyage dure un certain temps T = L0 / v, où les données sont mesurées dans le référentiel terrestre. Cependant, le vaisseau subit une dilatation relativiste des durées, son voyage dure moins de temps que ce que mesure l'horloge resté au repos sur terre. En effet, l'horloge du vaisseau va indiquer le T0, alors que l'horloge terrestre indiquera T selon la relation :

Si nous faisons un calcul de cohérence nous voyons que :

Au final si nous représentons graphiquement les durées des voyages mesurées dans le référentiel terrestre et du laboratoire, et les longueurs des trajets dans chaque référentiel, nous obtenons la courbe suivante :

Le graphique présente en abscisses le rapport entre la vitesse et la vitesse de la lumière (donc elle varie entre 0 et 1). En ordonnées, j'ai mis les mêmes unités entre la durée (exprimée en années) et la distance exprimée en années lumière (les deux grandeurs sont proportionnelles).
La courbe noire montre la distance mesurée dans le référentiel terrestre, qui est 1 al, et reste constante quelque soit la vitesse.
La courbe violette montre que la distance est de 1 al, mais diminue quand la vitesse augmente, et tend vers 0 lorsque v tend vers c.
La courbe jaune montre la durée du voyage en fonction de la vitesse du vaisseau. A mesure que la vitesse augmente et tend vers c, l'on voit que le temps diminue et tend vers une limite qui est L / c.
Par contre, la courbe cyan est le temps vu par le voyageur. Ce temps diminue comme le temps mesuré sur terre lorsque v est petit par rapport à c, et diminue plus vite que la courbe précédente pour tendre vers 0 lorsque v tend vers c.
Soit un vaisseau spatial voyageant à une certaine vitesse v par rapport à la terre. Le vaisseau se dirige vers une étoile distante de L0 par rapport à la terre. Cette distance est mesurée dans le référentiel terrestre. Dans le référentiel du vaisseau en mouvement par rapport à la terre, il verra une distance contractée L :

Comme le vaisseau parcourt une distance L0 (mesurée dans le référentiel terrestre) à une vitesse v, en principe, la durée de son voyage dure un certain temps T = L0 / v, où les données sont mesurées dans le référentiel terrestre. Cependant, le vaisseau subit une dilatation relativiste des durées, son voyage dure moins de temps que ce que mesure l'horloge resté au repos sur terre. En effet, l'horloge du vaisseau va indiquer le T0, alors que l'horloge terrestre indiquera T selon la relation :

Si nous faisons un calcul de cohérence nous voyons que :

Au final si nous représentons graphiquement les durées des voyages mesurées dans le référentiel terrestre et du laboratoire, et les longueurs des trajets dans chaque référentiel, nous obtenons la courbe suivante :

Le graphique présente en abscisses le rapport entre la vitesse et la vitesse de la lumière (donc elle varie entre 0 et 1). En ordonnées, j'ai mis les mêmes unités entre la durée (exprimée en années) et la distance exprimée en années lumière (les deux grandeurs sont proportionnelles).
La courbe noire montre la distance mesurée dans le référentiel terrestre, qui est 1 al, et reste constante quelque soit la vitesse.
La courbe violette montre que la distance est de 1 al, mais diminue quand la vitesse augmente, et tend vers 0 lorsque v tend vers c.
La courbe jaune montre la durée du voyage en fonction de la vitesse du vaisseau. A mesure que la vitesse augmente et tend vers c, l'on voit que le temps diminue et tend vers une limite qui est L / c.
Par contre, la courbe cyan est le temps vu par le voyageur. Ce temps diminue comme le temps mesuré sur terre lorsque v est petit par rapport à c, et diminue plus vite que la courbe précédente pour tendre vers 0 lorsque v tend vers c.
Re: Un petit calcul de relativité
Victor ?
Est-ce que j'ai répondu à ta question ?
Je me suis donné du mal pour écrire des équations et faire des courbes ça te plaît ?
ça te plaît ? 
Est-ce que j'ai répondu à ta question ?

Je me suis donné du mal pour écrire des équations et faire des courbes
 ça te plaît ?
ça te plaît ? 
Re: Un petit calcul de relativité
Oui Bongo et merci m'sieur!...
Question subsidiaire comment peut on parler de causalité avec deux repère différents
le jumeau sur terre et le jumeau voyageur n'ont plus la même chaine de causalité temporelle
Question subsidiaire comment peut on parler de causalité avec deux repère différents
le jumeau sur terre et le jumeau voyageur n'ont plus la même chaine de causalité temporelle
Re: Un petit calcul de relativité
La causalité dit que la cause précède la conséquence. Ceci est trivial dans le cadre de la physique classique où le temps est universel. Cependant, je te l'accorde, la relativité introduit une subtilité.
En relativité, l'on parle d'évènements caractérisés par 4 coordonnées une temporelle et 3 autres spatiales.
Il se trouve que lorsque deux évènements sont causales, alors il est possible de les relier par un rayon lumineux, ce qui veut dire que pour deux évènements A et B tu as :
c²(tB_tA)² > (xB-xA)² + (yB-yA)² + (zB-zA)²
Bon j'espère que j'ai largué personne. L'équation ci-dessus veut juste dire qu'un signal lumineux a le temps de relier les deux évènements, ou en d'autres termes, il faut une vitesse inférieure ou égale à c pour passer de (tA,xA,yA,zA) à (tB,xB,yB,zB). En terme vulgarisé, vous êtes sur terre, et vous devez vous rendre à un rendez-vous sur Mars dans 2 minutes, est-ce que vous pouvez le faire ? (même à la vitesse de lumière nous ne pourrez pas).
Le diagramme suivant traduit l'équation que j'ai écrite :
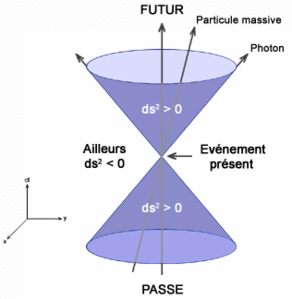
Cela traduit que si un point est dans le cône bleu, alors les deux évènements sont causalement reliés, sinon ils ne le sont pas.
Donc maintenant que j'ai introduit cette notion d'évènement causal, en relativité, on montre que lors d'un changement de référentiel :
- soit 2 deux évènements causaux, A et B, tels que A précède B, alors dans tout référentiel, A précède B
- pour deux évènements non causaux, A et B, il est possible de trouver un référentiel où A précède B, ou B précède A, ou A et B sont simultanés.
Pour la 2ème remarque, ce n'est pas grave, c'est deux évènements sont non causaux, que A précède B ou l'inverse, cela n'a pas d'influence, puisque les deux évènements ne peuvent s'influencer l'un l'autre.
En relativité, l'on parle d'évènements caractérisés par 4 coordonnées une temporelle et 3 autres spatiales.
Il se trouve que lorsque deux évènements sont causales, alors il est possible de les relier par un rayon lumineux, ce qui veut dire que pour deux évènements A et B tu as :
c²(tB_tA)² > (xB-xA)² + (yB-yA)² + (zB-zA)²
Bon j'espère que j'ai largué personne. L'équation ci-dessus veut juste dire qu'un signal lumineux a le temps de relier les deux évènements, ou en d'autres termes, il faut une vitesse inférieure ou égale à c pour passer de (tA,xA,yA,zA) à (tB,xB,yB,zB). En terme vulgarisé, vous êtes sur terre, et vous devez vous rendre à un rendez-vous sur Mars dans 2 minutes, est-ce que vous pouvez le faire ? (même à la vitesse de lumière nous ne pourrez pas).
Le diagramme suivant traduit l'équation que j'ai écrite :

Cela traduit que si un point est dans le cône bleu, alors les deux évènements sont causalement reliés, sinon ils ne le sont pas.
Donc maintenant que j'ai introduit cette notion d'évènement causal, en relativité, on montre que lors d'un changement de référentiel :
- soit 2 deux évènements causaux, A et B, tels que A précède B, alors dans tout référentiel, A précède B
- pour deux évènements non causaux, A et B, il est possible de trouver un référentiel où A précède B, ou B précède A, ou A et B sont simultanés.
Pour la 2ème remarque, ce n'est pas grave, c'est deux évènements sont non causaux, que A précède B ou l'inverse, cela n'a pas d'influence, puisque les deux évènements ne peuvent s'influencer l'un l'autre.
Re: Un petit calcul de relativité
Pourtant en mécanique quantique les relations de cause à effet ne dépendent pas de C,
des photons corrélés se moque bien de C et le paradoxe est:
Qui a raison entre la RG et la quantique
s'il existe des interaction allant plus vite que C
des photons corrélés se moque bien de C et le paradoxe est:
Qui a raison entre la RG et la quantique
s'il existe des interaction allant plus vite que C
Re: Un petit calcul de relativité
La mécanique quantique ne contredit en rien la relativité. Quant à l'intrication quantique, il n'y a aucun signal transmis plus vite que c.
Re: Un petit calcul de relativité
Bonjour!
Eh ben ! Très intéressant tes petits calculs !
Je ne comprends pas tout !
La cause ne peut pas produire un effet plus vite que la lumière …
Si le « phénomène induisant » et le « phénomène induit » sont distants de d, il y a un temps de réponse = c*d ?
L’intrication quantique ? Pour connaître l’état du demi photon de gauche, il faut une information, alors on « agit » sur ce demi photon, pour savoir dans quel état il se trouve ; et du coup on sait immédiatement dans quel état est le demi photon de droite(1) : on a donc une information à distance instantanée ! Non ?
Dit autrement : on dispose d’une information à distance, non transmise physiquement ???(Mes neurones s’entrechoquent ! la contradiction est bien là ?)
Pour le béotien que je suis, couper un photon en 2 est déjà une bizarrerie(2) ; Je m’attendais à ce qu’un miroir semi-transparent, à « argenture granuleuse », réfléchisse statistiquement un photon sur2 ! En plus une réflexion ça maltraite le photon ? (ça polarise ?)
(1) Plus fort, on « agit » instantanément sur ce demi-photon !
(2) Je crois que je n’ai pas du comprendre ce qu’était un photon ! n’est ce pas un quantum d’énergie ?un quantum, ça ne se coupe pas !
Eh ben ! Très intéressant tes petits calculs !
Je ne comprends pas tout !
La cause ne peut pas produire un effet plus vite que la lumière …
Si le « phénomène induisant » et le « phénomène induit » sont distants de d, il y a un temps de réponse = c*d ?
L’intrication quantique ? Pour connaître l’état du demi photon de gauche, il faut une information, alors on « agit » sur ce demi photon, pour savoir dans quel état il se trouve ; et du coup on sait immédiatement dans quel état est le demi photon de droite(1) : on a donc une information à distance instantanée ! Non ?
Dit autrement : on dispose d’une information à distance, non transmise physiquement ???(Mes neurones s’entrechoquent ! la contradiction est bien là ?)
Pour le béotien que je suis, couper un photon en 2 est déjà une bizarrerie(2) ; Je m’attendais à ce qu’un miroir semi-transparent, à « argenture granuleuse », réfléchisse statistiquement un photon sur2 ! En plus une réflexion ça maltraite le photon ? (ça polarise ?)
(1) Plus fort, on « agit » instantanément sur ce demi-photon !
(2) Je crois que je n’ai pas du comprendre ce qu’était un photon ! n’est ce pas un quantum d’énergie ?un quantum, ça ne se coupe pas !
Re: Un petit calcul de relativité
le temps de réponse est d/c pour être précis.Nodarp a écrit :Bonjour!
Eh ben ! Très intéressant tes petits calculs !
Je ne comprends pas tout !
La cause ne peut pas produire un effet plus vite que la lumière …
Si le « phénomène induisant » et le « phénomène induit » sont distants de d, il y a un temps de réponse = c*d ?
Non non on ne coupe pas un photon en deux, je ne comprends pas trop ton expérience. Et je ne vois pas où est l'action instantanée. Quand tu mesures l'état d'un photon, tu ne fais que constater dans quel état il est, tu n'agis en aucune façon sur son état puisque la mesure est soumise aux probabilités.Nodarp a écrit : L’intrication quantique ? Pour connaître l’état du demi photon de gauche, il faut une information, alors on « agit » sur ce demi photon, pour savoir dans quel état il se trouve ; et du coup on sait immédiatement dans quel état est le demi photon de droite(1) : on a donc une information à distance instantanée ! Non ?
Dit autrement : on dispose d’une information à distance, non transmise physiquement ???(Mes neurones s’entrechoquent ! la contradiction est bien là ?)
Un miroir semi-transparent laisse passer un photon sur deux. Ca veut dire que pour un photon, il a une probabilité de 0.5 d'être réfléchi et 05 d'être transmis.Nodarp a écrit : Pour le béotien que je suis, couper un photon en 2 est déjà une bizarrerie(2) ; Je m’attendais à ce qu’un miroir semi-transparent, à « argenture granuleuse », réfléchisse statistiquement un photon sur2 ! En plus une réflexion ça maltraite le photon ? (ça polarise ?)
Si tu mesures que le photon est passé à gauche, tu sais instantanément qu'il n'est pas passé à droite et vice versa. Je ne vois pas où on contredit le principe de causalité.
Nodarp a écrit :(1) Plus fort, on « agit » instantanément sur ce demi-photon !
(2) Je crois que je n’ai pas du comprendre ce qu’était un photon ! n’est ce pas un quantum d’énergie ?un quantum, ça ne se coupe pas !
Re: Un petit calcul de relativité
Bonjour!
Me voilà rassuré : on ne coupe pas un photon en 2! dès lors il n’ya aucun problème effectivement !
Sauf que je n’ai rien compris à l’intrication quantique !!!
Je m’y replonge !
Merci pour ta réponse!
Me voilà rassuré : on ne coupe pas un photon en 2! dès lors il n’ya aucun problème effectivement !
Sauf que je n’ai rien compris à l’intrication quantique !!!
Je m’y replonge !
Merci pour ta réponse!
Re: Un petit calcul de relativité
Dans les faits c'est l'information photons/corrélés qui se conserve dans le temps et non pas une information qui voyagerait