Âge caractéristique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En astronomie l'âge caractéristique d'un pulsar est une estimation de son âge réel par la mesure du ralentissement de sa période de rotation. Il donne un ordre de grandeur de l'âge réel du pulsar sous certaines conditions.
Définition de l'âge caractéristique
Connaissant la période P de rotation d'un pulsar et sa variation temporelle dP / dt, notée
- .
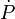
Cette formule est obtenue en supposant que le ralentissement du pulsar est dû au rayonnement dipolaire magnétique résultant de sa rotation
L'énergie cinétique de rotation d'un objet est donnée par la formule
-
où I est le moment d'inertie et ω la vitesse angulaire, reliée à la période par la formule P = 2π / ω. Dans le cas où les pertes d'énergie sont dues à un rayonnement dipolaire, on a la formule bien connue
-
la valeur de la constante de proportionnalité, négative, étant ici sans importance. De ces deux formules, on tire
-
qui se réécrit en
-
la quantité t * étant une constant d'intégration à déterminer. La période P évolue donc selon
-
Partant de
-
Dans l'hypothèse où la valeur initiale de la période est négligeable (ce qui revient à dire que le pulsar est né en t = t * ), alors l'âge du pulsar correspond bien à
-
Autre méthode d'estimation de l'âge
Il existe une autre méthode d'estimation de l'âge des pulsars, en pratique uniquement utilisable pour les pulsars de notre Galaxie, appelée âge cinématique. Dans ce cas, on estime le temps qu'il a fallu au pulsar pour quitter le plan galactique, son lieu probable de naissance, pour se trouver dans sa position actuelle. Cette méthode nécessite en pratique de mesurer essentiellement le mouvement propre du pulsar, c'est-à-dire son déplacement sur la sphère céleste. Cette méthode est observationnellement plus entachée d'incertitude que l'âge caractéristique, du fait de la petitesse du mouvement propre, mais pourrait être moins sujette à des erreurs systématiques si l'indice de freinage n'est pas constant au cours du temps, aussi est-elle considérée comme complémentaire à celle-ci.
Précision de l'estimation
Il existe plusieurs effets qui peuvent entacher, parfois de façon dramatique, cette estimation de l'âge caractéristique d'un pulsar
Pulsar jeune
L'âge caractéristique est calculé dans l'hypothèse où la période actuelle est grande devant la période initiale du pulsar (a priori inconnue). Plus le pulsar est jeune, plus cette approximation est incorrecte. Si l'on tient compte de la valeur de la période initiale P0 du pulsar, alors son âge caractéristique correspond à
-
![t = \frac{1}{2} \frac{P}{\dot P} \left[1 - \left(\frac{P_0}{P} \right)^2 \right]](https://static.techno-science.net/illustration/Definitions/autres/0/053131301173c37b5a6c0cb369da28fb_aa09d98d349de2fb71d9a7a45b2890cf.png)
![t = \frac{1}{2} \frac{P}{\dot P} \left[1 - \left(\frac{P_0}{P} \right)^2 \right]](https://static.techno-science.net/illustrationWebp/Definitions/autres/0/053131301173c37b5a6c0cb369da28fb_aa09d98d349de2fb71d9a7a45b2890cf.png)
Dans le cas où l'âge du pulsar est connu (comme le pulsar du Crabe), ceci permet en fait de remonter à sa période de rotation initiale, t étant cette fois non pas l'âge caractéristique, mais l'âge vrai (environ 950 ans pour le pulsar du Crabe, qui est cependant un mauvais exemple ici, car son rayonnement n'est pas dipolaire, voir ci-dessous).
La démonstration est identique à celle ci-dessus, si ce n'est que la naissance du pulsar, en t = t0 est prise en compte. On note donc
-
que l'on peut réécrire en
-
ou bien
-
L'âge du pulsar est t − t0 La formule donnant la dérivée est toujours
-
d'où à nouveau
-
qui combiné avec la formule faisant intervenir la période initiale du pulsar donne
-
![t - t_0 = \frac{1}{2} \frac{P}{\dot P} \left[1 - \left(\frac{P_0}{P}\right)^2\right]](https://static.techno-science.net/illustration/Definitions/autres/f/f7a26ce6191c9f68de1729eb54079961_1009d41b8147d6e43f238d61fef93bdf.png)
![t - t_0 = \frac{1}{2} \frac{P}{\dot P} \left[1 - \left(\frac{P_0}{P}\right)^2\right]](https://static.techno-science.net/illustrationWebp/Definitions/autres/f/f7a26ce6191c9f68de1729eb54079961_1009d41b8147d6e43f238d61fef93bdf.png)
La prise en compte de la valeur de la période initiale peut considérablement affecter l'estimation de l'âge. Pour PSR J0205+6449, le pulsar central de la nébuleuse 3C 58, rémanent de la supernova historique SN 1181, l'âge caractéristique trouvé sans tenir compte de la période initiale donne environ 5400 ans, alors que l'âge réel du pulsar est d'environ 830 ans. Un tel cas permet en fait de trouver la valeur initiale de la période à partir de l'âge caractéristique, connaissant l'âge vrai du pulsar (65,58 ms pour la période actuelle, et environ 60 ms pour la période initiale).
Rayonnement non dipolaire
Il est possible que l'approximation d'un dipôle tournant ne soit pas bonne pour un pulsar. On ne peut pas bien sûr observer directement la structure du champ magnétique du pulsar, mais on peut observer sur le long terme l'évolution de sa période de rotation. Dans la situation où celle-ci évolue suffisamment vite, on peut non seulement connaître sa dérivée temporelle
-
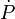
Dans le cas d'un rayonnement dipolaire, l'indice de freinage vaut n = 3. S'il ne vaut pas 3, alors l'âge caractéristique est donné par
-
et en tenant compte de la valeur de la période initiale,
-
![t_c = \frac{1}{n - 1} \frac{P}{\dot P} \left[1 - \left(\frac{P_0}{P}\right)^{n - 1} \right]](https://static.techno-science.net/illustration/Definitions/autres/f/f22f12409c86a0ee2b9c29b37e6ca255_0e9e768d57cb4f0fc28d2e39b42a7ac2.png)
![t_c = \frac{1}{n - 1} \frac{P}{\dot P} \left[1 - \left(\frac{P_0}{P}\right)^{n - 1} \right]](https://static.techno-science.net/illustrationWebp/Definitions/autres/f/f22f12409c86a0ee2b9c29b37e6ca255_0e9e768d57cb4f0fc28d2e39b42a7ac2.png)
Pulsar milliseconde
L'âge caractéristique, défini en prenant compte ou non de la valeur de l'indice de freinage, suppose implicitement que le ralentissement du pulsar a toujours été dû à la même cause, et qu'aucun autre processus physique n'a affecté sa rotation. On sait en pratique que ces hypothèses sont fausses pour les pulsars millisecondes, dont la rotation a été considérablement accélérée après que le champ magnétique du pulsar ait décru. Dans de telles situations, la valeur de l'âge caractéristique ne correspond à rien.
