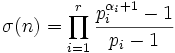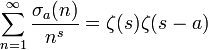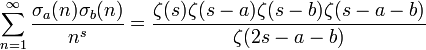Fonction diviseur - Définition

En mathématiques, la fonction diviseur σ_a(n) est définie comme la somme des a-ièmes puissances des diviseurs de n, où

La notation d(n) est aussi utilisée pour noter σ₀(n), ou le nombre de diviseurs de n. La fonction sigma σ(n) est

.

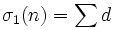Par exemple si p est un nombre premier,

car, par définition, les facteurs d'un nombre premiers sont 1 et lui-même.

Généralement, la fonction diviseur est multiplicative, mais n'est pas complètement multiplicative.

La conséquence de ceci, si nous écrivons

alors nous avons

Nous notons aussi

.

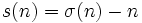Cette fonction est utilisée pour reconnaître les nombres parfaits qui ont, pour n

.

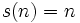Par exemple, pour deux nombres premiers distincts p et q, soit

Alors

Deux séries de Dirichlet impliquant la fonction diviseur sont :

et