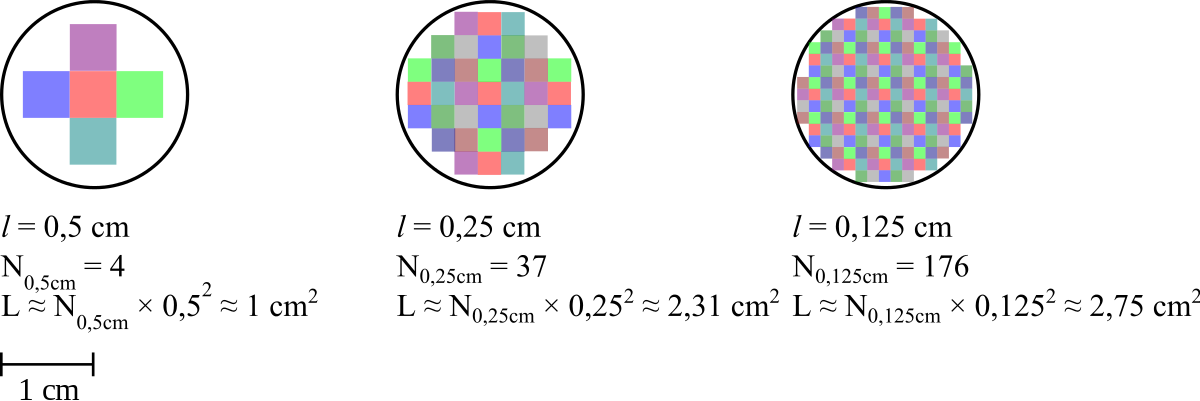Dimension - Définition

Dans le sens commun, la notion de dimension renvoie à la taille ; les dimensions d'une pièce sont sa longueur, sa largeur et sa profondeur/son épaisseur, ou bien son diamètre si c'est une pièce de révolution.

En physique et en mathématique, la notion de dimension est bien particulière. Ces notions ont été détournées dans le domaine de la science-fiction.

Technique

Dans le domaine de la mécanique, le terme " dimension " renvoit à la taille d'une pièce.

Dans l'absolu, les dimensions d'une pièce peuvent être choisies de manière totalement arbitraire, l'important étant qu'elles soient compatibles avec l'utilisation finale de la pièce.

Dans un but de normalisation, il est toutefois préférable d'utiliser comme dimensions linéaires nominales des valeurs de la " série de Renard ".

Dans la pratique de tous les jours, le terme " dimension " renvoit à la taille d'un objet.
Exemple et définition:

• Objet de: 350 x 250 x 255 mm.
  
• Description: (L)ongeur x (l)argeur x (h)auteur.
  
• Forme: D = (L x l x h)

Physique

En physique, le terme dimension regroupe deux notions complètement différentes.

Dimension d'un espace vectoriel

La physique utilise beaucoup la notion mathématique d'espace vectoriel. On peut vulgariser cette notion en disant que

la dimension d'un espace est le nombre de variables qui servent à définir un état, un événement.

Ainsi par exemple, on dit classiquement que notre univers est à quatre dimensions, puisqu'un événement se définit par la position dans l'espace (x, y, z) et l'instant t auquel cet événement survient.

• Un objet volumique constant (c'est-à-dire dont les propriétés sont indépendantes du temps, du moins durant l'étude) est dit à trois dimensions, car il faut trois nombres (x, y, z) pour désigner un de ses points au sein de l'objet ;
• un objet plan (comme une feuille de papier) dont on néglige l'épaisseur est dit à deux dimensions, car il faut deux nombres (x, y) pour désigner un de ses points au sein de l'objet ;
• un objet linéaire (comme un fil) dont on néglige l'épaisseur est dit à une dimension, car il suffit d'un seul nombre x pour désigner un de ses points au sein de l'objet (abscisse curviligne) ;
• un objet ponctuel (comme un point) dont on néglige la taille est dit de dimension zéro, car une fois que l'on a désigné le point, on n'a besoin d'aucun paramètre pour trouver le point...

Ces concepts sont repris en modélisation informatique (objet 2D, 3D).

Cette notion est la traduction de la notion mathématique de dimension (voir plus bas).

Dimension d'une grandeur

La dimension d'une grandeur physique est son unité exprimée par rapport aux sept unités de base du système international. On retraduit les unités en grandeurs.

Par exemple, la vitesse a la dimension d'une longueur divisée par un temps (c'est-à-dire que l'unité de vitesse est le mètre par seconde).

Mathématiques

Dimension d'un espace vectoriel

En mathématiques, la notion de dimension correspond à la dimension de l' espace vectoriel de la physique :

si un espace vectoriel est muni d'une base de cardinal fini d, alors toutes les bases de cet espace ont pour cardinal d, et la dimension de cet espace est d.

(Rappelons qu'une base est une famille libre et génératrice de l'espace vectoriel, c'est-à-dire que tout vecteur peut se décomposer en une unique combinaison linéaire des vecteurs de cette famille.) Ceci est une conséquence du lemme de Steinitz :

si un espace vectoriel possède une famille génératrice finie de n vecteurs, toute famille de plus de n vecteurs est liée.

Lorsqu'un espace vectoriel n'admet aucune base de cardinal fini, on dit qu'il est de " dimension infinie ". Exemple : l'ensemble des suites réelles est un espace vectoriel de dimension infinie. Dans un tel espace il existe des familles libres finies arbitrairement grandes, mais aucune famille génératrice finie.

Dimension fractale

Mais la définition de la dimension donnée ci-dessus est insuffisante, notamment dans le cas des fractales.

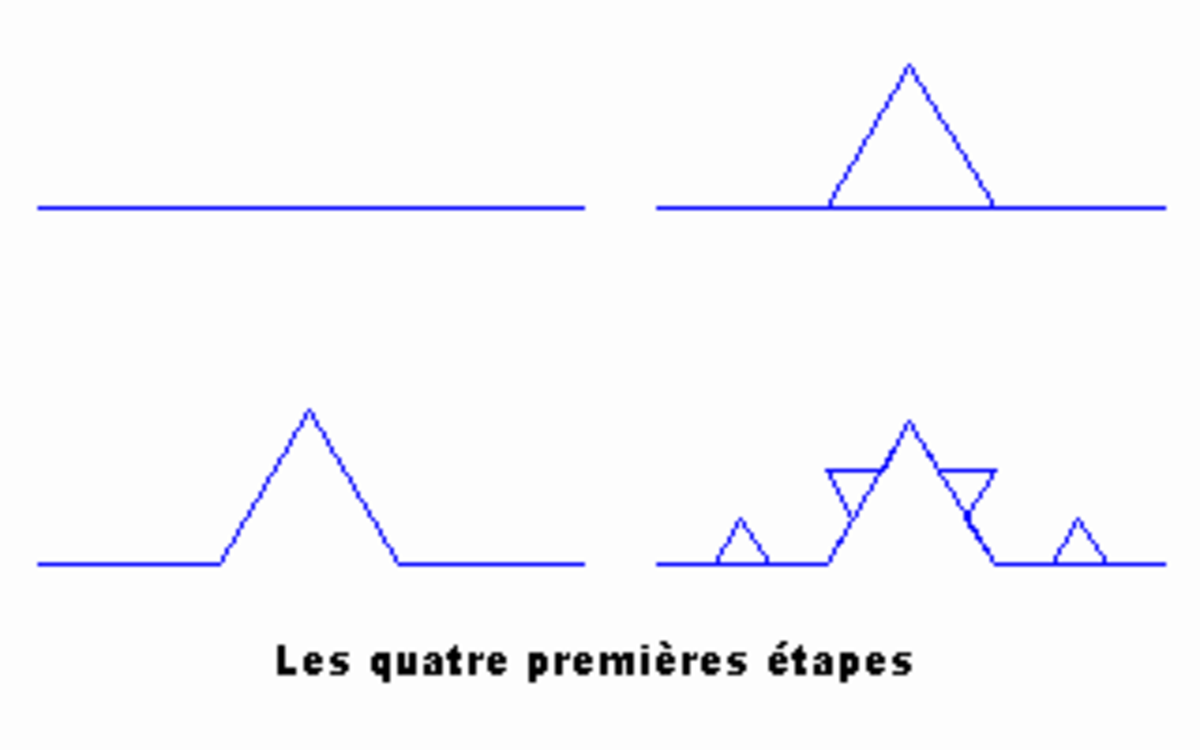
De manière simplifiée et en première approximation (Cf. l'article spécialisé pour une meilleure définition), un objet fractal est un objet ayant une homothétie interne, c'est-à-dire qu'une portion de l'objet est identique à l'objet complet. Considérons un exemple simple, la courbe de von Koch : cette courbe est construite de manière récursive, on part d'un segment de droite, et on remplace chaque segment par un segment avec un chevron au milieu.

On répète cette opération à l'infini. Cette courbe est une ligne (donc de dimension 1, au sens ordinaire). Sa longueur est infinie, puisqu'à chaque étape on multiplie sa longueur par 4/3, et qu'il y a un nombre infini d'étapes. Pourtant, et contrairement à une droite infinie, on peut toujours trouver une courbe de longueur finie aussi proche que l'on veut de la courbe de von Koch. On peut donc dire en fait que si on trouve que la longueur de la courbe de von Koch est infinie, c'est qu'on l'évalue dans une " mauvaise " dimension, et qu'en mesurant " mieux ", on aurait une mesure " utile ", finie.

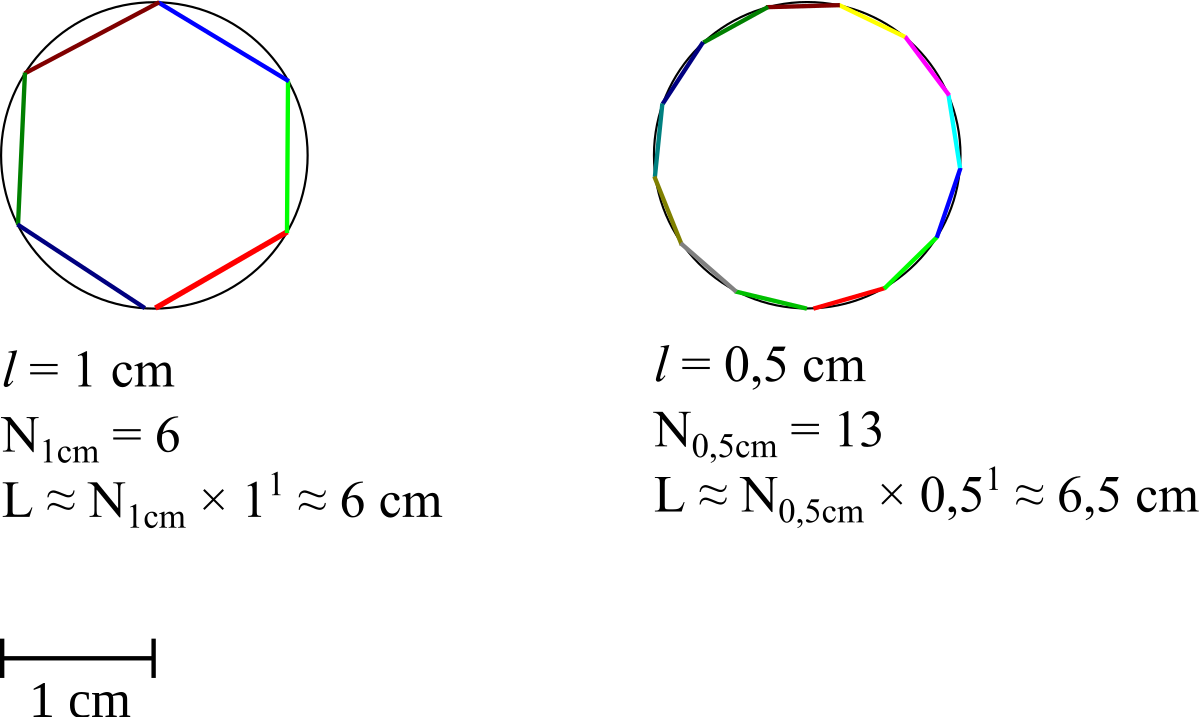
Nous avons besoin de revenir sur la notion d'étalon en physique :

• l'étalon de longueur est une règle de longueur fixe (dimension 1) : pour mesurer une longueur, on regarde combien de règles tiennent bout-à-bout sur la courbe ;
• l'étalon de surface est un carreau (carré) de côté fixe (dimension 2) : pour mesurer la surface, on regarde combien de carreaux ou peut poser côte-à-côte sur la surface ;
• l'étalon de volume est un pavé (cube) d'arrête fixe (dimension 3) : pour mesurer le volume, on regarde combien de pavés on peut empiler dans l'objet.

On ne peut évaluer la longueur que d'un objet de dimension 1 : même en prenant une règle minuscule, un point ne pourra jamais la contenir, et à l'inverse sur une surface, on peut mettre un nombre infini de règles côte-à-côte (celles-ci ont une épaisseur nulle).

De même, on ne peut évaluer l'aire que d'un objet de dimension 2 : un point ou une courbe ne pourra jamais être pavé par des carreaux (même très petits), et dans un volume, on peut empiler un nombre infini de carreaux (ceux-ci ont une épaisseur nulle).

On ne peut évaluer le volume que d'un objet à trois dimension, puisqu'on ne peut pas mettre de pavé dans un point, une courbe ni une surface.

Ainsi, si l'on appelle d_o la dimension de l'objet et d_e celle de l'étalon, on a :

• si d_e > d_o, la mesure donne 0 : on ne peut pas mettre un seul étalon dans l'objet ; c'est le cas pour la courbe de von Koch lorsqu'on utilise une mesure avec une aire, ce qui indique donc que sa dimension fractale est strictement inférieure à 2.
• si d_e < d_o, la mesure donne ∞ : on peut mettre autant d'étalon qu'on veut dans l'objet ; c'est le cas pour la courbe de von Koch lorsqu'on utilise une mesure avec une longueur, ce qui indique donc que sa dimension fractale est strictement supérieure à 1.
• si d_e = d_o, la mesure peut donner (si l'objet mesuré n'est pas infini) un nombre fini, le nombre d'étalon qu'il faut pour couvrir l'objet ; notre problème est donc de trouver (si elle existe) la " bonne " dimension, celle qui nous donnera une mesure finie (si l'objet est fini, bien sur).

Pour faire cette mesure, la " taille " de l'étalon n'est pas sans effet. Si l'étalon est trop grand, il ne rentre pas dans l'objet (la mesure est nulle), mais en prenant des étalons de plus en plus petits, on obtient (d'habitude) des mesures qui se rapprochent. Si, pour mesurer une ligne, on utilise une règle de longueur ?, plus ? est petit, plus on pourra mettre d'étalons dans l'objet à mesurer. La mesure est le produit du nombre d'étalons par la taille de l'étalon : Si l'on fait tenir N_? règles de longueur ?, la mesure sera

M(?) = N_?×?

Pour un carreau de côté ?, l'aire du carreau sera ?², et si l'on couvre la surface de N_? carreaux, la mesure sera

M(?) = N_?×?²

Pour un pavé d'arrête ?, le volume du pavé sera ?³, et si l'on rempli l'objet de N_? pavés, la mesure sera

M(?) = N_?×?³

On voit que la dimension est aussi l'exposant intervenant dans le calcul de la mesure.

Dans le cas d'une ligne habituelle, lorsqu'on utilise une règle de longueur ? divisée par deux (ou par trois, quatre,… N), on peut mettre à peu près deux (respectivement trois, quatre,… N) fois plus de fois l'étalon dans l'objet : la mesure ne change presque pas, et finalement, au fur et à mesure qu'on réduit la taille de l'étalon, on obtient une suite de mesures qui converge : la longueur exacte de la courbe est la limite de M(?) lorsque ? tend vers 0, c'est un nombre réel.

Prenons l'exemple d'une surface ; lorsqu'on la pave des carreaux, on n'obtient qu'une approximation de son aire (on approche la surface par un polygone). Si l'on fait tenir N_? règles de longueur ?, la mesure sera

M(?) = N_?×? ²

L'aire longueur exacte de la courbe est la limite de M(?) lorsque ? tend vers 0. Par contre

M(?) = N_?×?

tend vers +∞, et

M(?) = N_?×? ³

tend vers 0. On retrouve par le calcul ce que l'on a établi par géométrie.

Dans le cas de la courbe de von Koch, on voit bien que lorsqu'on divise l'étalon de longueur par 3, on peut mettre 4 fois plus d'étalon. Du coup, la suite de mesures de longueur

M(?/3) = N_?/3 ×(?/3) ¹ = 4N_? ×? ¹/3 = 4/3 × M(?) > M(?)

ne converge pas et la suite de mesures d'aire

M(?/3) = N_?/3 ×(?/3) ² = 4N_?/3 ×? ²/9 = 4/9 × M(?) < M(?)

tend vers 0.

Mais il est possible d'imaginer une dimension fractionnaire, de faire varier de façon continue la " dimension ". Et de fait, pour la dimension

d_o = log 4/log 3 ≈ 1,261 9.

on peut faire converger la mesure pour la courbe de von Koch en prenant :

M(?) = N_? ×? ^do

Ceci peut être représenté de manière plus rigoureuse par la dimension d'Hausdorff-Besicovitch.

Dimension topologique

La dimension topologique, définie par récurrence, associe à chaque partie P de Rⁿ un entier, égal à la dimension algébrique si P est un sous-espace affine, à n si P est d'intérieur non vide, à 1 si P est une courbe régulière, à 2 si P est une surface régulière, etc. De manière générale elle attribue à un ensemble usuel sa dimension intuitive qui est le nombre de variables indépendantes nécessaire pour le décrire.

Dimension de Hausdorff - Besicovitch

La dimension d'Hausdorff-Besicovitch D_h prend sa définition par le quotient logarithmique entre un nombre d'homothéties internes d'un objet, sur l'inverse de la raison de cette homothétie. Donc,

.

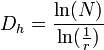On aura donc, pour un point :

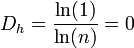avec n naturel > 1,

vu qu'on peut établir un point par une homothétie interne de raison n. On peut dire " un point est le produit de n homothéties internes de ce même point, de raison n ".

Avec une droite (segment), il peut s'établir avec deux homothéties internes de raison 1/2, donc

.

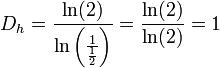De cette façon, on trouve pour les formes et objets euclidiens, un isomorphisme entre ces deux dimensions établies. Cependant, des grandes différences se présentent avec les fractales.

Dimension de Minkowski - Bouligand

La dimension de Minkowski-Bouligand D_m est le quotient logarithmique entre le volume de boules dont on a besoin pour recouvrir n'importe quel objet euclidien, ou non euclidien (de rayon le plus petit possible), qui peut se renfermer dans une boule de rayon r, avec le quotient des rayons. On obtient alors,

,

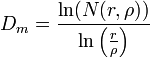où r est le rayon de la boule extérieure, qui se trouve recouverte par des boules plus petites de rayon ρ. N(r,ρ) désigne l'aire ou volume de la boule ou disque qui recouvre cette figure.

Dimension combinatoire d'un espace topologique

Cette autre notion de dimension est surtout utile dans le cas des schémas, où la topologie, en un certain sens, est d'une nature plus combinatoire que géométrique.

Dans les œuvres de science-fiction

Dans le domaine de la science-fiction, la quatrième dimension désigne, soit une quatrième dimension spatiale (en ajout avec la longueur, la largeur et la hauteur) qui serait responsables de faits insolites (cf: Théorie d'Everett ); soit une autre dimension, celle-ci, temporelle et non spatiale : c' est à dire le temps à travers lequel les protagonistes pourraient voyager (cf : vitesse supraluminique ). Par extension, le terme " dimension " a finalement été utilisé pour caractériser les mondes dits " parallèles ", c'est-à-dire par lesquels on ne peut pas accéder en voyageant dans l'espace ; on ne peut y accéder qu'en utilisant un appareil ouvrant une " faille " entre les " dimensions ", ou bien à l'occasion d'un événement accidentel. On dit que le monde parallèle est situé dans une " autre dimension ".

Articles de mathématiques en rapport avec l'algèbre linéaire

Espace vectoriel | Base | Dimension | Matrice | Application linéaire | Déterminant | Trace | Rang | Théorème des facteurs invariants | Réduction d'endomorphisme | Réduction de Jordan | Décomposition de Dunford | Valeur propre | Polynôme caractéristique | Forme linéaire | Espace dual | Orthogonalité | Produit scalaire | Produit vectoriel | Polynôme d'endomorphisme | Polynôme minimal | Tenseur | Pseudovecteur | Covecteur | Algèbre multilinéaire

Modifier

Articles de mathématiques en rapport avec l'algèbre bilinéaire

Espace euclidien | Forme bilinéaire | Forme quadratique | Forme sesquilinéaire | Orthogonalité | Base orthonormale | Projection orthogonale | Inégalité de Cauchy-Schwarz | Inégalité de Minkowski | Matrice définie positive | Matrice semi-définie positive | Décomposition QR | Déterminant de Gram | Hermitien | Espace de Hilbert | Base de Hilbert | Théorème spectral | Théorème de Stampacchia | Théorème de Riesz | Théorème de Lax-Milgram | Théorème de représentation de Riesz

Modifier