Courbe elliptique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, une courbe elliptique est un cas particulier de courbe algébrique, munie entre autres propriétés d'une addition géométrique sur ses points.
Les courbes elliptiques ont de nombreuses applications dans des domaines très différents des mathématiques : elles interviennent ainsi en mécanique classique dans la description du mouvement des toupies, en théorie des nombres dans la preuve du dernier théorème de Fermat, en cryptologie dans le problème de la factorisation des entiers ou pour fabriquer des codes performants.
Contrairement à ce que son nom pourrait laisser croire, l'ellipse n'est pas une courbe elliptique. Le nom des courbes elliptiques vient historiquement de leur association avec les intégrales elliptiques, elles-mêmes appelées ainsi car elles servent en particulier à calculer la longueur d'arcs d'ellipses.
À l'aide d'un choix adapté de coordonnées, une courbe elliptique peut être représentée dans un plan par une équation cubique de la forme :
Les coefficients ![]() ,
, ![]() ,
, ![]() ,
, ![]() et
et ![]() sont des éléments du corps
sont des éléments du corps ![]() sur lequel est définie la courbe, mais ils ne sont pas déterminés par la courbe de manière unique. Réciproquement, pour qu'une telle équation décrive effectivement une courbe elliptique, il faut que la courbe ainsi définie ne soit pas singulière, c’est-à-dire qu'elle n'ait ni point de rebroussement, ni point double.
sur lequel est définie la courbe, mais ils ne sont pas déterminés par la courbe de manière unique. Réciproquement, pour qu'une telle équation décrive effectivement une courbe elliptique, il faut que la courbe ainsi définie ne soit pas singulière, c’est-à-dire qu'elle n'ait ni point de rebroussement, ni point double.
Les points de la courbe sur un corps ![]() (contenant
(contenant ![]() ) ont pour coordonnées les solutions
) ont pour coordonnées les solutions ![]() dans
dans ![]() de l'équation ; on y joint un point à l'infini (l'élément zéro de l'addition). On note cet ensemble de points
de l'équation ; on y joint un point à l'infini (l'élément zéro de l'addition). On note cet ensemble de points ![]() .
.
Formellement, une courbe elliptique est une courbe algébrique projective non-singulière de genre 1 sur un corps ![]() et dont un point à coordonnées dans
et dont un point à coordonnées dans ![]() est spécifié.
est spécifié.
Même si certaines constructions ou certaines propriétés comme l'addition des points sont communes à toutes, la description des courbes elliptiques, ainsi que leurs applications possibles, dépend beaucoup du corps de définition choisi.
Courbes elliptiques sur les nombres réels
Il est possible de décrire concrètement les courbes elliptiques sur les nombres réels, et de définir en particulier l'addition des points, avec les connaissances d'un étudiant au niveau lycée. Dans cette section, le cadre est celui du plan réel euclidien, les points considérés ont des coordonnées x, y réelles, les droites et les courbes sont définies par des équations à coefficients réels. Pour la commodité de la description, l'axe des ordonnées détermine une direction qualifiée de « verticale ».
L'équation d'une courbe elliptique définie sur le corps des nombres réels peut être mise sous la forme plus simple (dite équation de Weierstrass) :
- y2 = x3 + ax + b
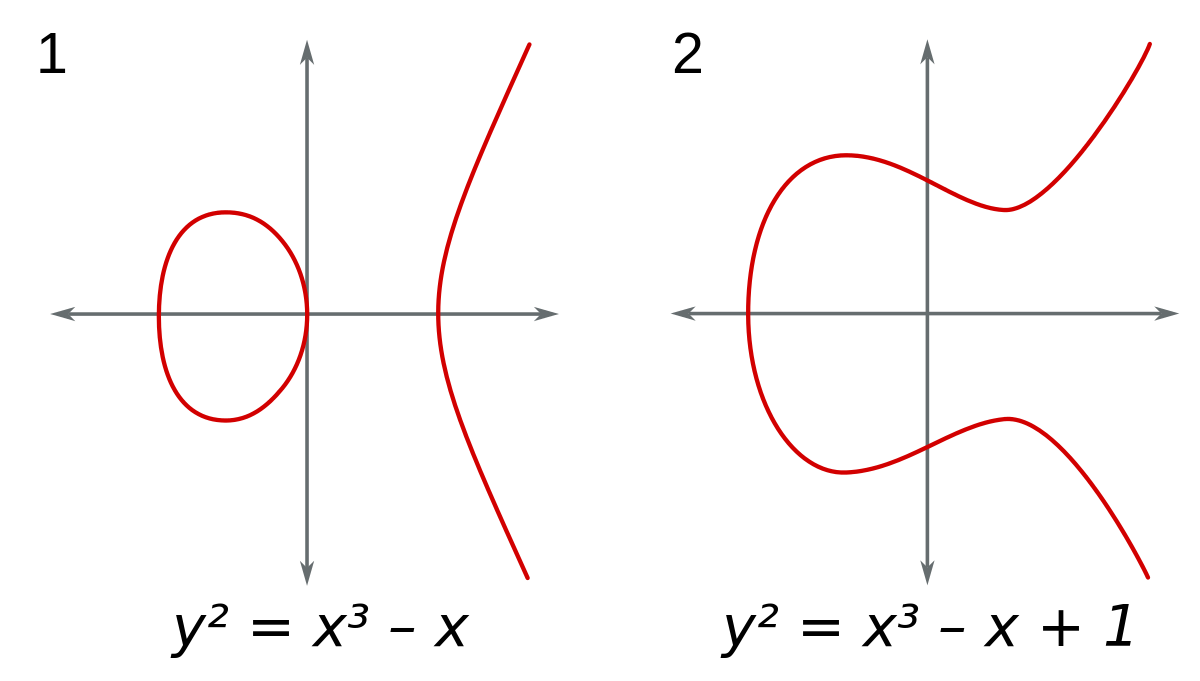
où les coefficients a, b sont des nombres réels. Selon le choix de ces coefficients, les graphes correspondants ont essentiellement deux formes possibles. Voici par exemple les graphes réels associés à deux courbes elliptiques dans le plan affine:
Les points de la courbe sont tous ceux dont les coordonnées (réelles) vérifient l'équation, ainsi qu'un point à l'infini. Comprendre comment et pourquoi ce point doit être pris en compte nécessite de se placer dans le cadre de la géométrie projective, voir section 6 ci-dessous. Ce point à l'infini est essentiel car ce sera l'élément neutre (le 'zéro') pour l'addition des points de la courbe. Intuitivement, il suffit ici de l'imaginer comme le point à l'intersection de toutes les droites verticales.
Les courbes représentées ont une tangente bien définie en chaque point, n'ont ni point double, ni point de rebroussement. Algébriquement, ceci se traduit sur l'équation de la courbe par le fait qu'une certaine combinaison des coefficients
- Δ = − 16(4a3 + 27b2)
ne s'annule pas. La quantité ![]() s'appelle le discriminant de la courbe : un discriminant différent de zéro indique une courbe sans singularités (ou encore courbe non-singulière). Le facteur -16 peut paraître inutile à ce stade mais il intervient dans l'étude plus avancée des courbes elliptiques.
s'appelle le discriminant de la courbe : un discriminant différent de zéro indique une courbe sans singularités (ou encore courbe non-singulière). Le facteur -16 peut paraître inutile à ce stade mais il intervient dans l'étude plus avancée des courbes elliptiques.
Le graphe d'une courbe elliptique peut dès lors prendre deux formes :
- Si le discriminant est positif, il présente deux composantes (comme sur l'image de gauche, où la courbe a un discriminant de 64). Ce cas correspond au fait que le polynôme cubique x3 + ax + b a exactement trois racines réelles distinctes, elles donnent les abscisses des trois points de la courbe elliptique sur l'axe des x.
- Si le discriminant est négatif, il présente une seule composante (comme sur l'image de droite, où la courbe a un discriminant de -368). Ce cas correspond au fait que le polynôme cubique x3 + ax + b a exactement une racine réelle, elle donne l'abscisse du point de la courbe elliptique sur l'axe des x.
Remarque : La courbe d'équation y2 = x3 a pour discriminant 0 : elle a un point de rebroussement à l'origine et ce n'est donc pas une courbe elliptique. Il en est de même pour la courbe d'équation y2 = x3 − 3x + 2, elle aussi de discriminant 0, qui a cette fois un point double en (1,0) ; on remarque que x3 − 3x + 2 = (x − 1)2(x + 2) a une racine multiple. Plus généralement, le polynôme cubique x3 + ax + b a une racine multiple si et seulement si le discriminant Δ est nul; dans ce cas, la courbe correspondante n'est pas elliptique.
Additionner les points : définition par la méthode des tangentes et des sécantes
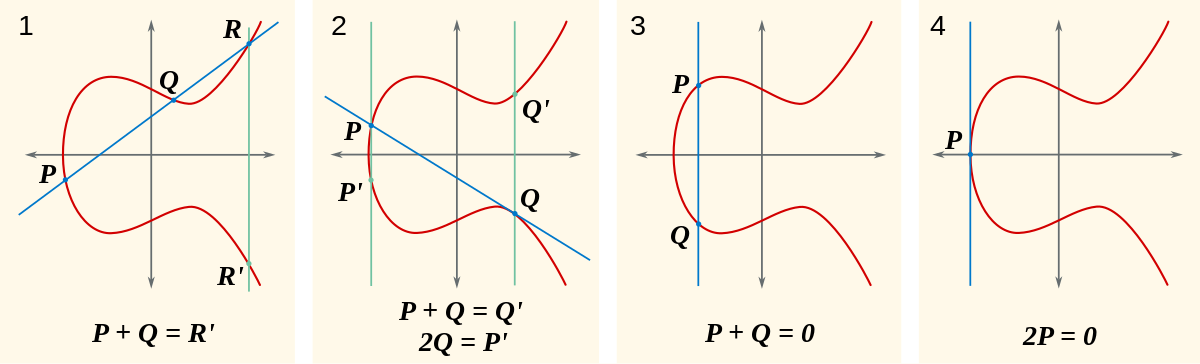
L'addition de deux points sur une courbe elliptique E est rendue possible par la propriété suivante, qui est un cas particulier du Théorème de Bézout sur l'intersection de courbes algébriques sur les réels : une droite sécante passant par deux points de la courbe recoupe la courbe en un troisième point (distinct ou non). On peut s'en convaincre en regardant les figures ci-dessous ou, plus rigoureusement, en lisant la section suivante. Une fois cette propriété admise, on procède ainsi.
Pour définir l'addition de deux points distincts P, Q sur la courbe elliptique E, on remarque d'abord que par ces deux points passe une droite bien définie. À cause de la propriété indiquée, cette droite recoupe donc la courbe E en un troisième point R. Intuitivement, ce point R de la courbe, bien défini à partir des deux points P et Q, serait un bon candidat pour être leur somme. Mais ce choix ne donnerait pas les propriétés qu'on attend d'une bonne addition : par exemple, on ne pourrait pas bien définir le zéro (l'élément neutre additif). On complique donc un peu la construction en prenant comme 'somme' de P et Q le symétrique de ce point R par rapport à l'axe des abscisses. Ceci revient à prendre le point de même abscisse x que R et d'ordonnée opposée à celle de R : à cause de la forme de l'équation de la courbe, ce point appartient bien à la courbe, comme souhaité. On note ce point tout naturellement P + Q. On verra plus loin pourquoi cette notation est justifiée, c'est-à-dire pourquoi la construction faite a toutes les propriétés qu'on attend d'habitude d'une addition.
Il y a quelques cas délicats :
- Si la droite (P Q) est verticale, on considère que le troisième point d'intersection R est le point à l'infini, et qu'il est son propre symétrique par rapport à l'axe des ordonnées. Donc la somme des deux points est le point à l'infini.
- Si la droite (P Q) est la tangente à la courbe en l'un des deux points, on considère que le troisième point d'intersection R est encore le point de tangence, et la somme est donc son symétrique. Cela correspond bien à l'idée intuitive (mais qu'on peut rendre parfaitement rigoureuse) qu'une tangente a un contact double avec la courbe.
- Enfin, pour définir la somme d'un point avec lui-même (P + P ou encore 2P), on utilise encore la tangente au point P = Q. Elle recoupe la courbe en un troisième point (qui peut être d'ailleurs distinct ou non de P) et 2P est le symétrique de ce point.
Voici des illustrations des différents cas possibles.
On voit sur les graphes que la définition donnée est compatible avec le choix du point à l'infini comme 'zéro', élément neutre pour l'addition. Soit P0 ce point à l'infini. Pour trouver P + P0, on doit, selon la méthode décrite, tracer la droite passant par le point P et le point P0 : c'est la verticale passant par P. Elle recoupe justement la courbe elliptique au point P', symétrique de P par rapport à la droite des abscisses ; le point P + P0 cherché, par définition de l'addition, est le symétrique de ce point P', donc c'est P lui-même : on a bien trouvé que P + P0 = P ce qui correspond bien à ce qu'on attend d'un 'zéro' pour l'addition. Dans la suite, ce point sera donc simplement noté 0 ou 0E (pour rappeler qu'il s'agit du zéro pour l'addition sur la courbe E), il ne faut pas le confondre avec le point origine O de coordonnées (0, 0) dans le plan.
Additionner les points : les équations
Cette construction géométrique se traduit aussi par des équations : on peut calculer les coordonnées (xP + Q,yP + Q) du point P + Q en fonction de celles de P = (xP,yP) et de Q = (xQ,yQ). Tous ces points sont sur la courbe elliptique E.
- 1er cas :
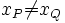 . On pose s = (yP − yQ) / (xP − xQ) et t = (yPxQ − yQxP) / (xP − xQ). La droite qui passe par les points P et Q a pour équation y = sx + t (le nombre s est bien sa pente). On peut calculer l'intersection de cette droite avec E, et on trouve trois solutions : les points P = (xP,yP) et Q = (xQ,yQ), bien sûr, et un troisième point R de coordonnées xR = s2 − xP − xQ, yR = sxR + t. Finalement, le point P + Q (qui est le symétrique de R par rapport à l'axe des abscisses) a pour coordonnées :
. On pose s = (yP − yQ) / (xP − xQ) et t = (yPxQ − yQxP) / (xP − xQ). La droite qui passe par les points P et Q a pour équation y = sx + t (le nombre s est bien sa pente). On peut calculer l'intersection de cette droite avec E, et on trouve trois solutions : les points P = (xP,yP) et Q = (xQ,yQ), bien sûr, et un troisième point R de coordonnées xR = s2 − xP − xQ, yR = sxR + t. Finalement, le point P + Q (qui est le symétrique de R par rapport à l'axe des abscisses) a pour coordonnées :
- xP + Q = xR = s2 − xP − xQ
- yP + Q = − yR = − s(s2 − xP − xQ) + t.
- 2e cas : xP = xQ et
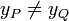 . Dans ce cas, nécessairement yP = − yQ (à cause de l'équation de la courbe). La droite sécante qui joint les deux points est verticale, donc le troisième point d'intersection de cette sécante avec la courbe est le point à l'infini. Le point P + Q est donc le point à l'infini.
. Dans ce cas, nécessairement yP = − yQ (à cause de l'équation de la courbe). La droite sécante qui joint les deux points est verticale, donc le troisième point d'intersection de cette sécante avec la courbe est le point à l'infini. Le point P + Q est donc le point à l'infini.
- 3e cas : xP = xQ et
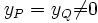 , autrement dit P = Q et ce point n'est pas sur l'axe des abscisses. L'équation de la tangente à la courbe en P est y = sx + t, avec cette fois
, autrement dit P = Q et ce point n'est pas sur l'axe des abscisses. L'équation de la tangente à la courbe en P est y = sx + t, avec cette fois 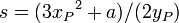 et
et
![]() . Le point P + P (qu'on note naturellement 2P) a donc pour coordonnées :
. Le point P + P (qu'on note naturellement 2P) a donc pour coordonnées :
- x2P = s2 − 2xP
- y2P = − yP + s(xP − x2P).
- 4e cas : xP = xQ et yP = yQ = 0. Le point en question se trouve sur l'axe des abscisses, on voit sur l'équation que la tangente à la courbe passant par ce point est verticale, donc le troisième point d'intersection de cette tangente avec la courbe est le point à l'infini. Le point P + P = 2P est donc le point à l'infini.
Loi de groupe : résumé et justification
On vient donc de définir, géométriquement et sur les coordonnées, une loi de composition sur les points de la courbe E, notée + : autrement dit, on a défini pour tous les points P et Q de la courbe, distincts ou non, le point P + Q. On prend le point à l'infini comme élément neutre (on le note traditionnellement OE). On prend pour opposé d'un point P le symétrique de P par rapport à la droite des abscisses ; on le note − P.
Théorème — L'ensemble des points à coordonnées réelles de la courbe (en incluant le point à l'infini), muni de cette loi de composition, forme un groupe commutatif.
Démonstration :
- Si deux points P et Q sont des points à coordonnées réelles de la courbe ou le point à l'infini, il en est de même de P + Q et de − P : la loi définie est bien une loi de composition interne.
- Le fait que le point à l'infini est élément neutre a été déjà vérifié plus haut. Ceci provient du fait que la droite joignant un point quelconque P au point à l'infini est la droite verticale passant par P, elle recoupe la courbe au point symétrique de P par rapport à l'axe des abscisses; la somme de P et de OE est le symétrique de ce point, donc P lui-même.
- La droite joignant un point quelconque P et son symétrique par rapport à l'axe des abscisses, noté − P, est une droite verticale, le 3e point d'intersection avec la courbe est donc le point à l'infini (qui est son propre symétrique par rapport à l'axe des abscisses), d'où P + ( − P) = OE.
- La commutativité est évidente, car la droite joignant deux points P et Q est aussi ...la droite joignant les points Q et P. Donc P + Q= Q + P.
- La seule propriété difficile est en fait l'associativité, c'est-à-dire que, pour trois points quelconques
On peut démontrer cette associativité directement par le calcul, à l'aide des équations données plus haut.
Une autre démonstration de l'associativité repose sur un résultat de géométrie algébrique, le théorème fondamental de Max Noether. Une conséquence en est le théorème des neuf points : il implique ici, que si la courbe E intersecte deux courbes cubiques C et C' chaque fois en 9 points, et si 8 de ces points sont les mêmes pour C et C', alors le 9e point d'intersection est aussi le même. L'idée de la preuve est de fabriquer les deux cubiques C et C' de manière à contrôler huit de leurs points d'intersection avec la courbe elliptique et à s'arranger pour que le 9e soit l'un des deux points (P + Q) + R ou P + (Q + R) que l'on veut comparer (ou leurs symétriques). On considère donc la droite L1 passant par les points P et Q, la droite M1 passant par les points P + Q et 0E, la droite L2 passant par les points P + Q et R, d'une part, et d'autre part, la droite M2 passant par les points Q et R, la droite L3 passant par les points Q + R et 0E et la droite M3 passant par les points Q + R et P. Le produit des équations des trois droites L1, L2, L3 définit une courbe cubique C, de même le produit des équations des trois droites M1, M2, M3 définit une courbe cubique C'. Les intersections de ces deux cubiques avec la courbe elliptique E sont 9 points, dont 8 sont communs par construction (P, Q, R, OE, P + Q, − (P + Q), Q + R, − (Q + R)). Le 9e point d'intersection de E avec C est le point − ((P + Q) + R), celui de E avec C' est le point − (P + (Q + R)). D'après le théorème cité, ces points sont les mêmes, donc aussi leurs symétriques, d'où l'associativité.
Une troisième démonstration de l'associativité peut encore être donnée dans le cadre de la géométrie algébrique. Reposant cette fois sur le théorème de Riemann-Roch, elle déduit directement les propriétés de l'addition sur la courbe elliptique de celle du groupe de Picard de la courbe.
Points d'ordre fini
- Selon son discriminant, une courbe elliptique a un ou trois points à coordonnées réelles sur l'axe des abscisses, c'est-à-dire tels que y = 0. En ces points, la tangente est verticale (c'est-à-dire ici parallèle à l'axe des ordonnées), son 3e point d'intersection avec la courbe est le point à l'infini. Donc P + P = 2P = 0. On dit qu'un tel point est d'ordre 2. Puisque P = − P, l'ensemble formé d'un tel point et du point à l'infini forme un sous-groupe du groupe des points de la courbe ; il est cyclique d'ordre 2. Si la courbe a trois points d'ordre 2, c'est-à-dire lorsque le discriminant Δ est positif, l'ensemble de ces points forme (avec le point à l'infini) un groupe de cardinal 4, isomorphe à deux copies du groupe cyclique d'ordre 2, c'est-à-dire un groupe de Klein.
- Quant aux points d'ordre 3, ce sont ceux qui vérifient P + P + P = 3P = 0, soit 2P = − P. Autrement dit, la tangente au point P doit recouper la courbe encore une fois au même point. Ceci correspond à un point d'inflexion, où la tangente a un contact d'ordre supérieur à 2 avec la courbe.
- En utilisant par exemple les équations d'une tangente à la courbe données section I.2, on trouve que les abscisses x des points d'inflexion doivent vérifier une équation du 4e degré. Cette équation a 4 racines complexes et à chacune correspondent deux valeurs de y ; mais on peut montrer qu'il y a seulement deux solutions
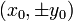 dont les coordonnées sont réelles, soit deux points d'inflexion à distance finie. Le point à l'infini est aussi un point d'inflexion et ces trois points sont alignés. Ils forment un sous-groupe cyclique d'ordre 3.
dont les coordonnées sont réelles, soit deux points d'inflexion à distance finie. Le point à l'infini est aussi un point d'inflexion et ces trois points sont alignés. Ils forment un sous-groupe cyclique d'ordre 3.
- Plus généralement, les points à coordonnées réelles d'ordre n (c'est-à-dire tels que P + P + ... + P = nP = 0) forment un sous-groupe cyclique d'ordre n ou est isomorphe à deux copies du groupe cyclique d'ordre n[réf. souhaitée].