Matrice de rotation - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, et plus précisément en algèbre linéaire, une matrice de rotation est une matrice orthogonale de déterminant 1, ce qui peut s'exprimer par les équations suivantes : ![]() et
et ![]()
![\begin{bmatrix} \cos \theta & -\sin \theta \\[3pt] \sin \theta & \cos \theta \\ \end{bmatrix}](https://static.techno-science.net/illustration/Definitions/autres/4/4597c0562b2c469bb806e1b0c4ac20b2_e83120825a5645efae814662ea1d36e5.png)
Ces matrices sont exactement celles qui, dans un espace euclidien, représentent les isométries (vectorielles) directes. Ces dernières sont aussi appelées rotations vectorielles (d'où le nom de "matrice de rotation"), parce qu'en dimension 2 et 3, elles correspondent respectivement aux rotations affines planes autour de l'origine et aux rotations affines dans l'espace autour d'un axe passant par l'origine.
En dimension 3, ces matrices sont utilisées intensivement pour les calculs de géométrie, de physique et en infographie.
Les matrices de rotation sont toujours carrées et elles sont définies a priori avec des coefficients réels, mais les équations ci-dessus gardent un sens sur n'importe quel corps de coefficients.
L'ensemble de toutes les matrices de rotation de taille fixée forme un groupe appelé groupe des rotations ou groupe spécial orthogonal. C'est un sous-groupe du groupe orthogonal.
Rotations en deux et trois dimensions
Dans toute cette section, on considère que les matrices agissent sur des vecteurs colonne.
En dimension deux
En deux dimensions, les matrices de rotation ont la forme suivante :
![R(\theta) = \begin{bmatrix} \cos \theta & -\sin \theta \\[3pt] \sin \theta & \cos \theta \\ \end{bmatrix}](https://static.techno-science.net/illustration/Definitions/autres/b/b5726960cb1afa1f40c3ca9a2c83aabf_cec3136d921ae9e8cfcf373d218c9fce.png) (rotation d'angle θ)
(rotation d'angle θ)
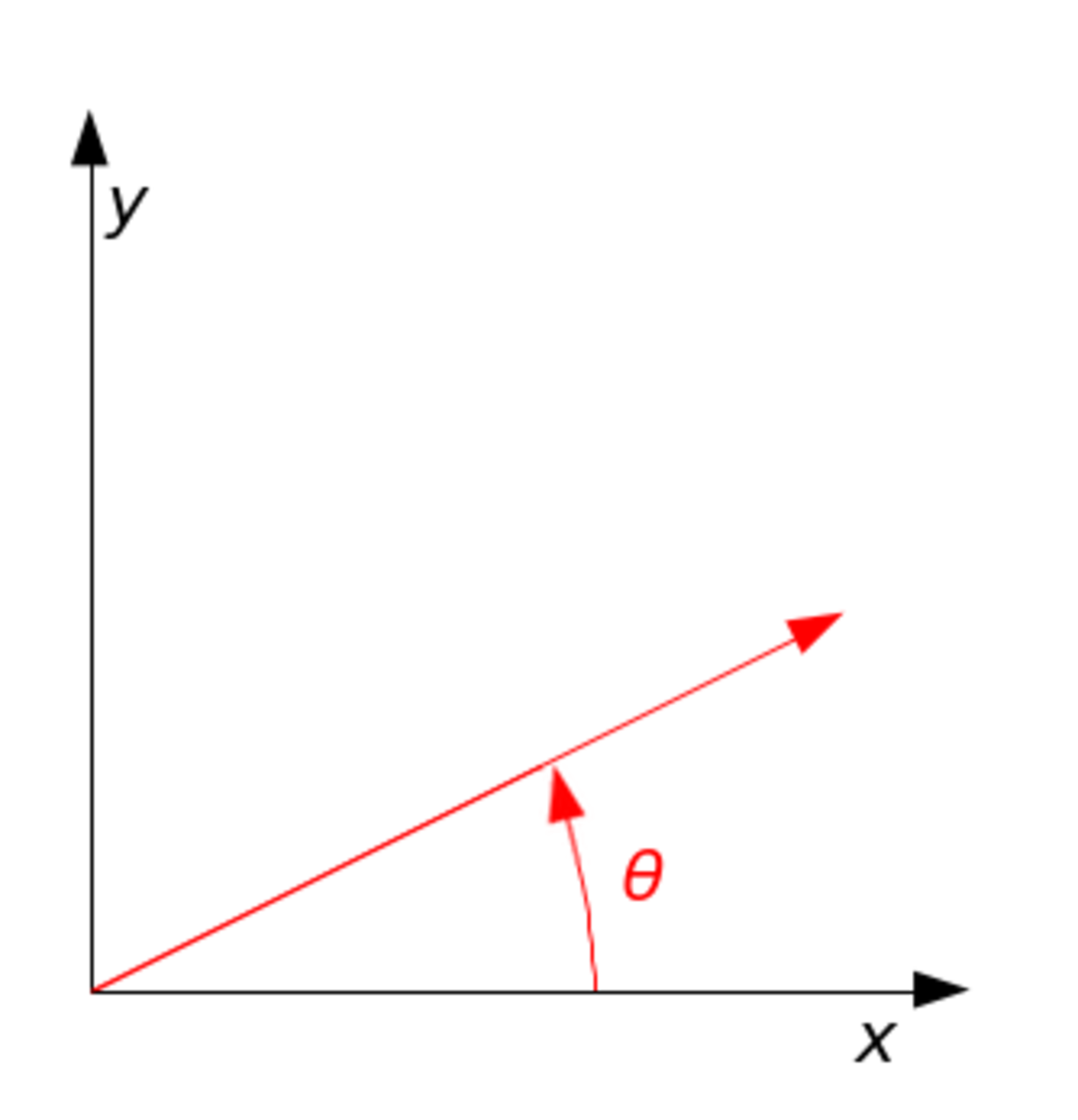
Cette matrice fait tourner le plan d'un angle θ. Elle fait tourner l'axe x en direction de l'axe y.
Dans un plan orienté
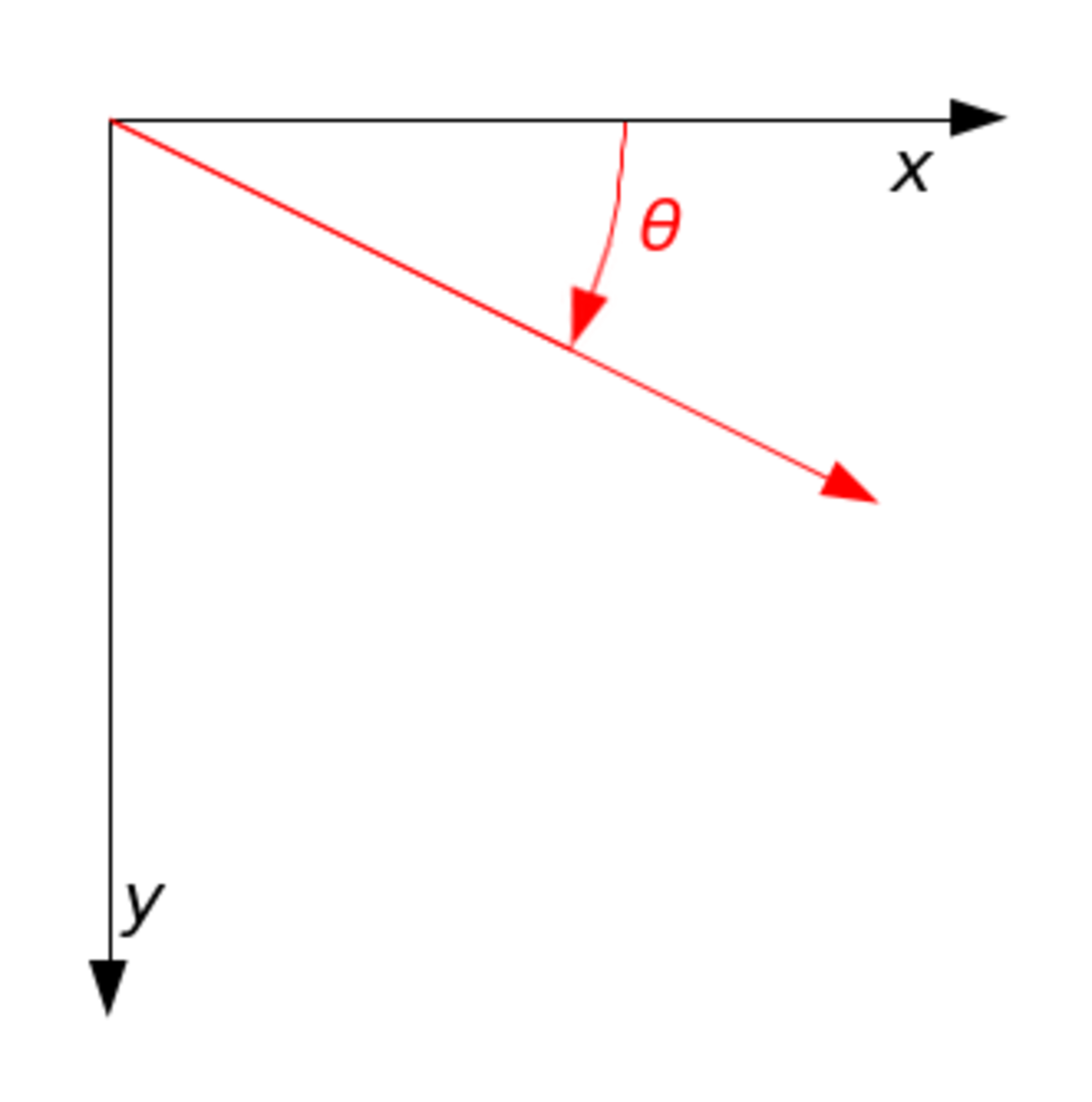
Si l'on a choisi la convention habituelle pour l'orientation du plan (x vers la droite et y vers le haut), cette rotation se fait dans le sens contraire aux aiguilles d'une montre. Si au contraire on a choisi l'orientation inverse (par exemple avec x vers la droite et y vers le bas), cette rotation se fait dans le sens des aiguilles d'une montre. Pour se convaincre qu'il s'agit bien de la même rotation, on n'a qu'à imaginer le plan comme une feuille de papier que l'on regarderait alternativement par au-dessus et par en dessous, par transparence.
En mathématiques et en physique, on se conforme pratiquement toujours à l'orientation usuelle. En revanche, en imagerie numérique, il est fréquent de prendre la convention opposée, qui présente l'avantage d'être compatible avec le sens d'écriture des scripts occidentaux : de gauche à droite et de haut en bas. C'est pour cela que dans de nombreux logiciels, les rotations se font dans le sens des aiguilles d'une montre.
Supposons que l'on adopte l'orientation usuelle du plan. Pour obtenir une rotation dans le sens des aiguilles d'une montre, on remplace simplement θ par –θ :
![R(\theta) = \begin{bmatrix} \cos \theta & -\sin \theta \\[3pt] \sin \theta & \cos \theta \\ \end{bmatrix}](https://static.techno-science.net/illustration/Definitions/autres/b/b5726960cb1afa1f40c3ca9a2c83aabf_cec3136d921ae9e8cfcf373d218c9fce.png) (rotation anti-horaire d'angle θ)
(rotation anti-horaire d'angle θ)
![R(-\theta) = \begin{bmatrix} \cos \theta & \sin \theta \\[3pt] -\sin \theta & \cos \theta \\ \end{bmatrix}](https://static.techno-science.net/illustration/Definitions/autres/0/0237e1fc4ca885136bd1e1288fbe87ee_dc4d89d1346ed29eaf3719bc2a3f2c8a.png) (rotation horaire d'angle θ)
(rotation horaire d'angle θ)
Rotations usuelles
Les matrices correspondant à des rotations de 90° et de 180° sont particulièrement utiles :
![\begin{alignat}{1} R(90^\circ) &= \begin{bmatrix} 0 & -1 \\[3pt] 1 & 0 \\ \end{bmatrix} \end{alignat}](https://static.techno-science.net/illustration/Definitions/autres/2/28c38555c0d496cfc1a19c6681fad4ba_e8a0d447837f87b283bd32d7d207df45.png) (rotation anti-horaire de 90°)
(rotation anti-horaire de 90°)
![\begin{alignat}{1} R(180^\circ) &= \begin{bmatrix} -1 & 0 \\[3pt] 0 & -1 \\ \end{bmatrix} \end{alignat}](https://static.techno-science.net/illustration/Definitions/autres/2/2ad0175c58918f3f2dba42d7d8795bce_5ca29b61198a3790f713165271f6c68c.png) (rotation de 180°)
(rotation de 180°)
![\begin{alignat}{1} R(270^\circ) &= \begin{bmatrix} 0 & 1 \\[3pt] -1 & 0 \\ \end{bmatrix} \end{alignat}](https://static.techno-science.net/illustration/Definitions/autres/0/03a108627dcff6bc1aec1cc4195ba458_00a5f39ebeeb2f29e32b2901c79a7894.png) (rotation horaire de 90°)
(rotation horaire de 90°)
En dimension trois
Les matrices de base
Dans un espace euclidien à 3 dimensions, les matrices de rotations suivantes correspondent à des rotations autour des axes x, y et z (respectivement) :
Les rotations opèrent ainsi : Rx tourne l'axe y vers l'axe z, Ry tourne l'axe z vers l'axe x et Rz tourne l'axe x vers l'axe y.
Dans un espace orienté
Si l'on oriente l'espace en trois dimensions avec les conventions habituelles (x vers l'avant, y vers la droite et z vers le haut), ces rotations se font dans le sens contraire aux aiguilles d'une montre lorsque le troisième axe (celui qui ne subit pas la rotation) est dirigé vers l'observateur. En pratique, pour déterminer le sens de rotation, on peut utiliser la règle de la main droite.
Matrices de rotation dans le cas général
Les autres matrices de rotation s'obtiennent à partir des rotations de base à l'aide de la multiplication de matrices. Par exemple, le produit
représente une rotation dont le lacet, le tangage et le roulis sont respectivement α, β et γ. De la même façon, le produit
représente une rotation dont les angles d'Euler sont α, β et γ (en utilisant la convention z-x-z pour les angles d'Euler).
Axe de rotation
Les rotations en trois dimensions ont un axe, c'est-à-dire une direction laissée inchangée par la rotation.
Axe à partir d'une matrice de rotation
Étant donnée une matrice de rotation R, on peut trouver une matrice colonne u représentant le vecteur dirigeant l'axe en résolvant l'équation :
Matrice de rotation à partir d'un axe et d'un angle
On peut calculer la matrice R de rotation autour d'un axe dirigé par un vecteur unitaire 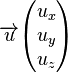 (donc avec
(donc avec ![]() ) et d'un angle θ. La formule est :
) et d'un angle θ. La formule est :
où
Si l'espace en 3 dimensions est orienté de façon conventionnelle, cette rotation se fera dans le sens inverse aux aiguilles d'une montre pour un observateur placé de telle sorte que le vecteur directeur ![]() pointe dans sa direction (règle de la main droite).
pointe dans sa direction (règle de la main droite).
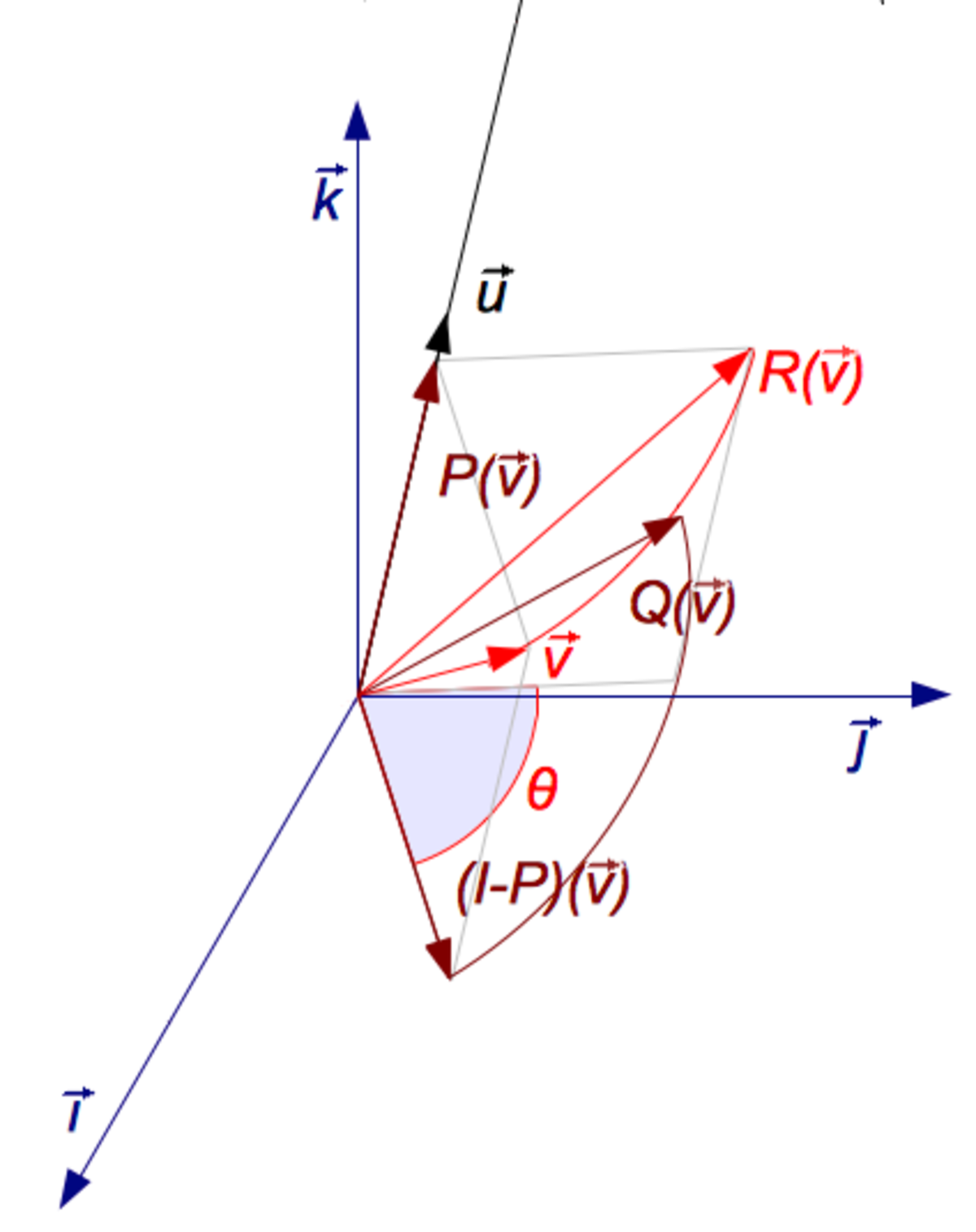
Forme simplifiée de la formule axe-angle
Cette formule peut être simplifiée en
où
I est la matrice identité 3 × 3. La matrice Q est la représentation antisymétrique de ![]() . La matrice P est la projection sur l'axe de rotation et I – P est la projection sur le plan orthogonal à l'axe dirigé par
. La matrice P est la projection sur l'axe de rotation et I – P est la projection sur le plan orthogonal à l'axe dirigé par ![]() .
.
Embûche en dimension supérieure
Ce qui précède peut être généralisé à une dimension n quelconque. L'"axe" de la rotation sera un sous-espace vectoriel de dimension n-2 dont tous les vecteurs sont fixes par la rotation, et pour un tel sous-espace A, les rotations d'"axe" commun A correspondent aux rotation du plan orthogonal à cet axe (et se composent de la même manière).
Mais en dimension supérieure à 3, le fait nouveau est qu'une rotation n'est pas nécessairement de cette forme (i.e. le sous-espace de ses vecteurs fixes peut très bien être de dimension strictement inférieure à n-2) : c'est seulement un produit de rotations de cette forme (cf exemples ci-dessous).
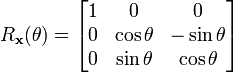
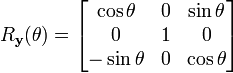

![R = \begin{bmatrix} u_x^2+(1-u_x^2)c & u_x u_y(1-c)-u_zs & u_x u_z(1-c)+u_ys \\[3pt] u_x u_y(1-c)+u_zs & u_y^2+(1-u_y^2)c & u_y u_z(1-c)-u_xs \\[3pt] u_x u_z(1-c)-u_ys & u_y u_z(1-c)+u_xs & u_z^2+(1-u_z^2)c \end{bmatrix}](https://static.techno-science.net/illustration/Definitions/autres/5/51f1345467a490f41539fdedf9c4b8da_2d1d196af8dba1ba141db048de647416.png)
![P = \begin{bmatrix} u_x^2 & u_x u_y & u_x u_z \\[3pt] u_x u_y & u_y^2 & u_y u_z \\[3pt] u_x u_z & u_y u_z & u_z^2 \end{bmatrix} = \textbf{u} \, \textbf{u}^t,\qquad I = \begin{bmatrix} 1 & 0 & 0 \\[3pt] 0 & 1 & 0 \\[3pt] 0 & 0 & 1 \end{bmatrix},\qquad Q = \begin{bmatrix} 0 & -u_z & u_y \\[3pt] u_z & 0 & -u_x \\[3pt] -u_y & u_x & 0 \end{bmatrix}](https://static.techno-science.net/illustration/Definitions/autres/b/b68b5303b31a8ecc22842c8cbf207adb_dae8d93854d4a1bf36e1294e4d94d1b0.png)