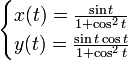Paramétrage - Définition

Introduction

En mathématiques, le paramétrage est un des procédés fondamentaux de définition des courbes, surfaces, et plus généralement des variétés.

C'est ainsi que pour donner corps au concept très général et très vague de courbe, on introduit une notion plus concrète d'arc paramétré. Celle-ci s'inspire directement des problèmes de cinématique.

On étudie par exemple de la succession des points de l'espace occupés par un point animé d'un mouvement dont on connaît la loi en fonction du temps. Ainsi la donnée d'une valeur du temps t permet la détermination de la position M(t) au temps t. En fonction des problèmes étudiés, il sera judicieux de décrire ce même mouvement en changeant de paramètre de référence, en remplaçant par exemple le temps par la distance totale parcourue.

La surface est un objet plus complexe, mais qui peut s'étudier en ayant recours à deux paramètres simultanément : on obtient alors une nappe paramétrée, pour laquelle la donnée de u et de v détermine un point M(u,v). Si on ne fait varier qu'un des deux paramètres, l'autre restant à une valeur fixe, on obtient un arc paramétré. Une nappe paramétrée peut en fait se concevoir comme formée d'une sorte de « grillage » dont les fils sont des arcs paramétrés. Il y a également une notion de changement de paramètre pour les surfaces, mais il faut passer d'un couple (u,v) de paramètres à un autre couple (u',v').

Plus généralement, le nombre de paramètres est lié à la notion de dimension de l'objet géométrique, généralisant le concept de dimension de l'algèbre linéaire. La définition formelle des paramétrages, changements de paramètres, fait intervenir le calcul différentiel.

L'objectif de la géométrie différentielle est de recenser un certain nombre de notions et grandeurs qui sont invariantes par changement de paramètres. Dans le cas d'un arc paramétré, par exemple, on dira qu'une telle notion ou grandeur relève non plus seulement de l'arc paramétré mais d'un objet mathématique nouveau, l'arc (ou la courbe) géométrique.

Les arcs paramétrés

Définition

Un arc paramétré de classe dans l'espace vectoriel E de dimension finie est la donnée

• d'un intervalle I où variera le paramétre réel t
• d'une fonction f de I dans E, de classe

Dans un repère donné de E, la fonction f a des composantes . Par exemple voici un paramétrage du cercle unité du plan (parcouru plusieurs fois) :

.

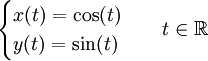Dans la pratique une fonction f peut avoir pour domaine une réunion d'intervalles disjoints ; on étudiera alors séparément chacune des branches correspondantes de la courbe (cf connexité).

En géométrie différentielle on ne considère pas d'arcs qui seraient seulement continus. L'exemple de la courbe de Peano montre que leur comportement peut être très complexe.

Point de paramètre t et point géométrique, multiplicité

Il est tout à fait possible que pour deux valeurs distinctes t et t' on ait f(t)=f(t'). On dira dans ce cas qu'on a affaire à un point multiple de l'arc. Pour gérer ce genre de situation, il convient de distinguer :

• le point de paramètre t, expression qui désigne la donnée conjointe de t et du point f(t) ;
• le point géométrique correspondant qui est un point de E.

La lemniscate de Bernoulli

Ainsi dans le cas d'un point multiple, deux points de paramètres distincts ou plus coïncident avec le même point géométrique. On parle éventuellement de point double, triple, ou de multiplicité k si on connaît le nombre exact de valeurs du paramètre qui donnent ce point géométrique. Si l'arc n'a pas de point multiple (f injective), il est dit simple.

Dans le cas particulier où la fonction est périodique, on dit que la courbe est fermée. On préfèrera alors l'étudier sur une période, et parler de multiplicité des points relativement à une période. Ainsi la lemniscate de Bernoulli :

est fermée (2π périodique) et admet l'origine pour point double (t=0,π). Les courbes fermées ont un certain nombre de propriétés intéressantes détaillées dans l'article correspondant.

Changement de paramètre

On se donne un arc de classe , sous la forme d'un intervalle I et d'une fonction f de I dans E. La trajectoire est l'ensemble f(I) des points géométriques. Mais la même trajectoire peut être parcourue de multiples façons.

Ainsi si est une fonction d'un intervalle J dans I de classe , alors est lui aussi un arc . Pour parcourir la même trajectoire, et passer le même nombre de fois aux mêmes points dans le même ordre, on impose que soit une bijection strictement monotone.

En fait il faut plus : pour assurer la compatibilité avec le calcul différentiel, on dira que g est un paramétrage admissible de l'arc si est un -difféomorphisme. Les deux arcs, avant et après reparamétrage, sont dits -équivalents. On appelle arc géométrique toute classe d'équivalence pour cette relation.

En reprenant le changement de paramétrage , on peut écrire la formule de dérivation des fonctions composées reliant les vecteurs dérivés des deux arcs en deux points correspondants

Les deux vecteurs dérivés sont colinéaires avec un rapport de colinéarité non nul.

Exemples d'invariants

Certaines notions sont inchangées par changement de paramétrage

• la trajectoire : l'ensemble des points parcourus est le même
• la notion de point régulier (vecteur dérivé non nul) : deux points correspondants sont tous les deux réguliers, ou alors tous les deux des points d'arrêt (les dérivées s'annulent).
• la notion de tangente (comme limite de sécantes), ce qui est compatible avec la propriété précédente
• la longueur de l'arc entre deux points d'une part, et deux points correspondants d'autre part.

En conséquence, on dira que ces notions peuvent être étendues à l'arc géométrique.

Mais certaines propriétés font intervenir l'orientation de l'arc, c'est-à-dire le sens de parcours. Dans ce cas il faut distinguer deux types de changements de paramètres

• soit a une dérivée strictement positive en tout point, et on dit qu'il conserve l'orientation.
• soit a une dérivée strictement négative en tout point, et on dit qu'il renverse l'orientation.

Dans le premier cas (respect de l'orientation), le changement de paramétrage conserve d'autres notions

• les demi-tangentes
• l'abscisse curviligne
• les éléments du repère de Frenet et la courbure

On peut définir la notion d'arc géométrique orienté en se limitant à des changements de paramétrages respectant l'orientation.

Paramétrer par l'angle polaire

On se place dans le plan euclidien orienté ramené à un repère orthonormal. Une façon fréquente de définir les courbes est de donner leur équation polaire r fonction de θ : r=h(θ). Il s'agit d'un cas particulier d'arc paramétré puisqu'on peut écrire x(θ)=h(θ).cos(θ),y(θ)=h(θ)sin(θ).

On peut se demander à quelle condition, pour un arc donné, on peut trouver une telle équation polaire. On se contente de traiter le cas des arcs qui ne passent pas par le point O lui-même, car celui-ci apporte des difficultés supplémentaires.

Propriété : passage à une équation «polaire paramétrique»

Si (I,f) définit un arc qui ne passe jamais par O, alors il existe des fonctions r et θ, également , telles que pour tout t, f(t) a pour coordonnées polaires r(t) et θ(t).

Démonstration : par application du théorème de relèvement.

Propriété : condition de passage à une équation «polaire»

Avec les mêmes hypothèses si la fonction θ est un difféomorphisme, on peut prendre θ pour paramètre et obtenir ainsi une véritable équation polaire.