🪢 Esta nova abordagem da teoria das cordas pode finalmente explicar o nosso Universo
As previsões da teoria convencional das cordas são incompatíveis com a observação da energia escura, que parece acelerar a expansão do nosso Universo. Também não se alinham com as teorias viáveis da gravidade quântica, prevendo antes um vasto 'pântano' de universos impossíveis.
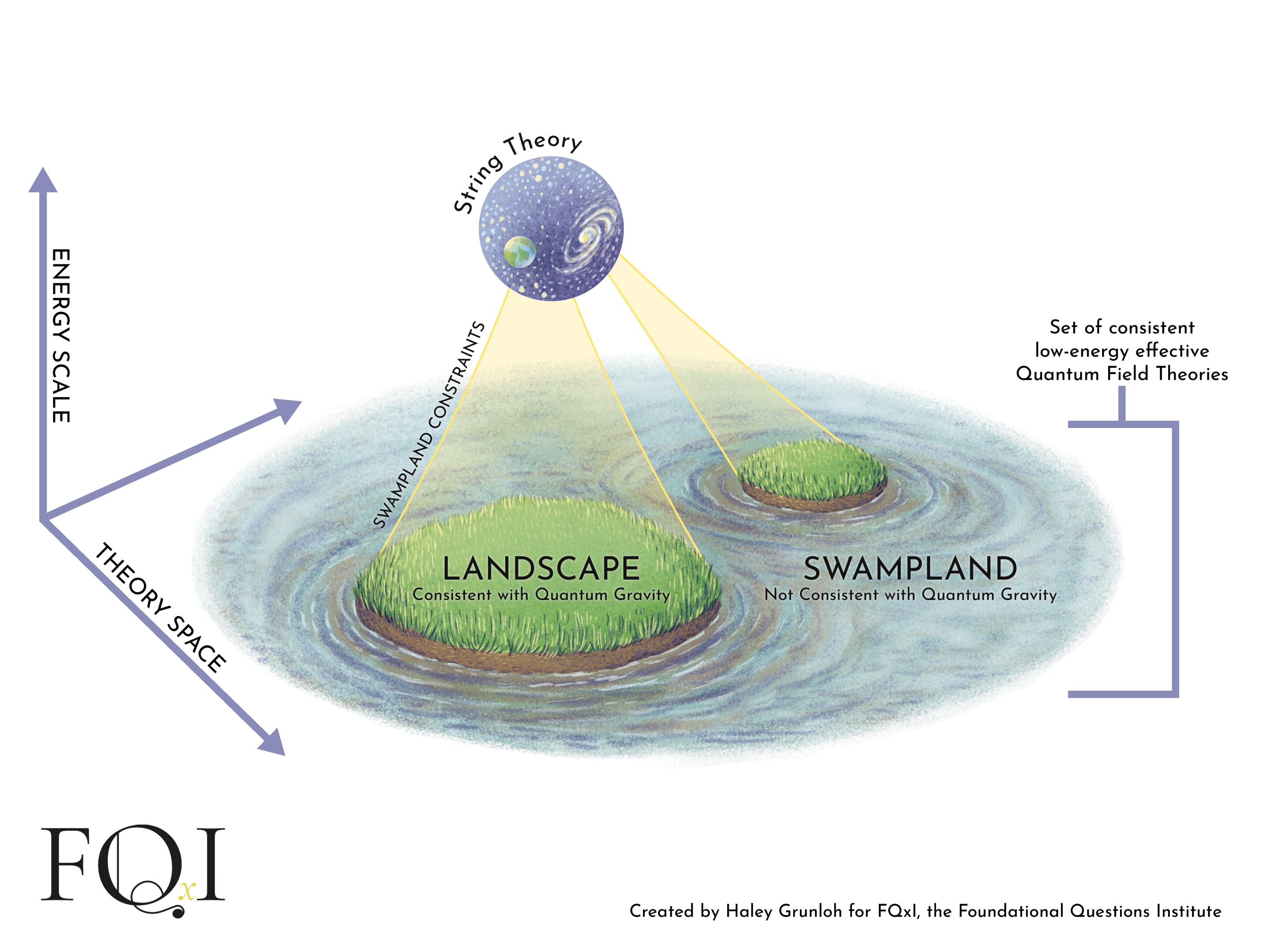
As equações da teoria das cordas dão origem a uma variedade quase infinita de universos potenciais num 'paisagem'. Esta paisagem está rodeada por um 'pântano' de soluções incompatíveis com qualquer teoria viável de gravidade quântica.
Crédito: Criado por Haley Grunloh para o Foundational Questions Institute, FQxI FQxI (2025)
Uma nova análise de Eduardo Guendelman, físico da Universidade Ben-Gurion do Neguev, em Israel, mostra que um subconjunto exótico de modelos de cordas pode oferecer uma saída para este pântano. Nestes modelos, a tensão das cordas é gerada dinamicamente.
Nos anos 2000, os teóricos das cordas perceberam que as equações da teoria não descrevem um único universo, mas um número vertiginoso de 10500 soluções possíveis. Cada uma destas soluções corresponde a um universo com as suas próprias partículas e forças, criando o que se chama a 'paisagem' da teoria das cordas.
Em 2005, descobriu-se que esta paisagem está rodeada por um 'pântano' de soluções que, embora pareçam viáveis, são na realidade incompatíveis com qualquer teoria funcional de gravidade quântica. Para distinguir a paisagem do pântano, foram propostas 'restrições de pântano'.
Guendelman publicou um artigo no The European Physical Journal C mostrando que um certo subconjunto exótico de teorias das cordas pode descrever melhor o nosso universo real. Nestes modelos, a tensão das cordas e a escala de Planck tornam-se dinâmicas, enfraquecendo as restrições do pântano.
O que é a teoria das cordas?
A teoria das cordas é uma abordagem teórica em física que tenta descrever as partículas elementares como minúsculas cordas vibrantes. Estas cordas podem vibrar em diferentes frequências, cada frequência correspondendo a uma partícula diferente.
Esta teoria visa unificar as quatro forças fundamentais da natureza: a gravidade, o eletromagnetismo, a força nuclear forte e a força nuclear fraca. Promete uma descrição coerente do Universo tanto à escala quântica como cosmológica.
No entanto, a teoria das cordas exige a existência de dimensões espaciais adicionais, além das três que conhecemos. Estas dimensões adicionais estão compactificadas, ou seja, enroladas sobre si mesmas em escalas tão pequenas que escapam à nossa perceção direta.
Apesar da sua elegância matemática, a teoria das cordas ainda não foi confirmada por provas experimentais. Permanece assim como uma das abordagens mais promissoras, mas também uma das mais especulativas, da física teórica.
Por que é que a energia escura representa um problema para a teoria das cordas?
A energia escura é uma forma de energia hipotética que explicaria a aceleração da expansão do Universo. A sua existência é deduzida a partir de observações astronómicas, mas a sua natureza exata permanece um mistério.
No âmbito da teoria convencional das cordas, a energia escura representa um problema porque parece incompatível com as 'restrições de pântano'. Estas restrições limitam os tipos de universos que a teoria pode descrever de forma coerente com a gravidade quântica.
Os modelos convencionais da teoria das cordas preveem que a energia escura deveria ser muito mais fraca do que o que é observado, ou mesmo inexistente. Isto coloca o nosso Universo no 'pântano' das soluções teoricamente impossíveis.
Os trabalhos de Guendelman sugerem que modelos com uma tensão dinâmica das cordas podem contornar este problema. Ao tornar a escala de Planck dinâmica, estes modelos enfraquecem as restrições e abrem caminho para uma descrição coerente da energia escura.