Restez toujours informé: suivez-nous sur Google Actualités (icone ☆)
La question posée par Dudeney concernait la transformation d'un triangle équilatéral en un carré par découpage et réarrangement des pièces. Ce type de problème, connu sous le nom de dissection géométrique, intéresse autant les amateurs de puzzles que les scientifiques. La solution originale nécessitait quatre pièces, mais personne n'avait jusqu'ici prouvé qu'il était impossible de faire mieux.
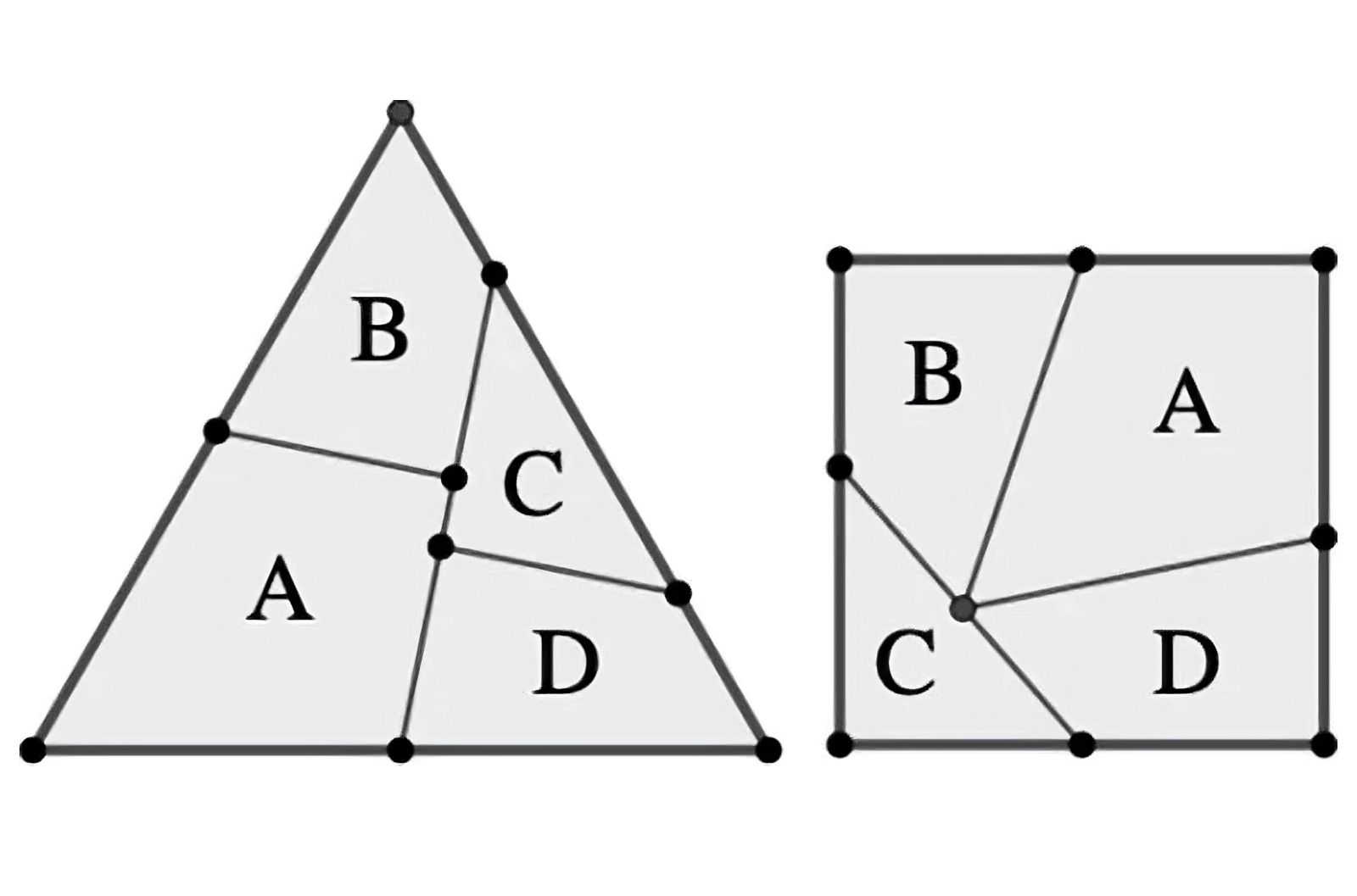
Illustration de la dissection d'un triangle équilatéral en un carré selon la méthode de Dudeney.
Crédit: Erik D. Demaine, Tonan Kamata, Ryuhei Uehara
Une équipe internationale a récemment démontré que quatre pièces étaient bien le minimum nécessaire. Leurs travaux, publiés sur arXiv, s'appuient sur une méthode innovante utilisant des diagrammes de correspondance. Cette approche permet d'analyser les relations entre les bords et les sommets des pièces découpées.
Les chercheurs ont d'abord écarté la possibilité d'une solution en deux pièces, puis ont exploré systématiquement toutes les configurations possibles avec trois pièces. Leur conclusion est sans appel: aucune de ces configurations ne permet d'aboutir à un carré parfait. Cette preuve marque une avancée significative dans la compréhension des problèmes de dissection.
Les applications de ces recherches dépassent le cadre des mathématiques pures. Elles trouvent des échos dans des domaines comme la conception de textiles ou la fabrication de matériaux. La méthode développée par les scientifiques pourrait également ouvrir la voie à la résolution d'autres problèmes de dissection encore non résolus.
L'étude souligne l'importance des diagrammes de correspondance dans l'analyse des dissections. Ces outils graphiques permettent de visualiser les contraintes géométriques et de prouver l'optimalité d'une solution. Ils offrent ainsi une nouvelle perspective sur des problèmes qui font plancher les mathématiciens depuis des siècles.
Cette découverte ne clôt pas seulement un chapitre de l'histoire des mathématiques. Elle pose les bases pour des recherches futures, notamment dans l'optimisation des processus de découpe et d'assemblage. Les scientifiques envisagent déjà d'appliquer leur méthode à d'autres formes géométriques, promettant de nouvelles avancées dans ce domaine.
Qu'est-ce qu'une dissection géométrique ?
Une dissection géométrique consiste à découper une forme en plusieurs pièces qui peuvent être réarrangées pour former une autre forme. Ce concept, qui remonte à l'Antiquité, est à la fois un jeu mathématique et un outil pour résoudre des problèmes pratiques.
Les dissections les plus simples concernent des polygones comme les triangles et les carrés. L'objectif est souvent de minimiser le nombre de pièces nécessaires pour passer d'une forme à l'autre. Cela requiert une compréhension profonde des propriétés géométriques des formes impliquées.
Au-delà des puzzles, les dissections géométriques ont des applications concrètes. Elles sont utilisées dans la conception de motifs pour les textiles, la découpe de matériaux dans l'industrie, et même dans l'art. Leur étude permet d'optimiser l'utilisation des ressources et de réduire les déchets.
La preuve de l'optimalité d'une solution, comme celle de Dudeney, est une étape cruciale. Elle permet de savoir qu'on a atteint la solution la plus efficace possible, ce qui est essentiel pour les applications pratiques.
Comment fonctionnent les diagrammes de correspondance ?
Les diagrammes de correspondance sont des outils graphiques utilisés pour analyser les dissections géométriques. Ils représentent les relations entre les bords et les sommets des pièces découpées, sous forme de graphes.
Dans le cas de la dissection d'un triangle en carré, ces diagrammes permettent de visualiser comment les pièces s'emboîtent. Ils aident à identifier les contraintes géométriques qui rendent certaines configurations impossibles.
Cette méthode est particulièrement utile pour prouver l'optimalité d'une solution. En montrant qu'aucune configuration avec moins de pièces ne satisfait les contraintes, les chercheurs peuvent affirmer que la solution est la meilleure possible.
Les diagrammes de correspondance ouvrent de nouvelles perspectives pour résoudre des problèmes de dissection plus complexes. Leur application pourrait s'étendre à d'autres domaines, comme la conception de structures en ingénierie ou l'optimisation de processus industriels.