💥 Was wäre, wenn ein Universum vor dem Urknall existiert hätte... die Antwort in Simulationen?
Ein britisches Forscherteam schlägt nun einen innovativen Ansatz vor, um diese unbekannten Gebiete zu erkunden. Ihre in Living Reviews in Relativity veröffentlichte Arbeit schlägt vor, fortschrittliche numerische Simulationen zu verwenden, um Einsteins Gleichungen in Umgebungen zu lösen, in denen die Gravitation so intensiv wird, dass sie unsere traditionellen Rechenfähigkeiten übersteigt. Diese Methode, genannt numerische Relativitätstheorie, ermöglicht die Untersuchung kosmologischer Szenarien, die bisher unerreichbar waren.
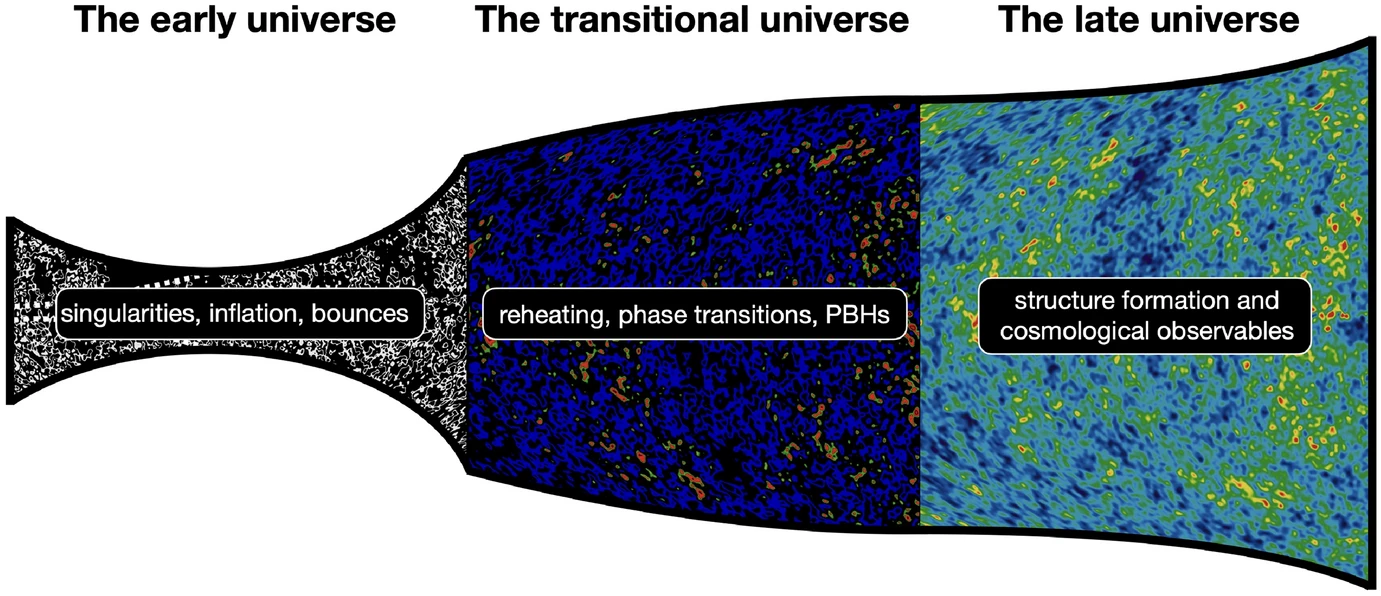
Die Analyse gliedert sich in zwei Teile: die Phase vor dem Urknall, die den Zeitraum bis zum Ende der Inflation in diesem Diagramm abdeckt. Die Phase nach dem Urknall umfasst die nicht-störungstheoretische Dynamik vom Ende der Inflation bis zur Emission der Hintergrundstrahlung (CMB). Die späte Phase des Universums entspricht dem Rest des Diagramms, der die standardmäßige kosmologische Geschichte enthält.
Die numerische Relativitätstheorie ist keine neue Idee: Sie entstand in den 1960er Jahren, um Kollisionen Schwarzer Löcher und Gravitationswellen zu untersuchen. Ihre Anwendung auf die Kosmologie stellt jedoch einen bedeutenden Schritt nach vorne dar. Indem sie die vereinfachende Annahme eines homogenen und isotropen Universums aufgeben, können Forscher verschiedene Anfangsbedingungen modellieren und Theorien wie die kosmische Inflation oder zyklische Universen testen.
Zu den vielversprechenden Anwendungen gehört die Suche nach kosmischen Strings, hypothetischen Strukturen, die nachweisbare Signaturen in der kosmischen Hintergrundstrahlung hinterlassen könnten. Ebenso könnte dieser Ansatz Spuren von Kollisionen zwischen unserem Universum und anderen enthüllen und damit greifbare Beweise für die Theorie der Multiversen liefern. Die Simulationen erfordern eine enorme Rechenleistung, aber technologische Fortschritte machen diese Erkundungen immer realisierbarer.
Die Implikationen dieser Arbeit sind tiefgreifend. Sie könnten nicht nur die Momente nach dem Urknall beleuchten, sondern uns auch Aufschluss darüber geben, was davor existiert haben könnte. Die Idee eines zyklischen Universums, das Expansion und Kontraktion abwechselt, wird so der numerischen Analyse zugänglich. Diese Methodik ebnet den Weg für eine fruchtbare Zusammenarbeit zwischen Kosmologen und Spezialisten für numerische Relativitätstheorie.

Computationale Methoden könnten kosmische Geheimnisse lüften.
Bildnachweis: Gabriel Fitzpatrick für FQxI, FQxI (2025)
Dieser Ansatz stellt einen Paradigmenwechsel in unserer Suche nach den kosmischen Ursprüngen dar. Indem Wissenschaftler die Leistung von Supercomputern mit den Gleichungen der allgemeinen Relativitätstheorie kombinieren, hoffen sie, einige der bestgehüteten Geheimnisse des Universums zu entschlüsseln und philosophische Fragen in durch Simulation lösbare physikalische Probleme zu verwandeln.
Numerische Relativitätstheorie: Wenn Computer das Universum erforschen
Die numerische Relativitätstheorie ist eine Disziplin an der Schnittstelle zwischen theoretischer Physik und Informatik. Sie besteht darin, die Gleichungen von Einsteins allgemeiner Relativitätstheorie mit numerischen statt analytischen Methoden zu lösen. Diese Gleichungen beschreiben, wie Materie und Energie die Raumzeit krümmen und das erzeugen, was wir als Schwerkraft wahrnehmen.
Im Gegensatz zu exakten Lösungen, die oft unrealistische Vereinfachungen erfordern, ermöglichen numerische Methoden die Behandlung extremer physikalischer Situationen. Sie unterteilen das Problem in kleine, einzeln berechenbare Elemente und setzen dann das Gesamtbild wieder zusammen. Dieser Ansatz ist besonders nützlich für die Untersuchung von Singularitäten, jenen Punkten, an denen physikalische Größen unendlich werden.
Die Entwicklung dieser Disziplin wurde durch konkrete Probleme wie die Vorhersage von Gravitationswellen bei Kollisionen kompakter Objekte motiviert. Heute findet sie Anwendungen in der Kosmologie, um die Entwicklung des Universums mit verschiedenen Anfangsbedingungen zu simulieren. Jüngste Fortschritte in der Rechenleistung eröffnen noch ambitioniertere Perspektiven.
Die technischen Herausforderungen bleiben bedeutend, insbesondere das Management numerischer Instabilitäten und die Notwendigkeit, Ergebnisse durch unabhängige Methoden zu validieren. Trotz dieser Schwierigkeiten etabliert sich die numerische Relativitätstheorie als unverzichtbares Werkzeug zur Erforschung der Grenzen unseres kosmologischen Wissens.
Kosmische Inflation: Der Atem des Universums
Die kosmische Inflation ist eine bedeutende Theorie in der Kosmologie, die eine exponentielle Expansion des Universums in den ersten Augenblicken nach dem Urknall postuliert. In einem winzigen Sekundenbruchteil hätte sich das Universum um einen beträchtlichen Faktor ausgedehnt, seine Struktur homogenisiert und die großen Strukturen hervorgebracht, die wir heute beobachten.
Diese Phase ultra-schneller Expansion löst mehrere kosmologische Probleme, wie die Homogenität der kosmischen Hintergrundstrahlung im großen Maßstab. Sie erklärt auch, warum das Universum im großen Maßstab flach erscheint und warum wir keine magnetischen Monopole beobachten, Teilchen, die von einigen Theorien vorhergesagt, aber nie nachgewiesen wurden.
Der genaue Mechanismus der Inflation bleibt jedoch wenig verstanden. Physiker vermuten, dass sie durch ein Skalarfeld ausgelöst worden sein könnte, eine Art Energie im Quantenvakuum. Der Übergang zwischen der inflationären Phase und der standardmäßigen Expansion des Universums stellt ein weiteres aktives Forschungsgebiet dar.
Beobachtungen der kosmischen Hintergrundstrahlung, insbesondere durch die Missionen Planck und WMAP, haben indirekte Beweise für die Inflation geliefert. Die direkte Detektion primordialer Gravitationswellen, die als direkte Signatur der Inflation gilt, bleibt jedoch ein unerreichtes Ziel, das viele Beobachtungsprojekte motiviert.