End of the irrational: mathematician solves 200-year-old problem 📐
Published by Cédric,
Article author: Cédric DEPOND
Source: The American Mathematical Monthly
Other Languages: FR, DE, ES, PT
Article author: Cédric DEPOND
Source: The American Mathematical Monthly
Other Languages: FR, DE, ES, PT
Follow us on Google News (click on ☆)
This breakthrough, published in The American Mathematical Monthly, challenges algebraic principles established since the 19th century. By relying on combinatorial sequences, it opens unexpected perspectives for pure and applied mathematics.
The historical deadlock of high-degree polynomials
Polynomial equations like x² + 5x + 6 = 0 have been solved since antiquity. And they are found everywhere, from orbit calculations to weather forecasting and computer cryptography! However, starting from degree five (beyond x⁴), they became unsolvable because they require numbers like √2 or π, whose decimals never terminate. Évariste Galois demonstrated in 1832 the impossibility of a general solution by radicals, forcing mathematicians to rely on numerical approximations.
Norman Wildberger from the University of New South Wales rejects this limitation. According to him, the use of irrational numbers like √2 or π introduces artificial complexities. These numbers, requiring infinite decimals, are in his view "incalculable in practice." His solution? Ignore them.
Indeed, his method avoids these pitfalls by using power series, polynomial extensions with potentially infinite terms. Tested on a historic cubic equation, it provided precise results without resorting to radicals.
The key: geodesic numbers
The innovation relies on a generalization of Catalan numbers, a combinatorial sequence that indicates how to divide a polygon into triangles. Wildberger and his colleague Dean Rubine extended this logic to higher dimensions, creating a structure named Geode.
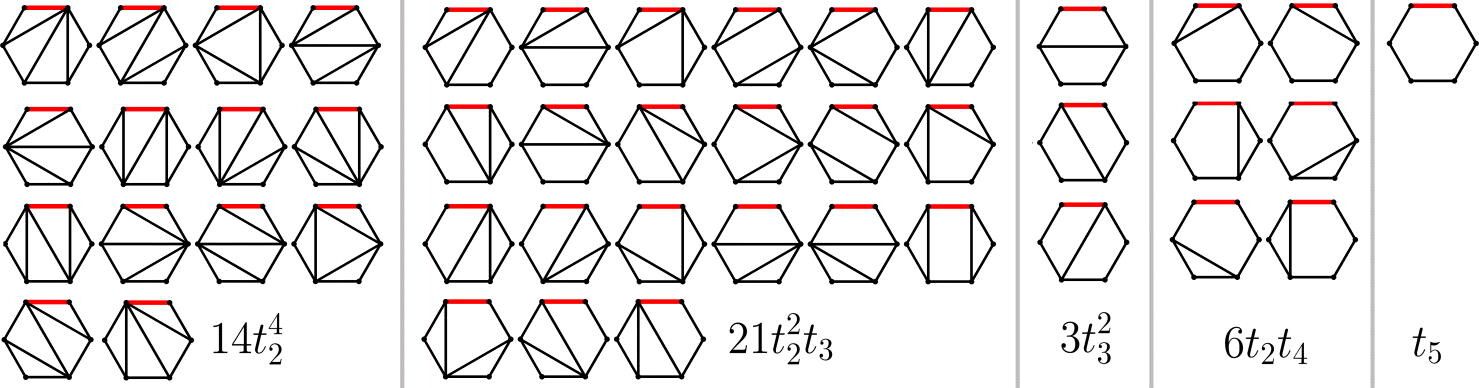
Representation with Geode.
These new numbers allow solving complex equations by exploiting multidimensional geometric patterns. Their purely algebraic approach bypasses traditional approximations. It could optimize algorithms in computer science or biological modeling.
Result? Even x⁵ becomes solvable! Tested on a 17th-century equation, his technique yielded precise results... without ever using infinite numbers. Geode also offers an unexplored research field. Concrete applications are conceivable, such as improving orbital calculations or data compression.