Quantum physics "accidentally" unveils a new representation of π (Pi)
Follow us on Google News (click on ☆)

Pi contains an infinite number of non-repeating decimals.
Illustrative image from Pixabay
Under certain conditions, this new formula for π approximates that of Madhava, a 15th-century Indian mathematician, who was the first to propose a series for π. Researchers Arnab Saha and Aninda Sinha from the Centre for High Energy Physics (CHEP) published their findings in Physical Review Letters.
Initially, Saha and Sinha did not aim to discover a new representation of π. Their research was focused on studying high-energy particle interactions, such as those observed at the Large Hadron Collider, within the framework of string theory. This theory suggests that quantum processes result from string vibrations.
The team combined two mathematical tools: Euler's Beta function and the Feynman diagram. Euler's Beta function is used in various fields of physics and engineering, while the Feynman diagram describes the energy exchanges during particle interactions.
Their approach not only effectively modeled particle interactions but also led to the discovery of a new series to represent π. In mathematics, a series allows for the decomposition of a parameter like π into its components. The new series quickly approximates the value of π, which is essential for high-energy particle scattering calculations.
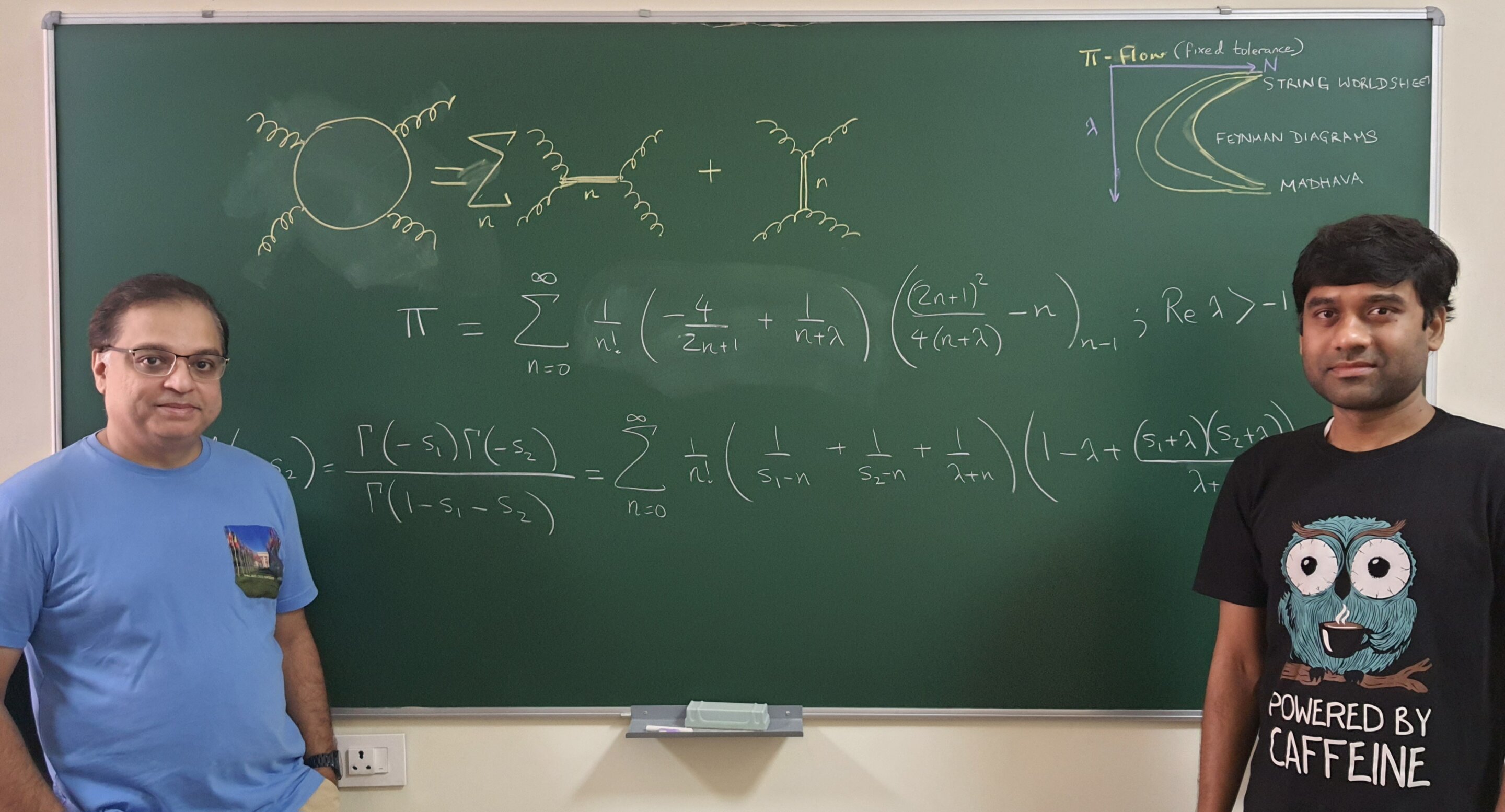
Aninda Sinha (left) and Arnab Saha (right).
Credit: Manu Y
The researchers explain that this result was possible thanks to modern mathematical tools that were not available during the first modeling attempts in the 1970s. Although these works remain theoretical, they could eventually lead to practical applications, similar to Paul Dirac's discoveries about electrons that led to advanced medical technologies.
Sinha concludes by emphasizing that this research, although it may seem far removed from daily concerns, offers the pure pleasure of theory for theory's sake.