La physique quantique fait émerger "par accident" une nouvelle représentation de π (Pi)
Restez toujours informé: suivez-nous sur Google Actualités (icone ☆)

Pi possède un nombre infini de décimales non répétitives.
Image d'illustration Pixabay
Sous certaines conditions, cette nouvelle formule pour π se rapproche de celle de Madhava, mathématicien indien du XVe siècle, qui fut le premier à proposer une série pour π. Les chercheurs Arnab Saha et Aninda Sinha, du Centre de Physique des Hautes Énergies (CHEP), ont publié leurs travaux dans Physical Review Letters.
Initialement, Saha et Sinha n'avaient pas pour objectif de trouver une nouvelle représentation de π. Leur recherche se concentrait sur l'étude des interactions de particules à haute énergie, telles que celles observées au Large Hadron Collider, dans le cadre de la théorie des cordes. Cette théorie suppose que les processus quantiques résultent des vibrations de cordes.
L'équipe a combiné deux outils mathématiques: la fonction Beta d'Euler et le diagramme de Feynman. La fonction Beta d'Euler intervient dans divers domaines de la physique et du génie, tandis que le diagramme de Feynman décrit les échanges d'énergie lors de l'interaction de particules.
Leur approche a permis non seulement de modéliser efficacement les interactions de particules, mais aussi de découvrir une nouvelle série pour représenter π. En mathématiques, une série permet de décomposer un paramètre comme π en ses composants. La nouvelle série permet d'approcher rapidement la valeur de π, essentielle pour les calculs de diffusion de particules à haute énergie.
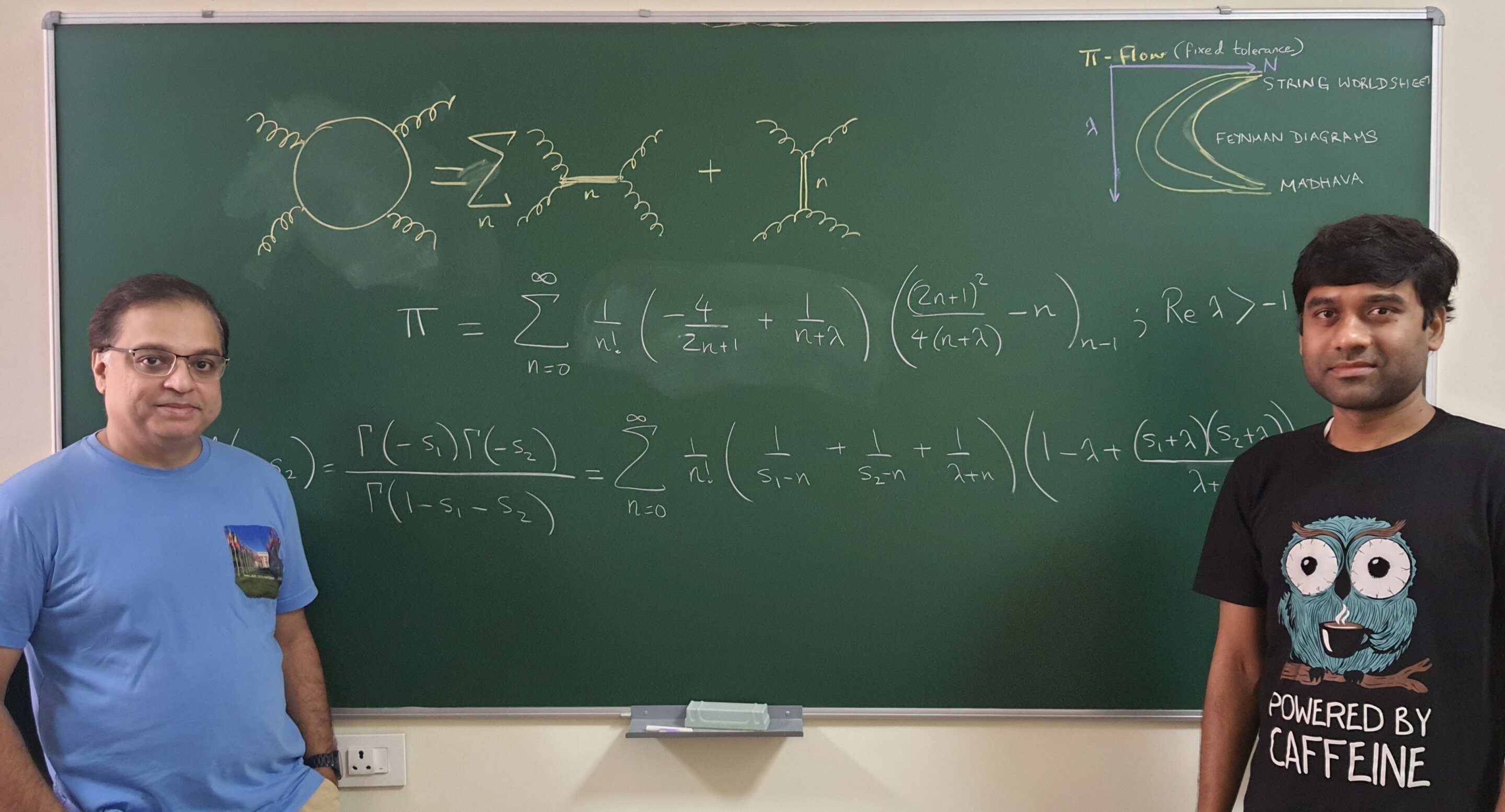
Aninda Sinha (gauche) et Arnab Saha (droite).
Crédit: Manu Y
Les chercheurs expliquent que ce résultat a été possible grâce à des outils mathématiques modernes, absents lors des premières tentatives de modélisation dans les années 1970. Bien que ces travaux restent théoriques, ils pourraient, à terme, aboutir à des applications pratiques, à l'instar des découvertes de Paul Dirac sur les électrons qui ont conduit à des technologies médicales avancées.
Sinha conclut en soulignant que cette recherche, bien qu'elle puisse sembler éloignée des préoccupations quotidiennes, offre le plaisir pur de la théorie pour la théorie.