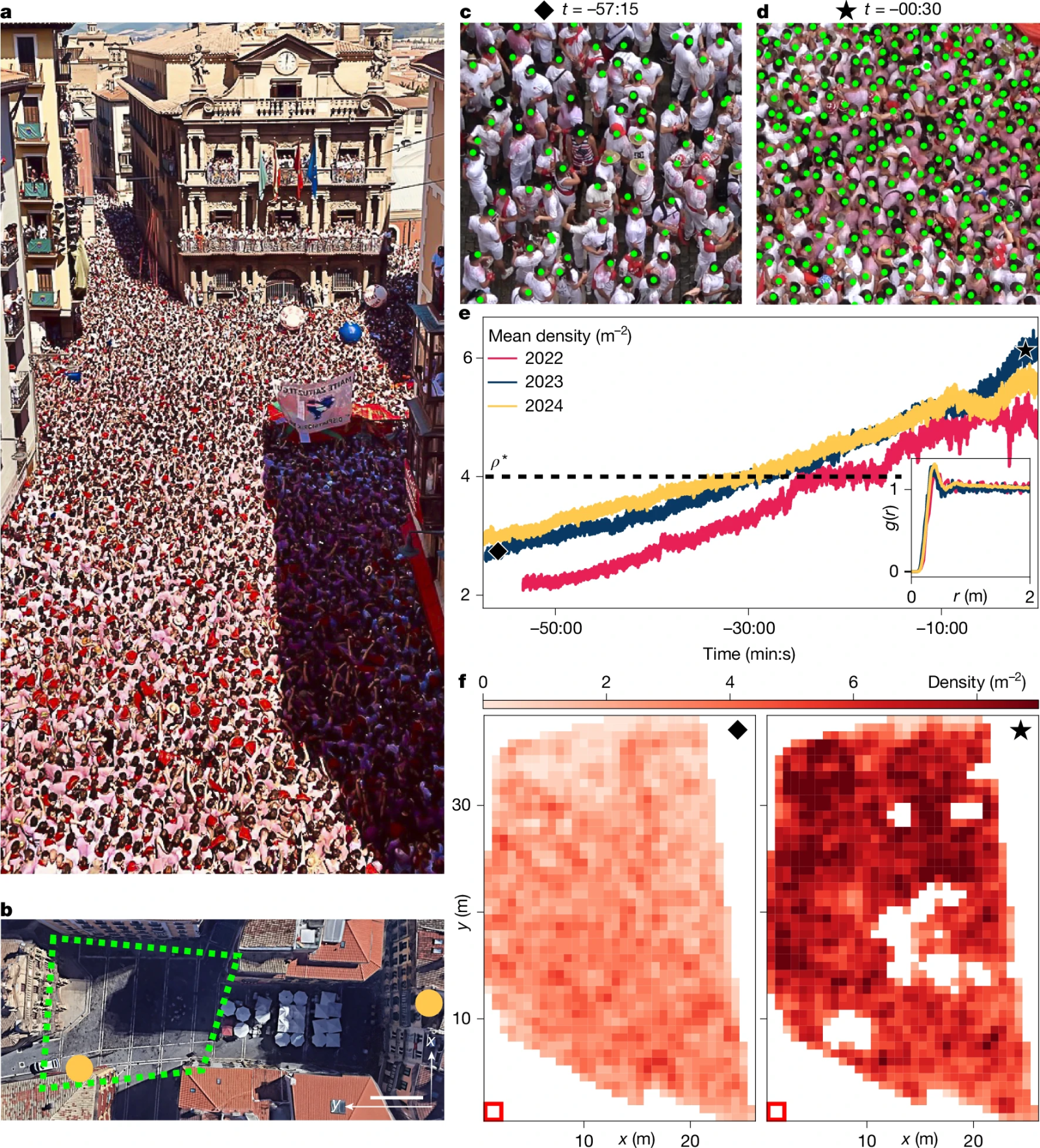
a) Foto der Menschenmenge während der Eröffnungszeremonie des San-Fermín-Festivals (2019).
b) Luftaufnahme der Plaza Consistorial mit dem analysierten Bereich (gestricheltes Polygon) und den Beobachtungspunkten (orangefarbene Punkte). Maßstab: 10 m.
c) Nahaufnahme der Menschenmenge 57 Minuten und 15 Sekunden vor Beginn des Festivals mit der Position der Köpfe der Teilnehmer (grüne Punkte).
d) Nahaufnahme 30 Sekunden vor Beginn des Festivals, die eine deutlich erhöhte Dichte zeigt.
e) Durchschnittliche Dichte der Menschenmenge in Abhängigkeit von der Zeit vor Beginn. Die Raute zeigt t = −57:15 (siehe c) und der Stern t = −00:30 (siehe d). Die Dichte nimmt langsam und stetig zu. Der Kasten zeigt die radiale Verteilungsfunktion g(r).
f) Lokale Dichtekarten bei t = −57:15 (links) und t = −00:30 (rechts). Die weißen Bereiche zeigen verdeckte Sichtfelder.
Dichte Menschenmengen gehören zweifellos zu den gefährlichsten Umgebungen unserer modernen Gesellschaft. Die kollektiven Bewegungen, die in ihnen entstehen, können tatsächlich zu unkontrollierten Verlagerungen von Personengruppen mit einer Gesamtmasse von mehreren Tonnen führen und in den tragischsten Situationen zu erheblichen Verlusten durch Gedränge und Erstickung.
Die Modellierung der Dynamik von Menschenmengen stützt sich jedoch hauptsächlich auf Modelle von interagierenden Individuen, die zwar effektiv für die Beschreibung kleiner Gruppen sind, aber Schwierigkeiten haben, das komplexe Verhalten von sehr dichten Menschenmengen mit Tausenden von Personen zu erklären.
In einer aktuellen Studie haben Forscher der ENS Lyon, der Universität Lyon 1 und der Universität Navarra (Spanien) die Bewegungen von Tausenden von Menschen auf der Plaza Consistorial in Pamplona (Spanien) während der Eröffnungszeremonie der San-Fermín-Feste analysiert. Sie entdeckten, dass sich in beengten Räumen dichte Menschenmengen zu riesigen Oszillatoren selbst organisieren können.
Ohne äußere Anregung koordinieren Tausende von Individuen spontan ihre Bewegungen, um kreisförmigen Bahnen mit einer bestimmten Periodizität zu folgen. Auf der Grundlage dieser Beobachtungen und grundlegender physikalischer Prinzipien entwickelten die Autoren ein mechanisches Modell, das die Entstehung dieser kollektiven Bewegungen erklärt.
Dieses Modell zeigt, dass extrem spezifische Reibungskräfte (sogenannte ungerade Kräfte) bei hoher Dichte einen kollektiven Phasenübergang induzieren, der zu chiralen Schwingungen führt: Sehr große Teile der Menge beginnen kohärent in eine zufällige Richtung mit einer charakteristischen Periode von 20 Sekunden zu rotieren.
Diese Ergebnisse erklären nicht nur die experimentellen Beobachtungen, sondern auch die Tatsache, dass ähnliche Dynamiken bei katastrophalen Ereignissen wie der Love Parade in Duisburg (Deutschland) im Jahr 2010 zu beobachten waren, bei der 21 Menschen ums Leben kamen.

Bild der Plaza Consistorial in Pamplona (Spanien). Jedes Jahr versammeln sich am 6. Juli um 12:00 Uhr mehr als fünftausend Menschen, um die Eröffnung des San-Fermín-Festivals zu feiern.
© Bartolo Lab, ENS de Lyon.
Die Robustheit der in dieser Arbeit berichteten experimentellen Beobachtungen und der minimale Charakter ihrer mechanischen Erklärung ermöglichen die Entwicklung eines Überwachungsprotokolls, um das Auftreten katastrophaler Verhaltensweisen in großen Menschenmengen besser vorherzusagen. Diese Ergebnisse wurden in der Zeitschrift Nature veröffentlicht.
Referenz:
Emergence of collective oscillations in massive human crowds,
François Gu, Benjamin Guiselin, Nicolas Bain, Iker Zuriguel & Denis Bartolo, Nature, veröffentlicht am 5. Februar 2025.
Doi: 10.1038/s41586-024-08514-6
Open-Access-Archiv: HAL