Ende des Irrationalen: Mathematiker löst 200 Jahre altes Problem 📐
Veröffentlicht von Cédric,
Autor des Artikels: Cédric DEPOND
Quelle: The American Mathematical Monthly
Andere Sprachen: FR, EN, ES, PT
Autor des Artikels: Cédric DEPOND
Quelle: The American Mathematical Monthly
Andere Sprachen: FR, EN, ES, PT
Dieser Fortschritt, veröffentlicht in The American Mathematical Monthly, stellt seit dem 19. Jahrhundert etablierte algebraische Prinzipien in Frage. Durch die Nutzung kombinatorischer Sequenzen eröffnet er unerwartete Perspektiven für reine und angewandte Mathematik.
Die historische Sackgasse der Polynome höheren Grades
Polynomgleichungen wie x² + 5x + 6 = 0 werden seit der Antike gelöst. Und sie sind überall zu finden, etwa bei der Berechnung von Umlaufbahnen, Wettervorhersagen oder in der Computerkryptographie! Ab dem fünften Grad (jenseits von x⁴) wurden sie jedoch unlösbar, da sie Zahlen wie √2 oder π erfordern, deren Dezimalstellen nie enden. Évariste Galois hatte 1832 die Unmöglichkeit einer allgemeinen Radikallösung bewiesen, was Mathematiker zu numerischen Näherungen zwang.
Norman Wildberger von der University of New South Wales lehnt diese Beschränkung ab. Seiner Ansicht nach führt die Verwendung irrationaler Zahlen wie √2 oder π zu künstlichen Komplexitäten. Diese Zahlen, die unendlich viele Dezimalstellen benötigen, sind seiner Meinung nach "in der Praxis unberechenbar". Seine Lösung? Sie zu ignorieren.
Tatsächlich vermeidet seine Methode diese Fallstricke durch die Verwendung von Potenzreihen, polynomialen Erweiterungen mit potenziell unendlichen Termen. Getestet an einer historischen kubischen Gleichung, lieferte sie präzise Ergebnisse ohne Radikale.
Der Schlüssel: Geodätische Zahlen
Die Innovation basiert auf einer Verallgemeinerung der Catalan-Zahlen, einer kombinatorischen Folge, die angibt, wie ein Polygon in Dreiecke zerlegt werden kann. Wildberger und sein Kollege Dean Rubine haben diese Logik auf höhere Dimensionen erweitert und eine Struktur namens Geode geschaffen.
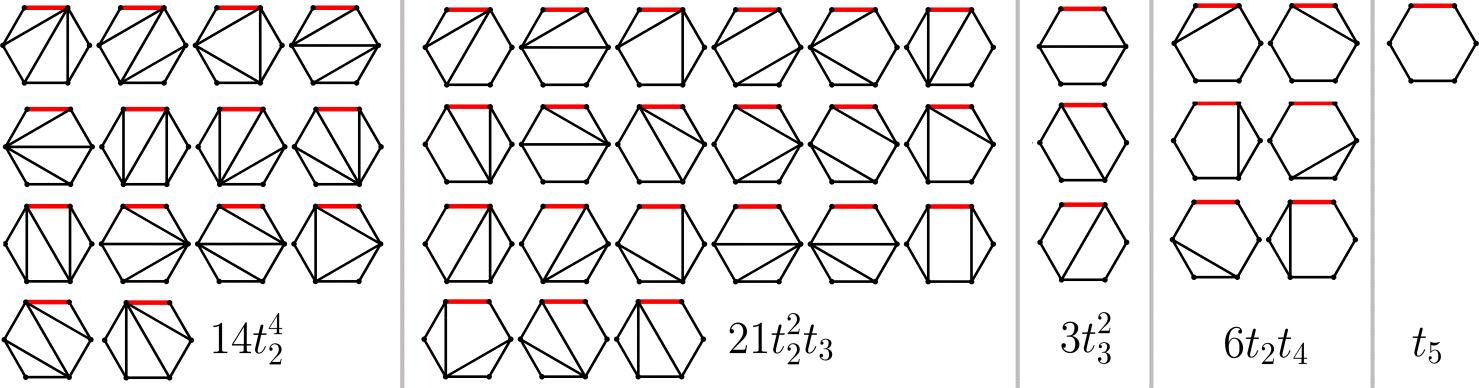
Darstellung mit Geode.
Diese neuen Zahlen ermöglichen die Lösung komplexer Gleichungen durch die Nutzung mehrdimensionaler geometrischer Muster. Ihr rein algebraischer Ansatz umgeht traditionelle Näherungen. Er könnte Algorithmen in der Informatik oder biologischen Modellierung optimieren.
Das Ergebnis? Sogar x⁵ wird lösbar! Getestet an einer Gleichung aus dem 17. Jahrhundert, lieferte seine Technik präzise Ergebnisse... ohne jemals unendliche Zahlen zu verwenden. Geode eröffnet auch ein unerforschtes Forschungsfeld. Konkrete Anwendungen sind denkbar, wie die Verbesserung von Bahnberechnungen oder Datenkompression.